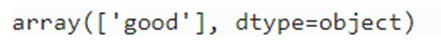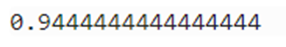機械学習入門：動かして学ぶ、機械学習のキソ(分類問題編)

※本記事はOracleの下記Meetup「Oracle Big Data Jam Session」で実施予定の内容です。

※本ハンズオンの内容は事前に下記セットアップが完了していることを前提にしていますのでご参加いただける方々は必ず下記ガイドの手順を実行ください。

※本記事の内容は以下の動画でも公開しておりますのでよろしければご参照ください。

本記事の対象者

• これから機械学習を利用した開発をしていきたい方
• 機械学習のトレンド技術を知りたい方
• なるべく初歩的な内容から学習したい方

前回の下記記事では、そもそも機械学習とは？というところから、アメリカボストンの住宅情報データを使い、回帰問題のシンプルなコードを概説しました。

本記事では、回帰問題同様、ビジネスの場でよく利用される分類問題のサンプルコードを取り上げたいと思います。前回同様、極めてシンプルなコードを学習することで、機械学習の典型的なワークフローや、コードの骨格をぼんやりとでも理解することが目標です。

データセットと分析シナリオ

今回の分類分析では様々な銘柄のワインに含まれる各成分を数値データとしてまとめたデータセットを利用します。各ワインに含まれる、アコール、リンゴ酸、マグネシウムなどの含有率や色の濃さ、吸光度など、ワインの品質に影響するであろう項目がまとめられたデータセットです。過去の記事(回帰分析による不動産価格の予測)と同じように、このデータセットを図にしてみると以下のようになり、青色の13個の特徴量と赤色の特徴量との関係を学習させ、予測モデルを構築します。赤色の特徴量は0, 1, 2の3つの値が記録されていることがわかります。このデータセット分類問題として利用する場合、各ワインの成分の値の組み合わせによって、そのワインがグループ0、1、2のどのグループに属するべきかという問題に応用することができます。仮に、この赤色の特徴量をワインの品質と見立てて、グループ0はgood、グループ1はbetter、グループ2はbestと定義すると、これは立派な「ワインの品質を予測するモデル」を作るデータセットになります。

念のため、本データセットの特徴量の意味を下記に記しておきますが、本ハンズオンの中では、単にワインの成分にはいろいろあってそれが並んでいるだなというレベルの理解で問題ありません。

• Alcohol（アルコール）
• Malic acid（リンゴ酸）
• Ash（無機成分）
• Alcalinity of ash（無機成分によるアルカリ度）
• Magnesium（マグネシウム）
• Total phenols（総フェノール類）
• Flavanoids（フラボノイド）
• Nonflavanoid phenols（非フラボノイド芳香族）
• Proanthocyanins（プロアントシアニン）
• Color intensity（色の濃さ）
• Hue（色相）
• OD280/OD315 of diluted wines（ワイン溶液の280 と 315nm の吸光度の比）
• Proline（プロリン）

過去の記事(回帰分析による不動産価格の予測)を読んでいただけた方は、回帰も分類も基本的な考え方はあまり変わらないじゃない？と気付かれた方も多いと思います。全くその通り、なぜなら回帰も分類も同じ教師あり学習とよんでいるタイプの学習手法だからです。

余談になりますが、このようなモデルを使うと、個人の好みを登録しておくと、世界中の様々なワインがレコメンドできたり、好みのワインが似ている人の好きなワインを参照できたり、といろいろなサービスが思いつきますね。また正解ラベルを10段階評価方式にして回帰問題として学習させると、美味しいかどうかの単純分類ではなく、そのワインの評価は8点というようなレーティング方式にもできますね。

コードの概説

データセットと分析シナリオを理解したところで、実際のコードを見てゆきたいと思います。今回も機会学習のライブラリとしては基本となるscikit-learnを使います。このライブラリには多種多様なデータセットが含まれており、上記のワインデータも実はその一つです。そのため下記のような単純なコードで簡単にデータがロードできます。 (※実システムでは、RDBやNoSQL系のデータストア、データレイクなど多種多様なデータストアに接続し、そこに貯められているデータを変換しながら、学習用のデータセットをトライアンドエラーで何度も作り直すという大変な作業を行います。)

まずはデータセットのロードです。

from sklearn.datasets import load_wine
data_wine = load_wine()

次に、ロードされたデータを確認しつつ、簡単な前処理を行います。先ほど、ロードしたデータをpandasのデータフレームに変換します。こうすることでpandasの便利なデータ処理関数を利用してデータの前処理や成形を行うことができます。またデータの前処理ではデータセット全体に処理を施したり、データセットの説明変数(データセットの青色の部分)のみ、もしくは目的変数(赤色の部分)のみに対して行う場合があります。その際、説明変数のデータフレームの変数名はX、目的変数の変数名はyとするのが慣例です。つまりXとyの関係を学習し、予測モデルy(X)を構築するというイメージです。

まずはロードしたデータdata_wineから目的変数と特徴量の名前を抜き出して説明変数用のデータフレームを作成します。

import pandas as pd
X = pd.DataFrame(data_wine["data"],columns=data_wine["feature_names"])

shape関数でデータフレームXの行数と列数を確認します。

X.shape

headでどのようなデータフレームができたかを確認してみます。

X.head()

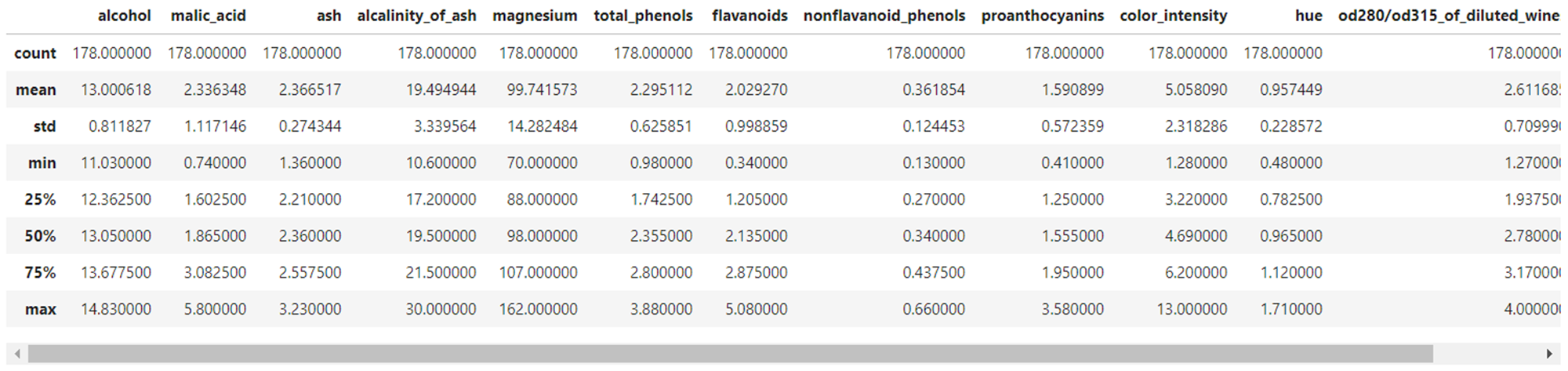
describeを使って全特徴量の統計値の概要を確認してみましょう。出力の各項目の意味は下記の通りです。一目で各特徴量の分布を比較できる非常に便利な関数です。株式投資をされている方であれば、株価チャートから確認できる見慣れた統計情報かと思います。

• count: 個数
• mean: 算術平均
• std: 標準偏差
• min: 最小値
• max: 最大値
• 50%: 中央値
• 25%: 1/4分位数
• 75%: 3/4分位数

X.describe()

過去の記事(回帰分析による不動産価格の予測)では各特徴量同士の相関関係を確認していました。説明変数同士で相関関係が強い特徴量を学習データに含めてしまうと多重共線性という症状が発生し、予測モデルの精度に悪影響を及ぼすことがあるため、原則、そのような特徴量は一つに絞ります。ですが、本サンプルコードは回帰分析ではなく分類分析ですので気にする必要はありませんが、データ把握の観点から相関関係を確認しておきましょう。

各特徴量の相関関係をチャート化するために、seabornをインポートし、ヒートマップとして出力すると、非常にわかりやすいです。このヒートマップの見方は過去の記事(回帰分析による不動産価格の予測)をご参照ください。

import seaborn as sns 
corr_matrix = X.corr().round(2)
sns.heatmap(data=corr_matrix, annot=True)

説明変数のデータフレームについてはここまでにして、目的変数の簡単な前処理を行いたいと思います。

まずは、説明変数の時と同様に、ロードしたデータdata_wineから今度は目的変数を抜き出し、pandasのデータフレームを作成します。すでに説明したとおり、目的変数の変数名は慣例に倣い、yとしておきましょう。headで確認すると目的変数だけのデータフレームが作成できていることがわかります。

import pandas as pd
y = pd.DataFrame(data_wine["target"],columns=["target"])
y.head()

headでは指定した行数だけしか確認できないので、sampleで作成したデータフレームから20個ほどデータをサンプリングしてみると、0, 1, 2の三つの値が記録されていることが確認できます。

y.sample(20)

人間がこのデータを見ると、0, 1, 2の3つのカテゴリに分類されていることは想像できますが、この0, 1, 2という値は数値としての意味を持つため、分類問題には適していません。したがって、この整数値の変数をカテゴリカル変数に変換する必要があります。今回の分析シナリオは「ワインの品質を予測する」というものですので、この0, 1, 2をgood, better, bestに変換します。

y = y.replace({0:'good', 1:'better', 2:'best'})

先ほどと同じように、sampleでデータフレームを表示するとちゃんと変換されていることがわかります。

y.sample(20)

ここで、これまで作成したデータフレームがどういうものかをまとめて確認しておきましょう。 データフレームは下記2つを作成しました。

• X(説明変数): ワインの成分をまとめたデータフレーム
• y(目的変数): ワインの品質をgood, better, bestの3段階で記録したデータフレーム

そして、ここから、この2つのデータフレームを更に、学習用データと評価用データに分割します。学習用データはその名の通り、予測モデルを作るために使うデータです。そして、予測モデルを作った後に、そのモデルでどの程度の精度がでるのかを評価するためのデータが評価用データです。モデルの評価は、そのモデルにとって未知のデータで実施する必要があるため、学習用データと評価用データに分割します。つまり、最終的には以下の4つのデータフレームが出来上がります。

データフレーム X(説明変数)を下記2つに分割

• X_train(説明変数)：y_trainと共に、学習用データとして利用
• X_test(説明変数):y_testと共に、評価用データとして利用

データフレーム y(目的変数)を下記2つに分割

• y_train(目的変数)：X_trainと共に、学習用データとして利用
• y_test(目的変数):y_testと共に、評価用データとして利用

分割はtrain_test_splitという関数を使います。引数のtest_sizeで、評価用に全体の何パーセントのデータを割り当てるかを指定します。仮に0.3を指定すると、評価用に全体の30%のデータが使われ、残り70%データが学習用に使われるということになります。つまり、全体の70%のデータで学習した予測モデルを、残り30%のデータで答え合わせをするというイメージです。また、ここでは省略していますが、train_test_splitにはshuffleというデフォルト引数があり、これがTrueになっているとデータを分割する前にランダムに並び替えを行ないます。乱数を使ってランダムに並び替えた後にデータ分割をするのですが、その乱数のシードを引数randome_stateで固定するというイメージです。つまり、randome_stateの値が同じであれば何度実行しても必ず同じデータセットを作ることができます。今回は意識する必要はありませんが、複数の乱数シードをランダムに選んで複数回学習と評価を行い、行った結果を統計処理したいなどの場合に有効です。

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

分割した各データフレームの行数と列数をshape関数で確認してみます。

X_train.shape

X_test.shape

y_train.shape

y_test.shape

もともと178行あったデータは学習用データ(70%)の124行と、評価用データの54行に分割されたことがわかります。また説明変数のデータフレームはX_train、X_testともに13列、目的変数のデータフレームであるy_train、y_testともに1列であることがわかります。

これで、学習用データと評価用データが出来上がりました。もうすぐにでも機会学習の統計処理にかけられる状態にありますが、実際の分析の現場ではそうはいきません。今回使用しているデータセットはscikit-learnに付属しているデータセットです。分類問題を体感するためのデータセットですから、当然、無難に分類はできるようなデータの分布になっているわけです。ですが実ビジネスで発生するデータはそうはいかないと思います。従って、実際に長時間の学習処理を実行する前に、「このデータは本当に分類できそうなのか？」という当たりをつけておきたいということがあります。ということで、非常に簡単ではありますがその「当たりをつける」ためのデータ探索をしてみたいと思います。いわゆるExploratory data analysis(探索的データ解析)とよばれているものです。

まずは、いったん、X_trainとy_trainを合体させたデータフレームをtrainという名前で作成します。

train = pd.concat([X_train,y_train],axis=1,sort=False)

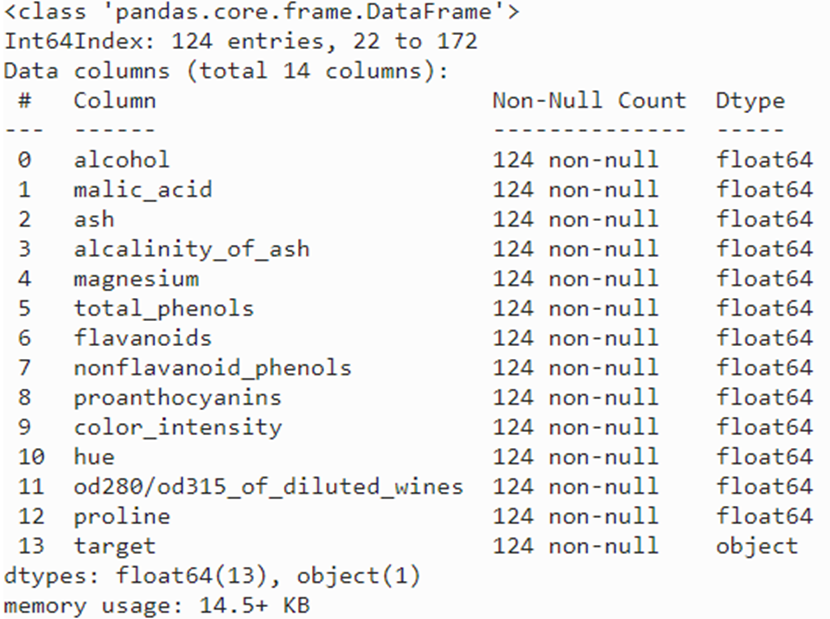
infoでtrainの概要を確認します。

train.info()

124行のデータで、0から12までの13個全ての説明変数のデータ型はfloat型、そして、1つの目的変数があることが確認できます。 つまり、このデータセットは全ての特徴量が浮動小数点数で構成されているので、各値の分布状態を確認することで分類ができそうか当たりがつけられそうです。

まずは3つのクラス(good/better/best)の平均値を確認してみましょう。groupbyでソートし、meanで平均値を計算します。

train.groupby("target").mean()

そうすると、flavanoids、color_intensity、prolineあたりの特徴量におけるクラスごとの差は他の特徴量と比べてかなり差あることが分かります。

ということでこの3つだけを抜き出してみます。 平均値の差が最小と最大で、flavanoidsは380%、color_intensityは250%、prolineは210%もの差になるので、各クラスの要素の分布はかなり分離状態にある可能性が期待できます。

train.groupby("target").mean()[["flavanoids","color_intensity","proline"]]

この3つの特徴量の分布を各クラスごとにseabornと呼んでいるライブラリを使ってボックスプロット(箱ひげ図)でチャート化してみます。

import seaborn as sns 
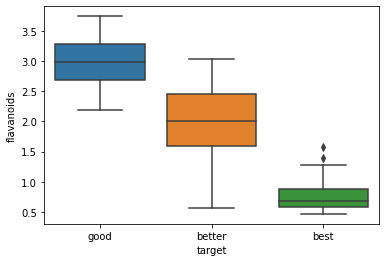
sns.boxplot(x='target', y='flavanoids', data=train)

flavanoidsはクラス間で最も差が大きかった特徴量です。予想通り、各クラス間の全体範囲の重なりはあるものの、四分位範囲(箱の部分)の重なりは全くないので全てのクラスをきれいに分離できそうです。

次に、color_intensityをチャート化してみます。

import seaborn as sns 
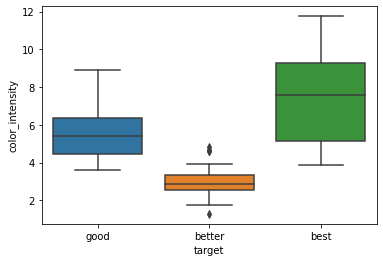
sns.boxplot(x='target', y='color_intensity', data=train)

同じく四分位範囲を確認すると、他のクラスとの重なりがないbetterはきれいに分離できそうです。

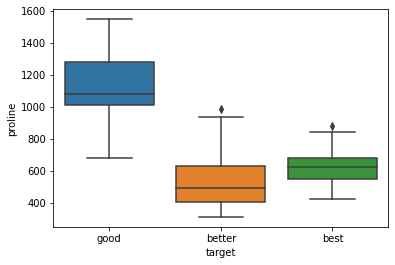
次にprolineをチャート化します。

import seaborn as sns 
sns.boxplot(x='target', y='proline', data=train)

同じく四分位範囲を確認すると、他のクラスとの重なりがないgoodはきれいに分離できそうです。

箱ひげ図は、データの分布について、最小値、最大値、四分位数、四分位範囲などで値を正確に把握することができますが、箱の中でどのような分布にはっているかはわかりません。ですので、次は、散布図でチャート化し、箱ひげ図の箱の中のデータ分布を確認したいと思います。

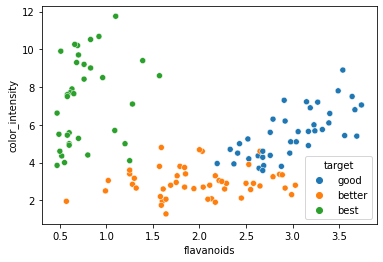
sns.scatterplot( x='flavanoids', y='color_intensity',hue="target", data=train)

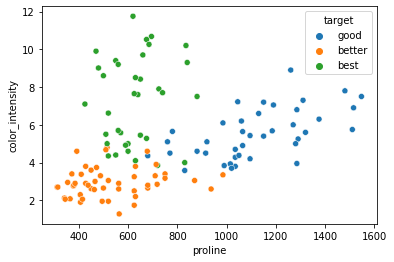
sns.scatterplot( x='proline', y='color_intensity',hue="target", data=train)

sns.scatterplot( x='proline', y='flavanoids',hue="target", data=train)

いずれも重なりはあまり多くなく、分離しやすいデータだということが直感的にわかると思います。逆に、各要素のデータ分布が入り組んで重なっていると分離しにくいということになります。

ここまでの作業で、機会学習にかけるデータセットの作成が完了し、そのデータの分布から、うまく分類できそうだということがわかりましたので、このデータセットを機会学習にかけるステップに入ります。分類問題で利用できるアルゴリズムは下記にリストしたように多々あり、データの種別や量、分布の度合、分類クラス数など、その他様々な条件からアルゴリズムを選択します。

• 決定木(Decision Tree)
• 一般化線形モデル(GLM)
• 単純ベイズ(Naive Bayes)
• ランダム・フォレスト(Random Forest)
• サポート・ベクター・マシン(SVM)
• 明示的セマンティック分析(ESA)
• ニューラルネットワーク(NN)
• 勾配ブースティング木(GBDT)

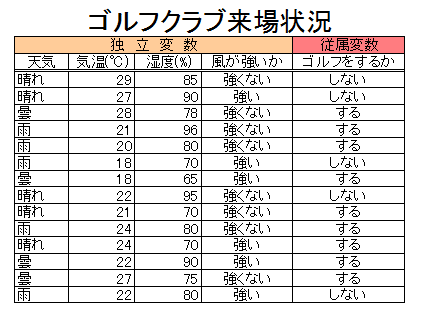
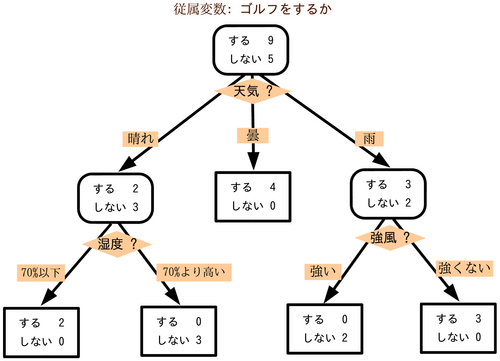
ここでは、まずは、非常にわかりやすい決定木(Decision Tree)と呼んでいるアルゴリズムを使ってみたいと思います。 決定木分析とは、何らかの意思決定の際に、その決定に影響を与えている「条件」の内容(値など)によって、最終的な意思決定がどのようなパターンになるかを導き出すアルゴリズムです。 下図のように、「意思決定の内容」は、その条件がとりえる「値」によってツリー構造に分岐するわけですが、この複数条件の分岐点と、その組み合わせを統計的に導き出す計算をするのが決定木です。つまり、上述した、決定に影響を与えている「条件」が説明変数(従属変数)となり、「意思決定の内容」が目的変数(独立変数)となります。

ゴルフに行くか行かないかの意思決定の決定木

出典 wikipedia https://ja.wikipedia.org/wiki/%E6%B1%BA%E5%AE%9A%E6%9C%A8

そして、決定木だけでなく、機械学習で使われるアルゴリズムはほぼ全てにおいてハイパーパラメータというパラメータを持っています。これらの値を何にするかで、学習にかかる時間や最終的にできあがる予測モデルの精度が変わってきます。

決定木アルゴリズムのハイパーパラメータ　

• criterion 分岐点の基準値の算出手法
• max_depth　決定木の深さの最大値
• min_samples_split　サンプルを枝に分割する数の最小値
• min_samples_leaf　サンプル1つが属する葉の数の最小値
• min_weight_fraction_leaf　1つの葉に属する必要のあるサンプルの割合の最小値
• max_leaf_nodes　作成する葉の数の最大値(指定した場合max_depthは無効化）
• max_features　最適な分割を探索する際に用いる特徴数の最大値
• class_weight　クラスの数に偏りがある場合に、クラスごとの重みを調整

ハイパーパラメータの詳細はやデフォルト値は下記scikit-learnのマニュアルをご確認ください。 https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html

決定木については後ほどもう少し詳しく触れますので、現状この程度の理解で十分です。

それでは学習に利用するアルゴリズムを決定木として定義してゆきましょう。ハイパーパラメータはmax_depthだけを指定、その他はデフォルト値でdecisiontree_clfという名前でモデルを定義します。

※時間に余裕がある方は後ほど、いろんなパラメータを試してみてください。例えば、max_depthの値を1や2にして今回の結果と比較してみるのもいいと思います。

from sklearn.tree import DecisionTreeClassifier
decisiontree_clf = DecisionTreeClassifier(max_depth=3)

アルゴリズムが定義できたので、fit関数でdecisiontree_clfを学習させます。

decisiontree_clf.fit(X_train, y_train)

これで学習が完了し、予測モデルが構築できましたので、実際に予測処理を行ってみたいと思います。予測するデータは学習時に利用しなかった X_test から下記のように一行抜き出したデータで予測をします。

X_pred = X_test.iloc[0:1]
X_pred

予測をする前に、このデータ(ワイン)の正解ラベルを確認しておきましょう。

y_pred = y_test.iloc[0:1]
y_pred

上記のように正解ラベルはgood、つまりこのワインの品質はgoodであることがわかります。実際にgoodと予測できることを期待しつつ、predict関数で予測実行します。

decisiontree_clf.predict(X_pred)

正解ラベル同様、ちゃんとgoodに分類できたことが確認できました。

上記は一つのワインデータだけを予測しましたが、X_testにリストされているすべてのワインの品質の予測予測結果を、正解ラベルと照合し、どの程度の正解率になったかを計算することで、このモデルの「確からしさ」の各種の指標値で把握することができます。

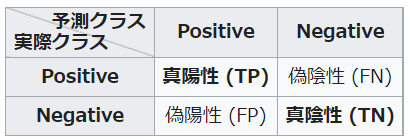
回帰問題同様に、分類問題も、モデルの確からしさを評価する手法はおおよそ決まっています。下記は分類クラスが2つ(PositiveとNegative)の例ですが。評価データの予測結果から、まずは混同行列と呼ばれているものを作成します。

各マスの意味は下記の通りです。

予測結果が正解だったもののうち、

• Positiveで正解だったものをTrue Positive(TP)
• Negativeで正解だったものをTrue Negative(TN)

予測結果が不正解だったもののうち、

• Positiveで不正解だったものをFalse Positive(FP)
• Negativeで不正解だったものをFalse Negative(FN)

そして、混同行列から、下記5つの指標を計算し、モデルの確からしさを判断します。

• 正解率(accuracy)：予測モデルがテストデータを正しく推論できた割合
  

• 精度(precision)：予測モデルがpositiveと判断した時の信用度を示す指標
  

• 再現率(recall)/真陽性率(true positive rate: TPR)：positiveのデータ全体の内、予測モデルがどれぐらい正しくpositiveと推論できたかを示す指標
  

• 偽陽性率 (false positive rate: FPR)：negativeデータ全体の内、予測モデルがどれくらい誤ってpositiveと推論してしまったかを表す指標
  

• F値(F-measure)：精度(precision)と再現率(recall)の調和平均
  

上記のようにモデルの評価にはたくさんの指標を確認する必要がありますが、ここでは一旦、一番わかりやすい、正解率(accuracy)のみを確認しておきましょう。

from sklearn.metrics import accuracy_score, roc_auc_score, confusion_matrix, precision_score, recall_score

y_pred_score = decisiontree_clf.predict(X_test)
accuracy_score(y_test, y_pred_score)

結果、このモデルの精度は94%であることがわかりました。100回予測すると94回は正解が出せるということになります。

最後に、このモデルがどのような木構造をしているのかを確認しておきましょう。作られたモデルを理解しておくことは非常に重要な作業で、昨今、急速に認知が広まっている分野です。モデルを理解しておくことでモデルの不備を見つけやすくなりますし、予測結果のブラックボックス化を防ぎ、なぜそのような結果になったかを説明できるようになります。

import matplotlib.pyplot as plt
from sklearn import tree

plt.figure(figsize=(20,8))
tree.plot_tree(decisiontree_clf,feature_names=data_wine.feature_names,filled=True,proportion=True,fontsize=8)
plt.show()

上記の木構造は下記のように読み解きます。

• ノード
  箱がツリー構造で表示されていることがわかります。この箱をノードと呼んでおり、そのノードの色でクラスが表現されています。

• 条件の分岐点
  箱には特徴量と特徴量の分岐点となる値が不等号で記されていることがわかります。これは該当特徴量の値が表示された値以下だったときと、その値より大きい場合で次の層に分岐しているということです。

• gini(ジニ係数)
  giniという表示はジニ係数と呼んでいるものです。ジニ係数とは不純度を計る係数となり、値が１に近づくほど不純度が高く、0に近いほど不純度が低いということになります。決定木でいうと、「不純度が高い状態」つまり「ジニ係数の値が高い状態」とは、一つのノード内に複数クラスの要素が分布している状態のことを言います。決定木の計算は、ジニ係数が0になり、ノードが一つのクラスに確定するまで計算が続きます。従って、一つのノード内に複数のクラス要素が分布している状態は「不純度が高い」ということになります。

• Value
  逆に言うと、決定木の計算は、ノード内のジニ係数が0になり、ノードのクラスが一つに収束するまでの、各特徴量の分岐点の値を算出するアルゴリズムだといえます。そのノードが一つのクラスに収束しているのか、それともまだ複数クラスの要素が含まれているのかはvalueの値で確認することができます。本サンプルコードは3つのクラス(good/better/best)のどれかに収束することが目的になりますのでvalueにはこの3つのクラスに相当する3つの値が表示されています。一つの値が1.0になっている場合はその一つのクラスに収束していることになります。

• Samles
  そして、samplesで表示されている値が全データの何パーセントがそのノードに分類されているかということを表しています。基本的には上から数えて、木の深さが深くなるほど、ジニ係数は小さく収束する傾向にあり、また同じ深さのノードのsamplesの値の合計は100%になり、ノード内のvalueの合計は1.0になります。

従って、新しいデータを、このツリー構造の分岐点の値の通りに辿っていくと、どのクラスに属するかが予測できるということになります。

以上が決定木アルゴリズムによる分類問題のハンズオンでした。

さいごに

今回は「機械学習のコードの骨格」を理解することが目標でしたので、「アルゴリズムの可読性」を重視し、決定木を題材として選択しました。ですが、実はこのアルゴリズムが実際の分析の現場で使われることはまずありません。実ビジネスで生成されるデータの分布はもっと複雑でこのような単純なアルゴリズムでは精度がでないからです。ただし、この知識が無駄になることはありません。決定木の上位互換にランダムフォレストや勾配ブースティング木といった、決定木と同じツリー系のアルゴリズムがあります。これらは分類問題にも回帰問題にも利用でき、かつ高い精度が期待できるアルゴリズムなので広く利用されています。ですので、今後の学習ステップとしては、今回と同じワインのデータセットを利用し、

1. アルゴリズムを決定木からランダムフォレストに変更したコードを学習
2. 最適なハイパーパラメータの選定を自動化するGridSearchCVを追加したコードを学習
3. 最適なアルゴリズムの選定を自動化するauto sklearnのコードを学習

という流れで学習するとよいかと思われます。その際は、上記3つのコードに相当する下記コードをご参考にされてください。
(※上述した、train_test_splitでX_train, y_train, X_test, y_test作成後以降の追加のコードを下記に掲載しています。)

アルゴリズムを決定木からランダムフォレストに変更したコード

from sklearn import ensemble

# ランダムフォレストの定義
randomforest_clf = ensemble.RandomForestClassifier(max_depth=3)

# 学習実行
randomforest_clf.fit(X_train, y_train)

# 正解率の確認
y_pred = randomforest_clf.predict(X_test)
accuracy_score(y_test,y_pred)

# ランダムフォレストの可視化
!pip install dtreeviz

from dtreeviz.trees import dtreeviz

X=data_wine.data
y=data_wine.target

estimators = randomforest_clf.estimators_
viz = dtreeviz(
    estimators[1],X,y,
    target_name='wine quality',
    feature_names=data_wine.feature_names,
    class_names=list(data_wine.target_names),
) 

display(viz)

最適なハイパーパラメータの選定を自動化するGridSearchCVを追加したコード

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV

# 各ハイパーパラメータの値のパターンの定義
param_grid = {"max_depth":[1,2,3,5,7], "n_estimators":[100,200,500],"min_samples_split":[2,3,5,7] }

# アルゴリズムとグリッドサーチを定義
randomforest_gs_clf = GridSearchCV(estimator=RandomForestClassifier(random_state=0),
                 param_grid = param_grid,   
                 scoring="accuracy",  
                 cv = 5,              
                 n_jobs = -1)

# 学習実行
randomforest_gs_clf.fit(X_train,y_train["target"].values)

# ベストなハイパーパラメータの値の組み合わせを確認
print("Best Model Parameter: ",randomforest_gs_clf.best_params_)

# ベストなハイパーパラメータの値を組み込んだモデルを定義
randomforest_gs_clf_best = randomforest_gs_clf.best_estimator_ #best estimator

# 正解率の確認
y_pred = randomforest_gs_clf_best.predict(X_test)
accuracy_score(y_test,y_pred)

最適なアルゴリズムの選定を自動化するauto sklearnのコード

# scikit-learnのバージョンアップグレードとauto-sklearnのインストール
!pip install scikit-learn==0.24.0
!pip install auto-sklearn

from sklearn import datasets, metrics, model_selection, preprocessing, pipeline
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
import autosklearn.classification

# auto sklearnで分類アルゴリズムを定義
auto_model = autosklearn.classification.AutoSklearnClassifier(time_left_for_this_task=30, ensemble_size=3)

%%capture

# 学習開始
auto_model.fit(X_train, y_train)

# 混同行列のチャート化
predicted = auto_model.predict(X_test)
confusion_matrix = pd.DataFrame(metrics.confusion_matrix(y_test, predicted))
confusion_matrix

# 精度メトリックの確認
print("accuracy: {:.3f}".format(metrics.accuracy_score(y_test, predicted)))
print("precision: {:.3f}".format(metrics.precision_score(y_test, predicted, average='weighted')))
print("recall: {:.3f}".format(metrics.recall_score(y_test, predicted, average='weighted')))
print("f1 score: {:.3f}".format(metrics.f1_score(y_test, predicted, average='weighted')))