「Rで学ぶベイズ統計学入門」の例題で勉強したことを紹介していくことにします。今回の例題はこちら。
ボブは自分に超感覚的知覚があると主張している。
事実かどうかを確かめるため、4枚のカードから1枚選んで図柄を言い当てる実験をした。
10回実験を繰り返し、正解は6回、不正解は4回であった。
ボブに超感覚的知覚などないとする事後確率は?
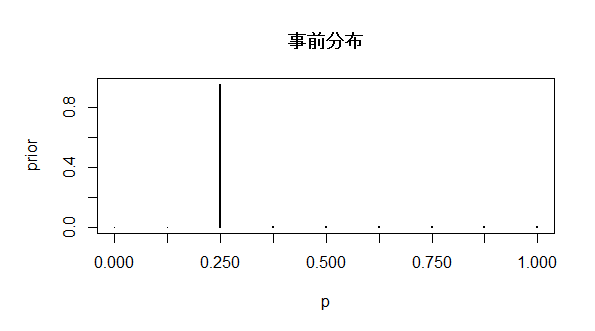
ボブが正解する確率pの事前分布には以下の離散分布をおくことにしています。
p <- seq(0, 1, length.out = 9)
prior <- c(0.001, 0.001, 0.950, 0.008, 0.008, 0.008, 0.008, 0.008, 0.008)
plot(p, prior, type = "h", lwd = 2)
出題者はボブをかなり妄想癖のある人間だと思っているようです。事前確率は「特殊能力なし」(p<=0.25)が97%という冷ややかな対応です。ところが蓋を開けると、1/4の確率のところを6割も当ててしまうという、ちょっと焦る状況になりました。そこで、これが決定的な証拠になるのかどうか、統計に詳しいあなたに尋ねてきた、というわけです。
離散事前分布から事後分布を計算する
さて復習ですが、ベイズの定理は
$$事後確率 \propto 尤度 \times 事前確率$$
となります。独立試行を繰り返して何回成功するかという問題なので、尤度関数は二項分布を使います。今回は事前確率および事後確率が離散分布なので、事後確率は足し合わせると1になる条件を満たす必要があります。これは、尤度と事前確率をかけた後に、単純に合計で割ればOKです。
posterior <- dbinom(6, 10, p) * prior
posterior <- posterior / sum(posterior) # 合計で割って規準化する
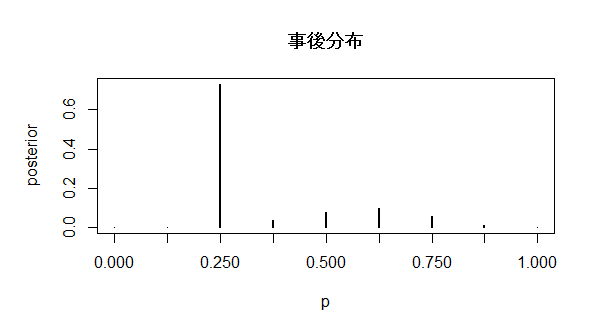
plot(p, posterior, type = "h", lwd = 2, xaxp = c(0, 1, 8),
main = "事後分布")
p=0.675あたりが若干盛り上がってきましたが、依然としてp=0.25が有力です。p>0.25を特殊能力ありということにすると、なし(FALSE)およびあり(TRUE)の事後確率は、
tapply(posterior, p > 0.25, sum)
# FALSE TRUE
# 0.730495 0.269505
特殊能力なしが事後確率73%と、ボブの健闘にも関わらず、あまり信じてもらえませんでした。やはり「ボブ=妄想の事前確率97%」はハードルが高すぎか・・・
別の事前分布を仮定した場合
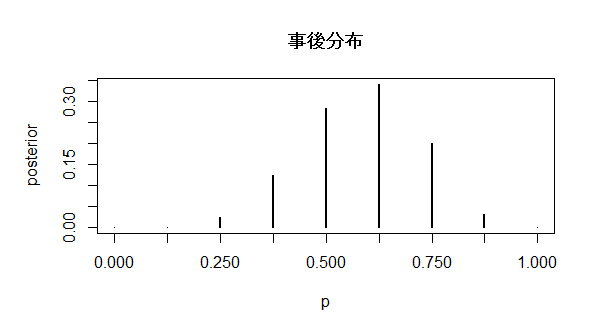
ちなみに、事前分布に離散一様分布を仮定してみると以下のようになりました。
prior <- rep(1, 9) / 9
posterior <- dbinom(6, 10, p) * prior
posterior <- posterior / sum(posterior)
plot(p, posterior, type = "h", lwd = 2, xaxp = c(0, 1, 8),
main = "事後分布")
tapply(posterior, p > 0.25, sum)
# FALSE TRUE
# 0.02294642 0.97705358
「特殊能力あり」が98%と高い支持を得ています。
ちなみに、この結果はbinom.testで母比率検定をやったときのp値が2%という結果とほぼほぼ一致します。
binom.test(6, 10, 0.25, alternative = "greater")
#
# Exact binomial test
#
# data: 6 and 10
# number of successes = 6, number of trials = 10, p-value = 0.01973
# alternative hypothesis: true probability of success is greater than 0.25
# 95 percent confidence interval:
# 0.3035372 1.0000000
# sample estimates:
# probability of success
# 0.6
#
まとめ
事前分布をどうおくかによって結果がまったく変わってくることが分かりました。今回のケースが一様事前分布(超なんとか能力に対して「あるのかもしれないしないのかもしれない」みたいなフラットな立場)がいいのかどうかは分かりません。しかし、「事前確率で97%嘘つきだから、その程度じゃ証拠になんねーよ」というのはボブちょっと可哀想なのでは?