前回に続いて「Rで学ぶベイズ統計学入門」からの例題です。今回は離散一様分布を使った問題になります。
ある町のタクシーには1からNまでの番号が振られている。
待っている間に5台のタクシーが通り過ぎたが、それぞれ43, 24, 100, 35, 85という番号がついていた。
どの番号のタクシーが現れる確率も同じであり、タクシーの台数は200台を越えないことがわかっている。
この町のタクシーの台数の事後平均および150台を越える確率を求めよ。
タクシーの番号から台数を推定するというちょっと面白い問題です。
尤度関数は一様分布
タクシーには1から順番に番号がついているので、番号の最大値Nがこの町のタクシーの台数になります。現れるタクシーの番号は1からNまでどの値をとる確率も同じである離散一様分布に従うことになります。離散一様分布の確率関数は$1/N$になります。したがって、$y_1,..,y_n$のn台のタクシーを観測したとき尤度は次のようになります。
$$
尤度 = \frac{1}{N^n} \hspace{10pt} ただし、yの最大値 \leq N \leq 200
$$
事前分布も一様分布 → 定数なので無視
Nの事前分布は1から200までのいずれの整数も同じ程度にあり得るので、離散一様分布$1/200$を仮定します。
事後分布は$尤度\times事前分布$に比例しますが、事前分布は$1/200$という定数なので比例定数として無視してよく、次のようになります。
$$
事後確率 \propto \frac{1}{N^n} \hspace{10pt} ただし、yの最大値 \leq N \leq 200
$$
今回のように一様事前分布を仮定した場合、事後分布の計算で事前分布は無視することができ、事後分布は尤度のみに比例することがわかりました。
では、ここまでの計算をやってみましょう。
# Nのとりうる範囲
N <- seq(1, 200, 1)
# 事前分布
prior <- rep(1 / 200, 200)
# 観測した5台のタクシー番号
y <- c(43, 24, 100, 35, 85)
# 観測数
n <- length(y)
# 尤度関数
likelihood <- (1 / N ^ n) * ((N >= max(y)) & (N <= 200))
# 事後分布
posterior <- likelihood * prior
posterior <- posterior / sum(posterior) # sum(posterior)で割って規格化
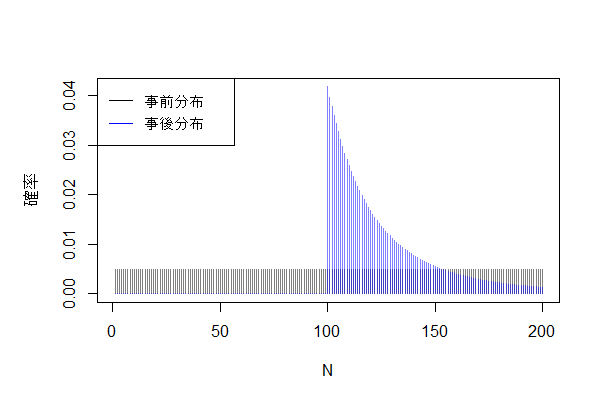
plot(N, prior, type = "h", col = rgb(0, 0, 0, alpha = 0.5),
ylim = c(0, max(posterior)), ylab = "確率")
segments(N, 0, N, posterior, col = rgb(0, 0, 1, alpha = 0.5))
legend("topleft", legend = c("事前分布", "事後分布"),
col = c("black", "blue"), lty = 1, cex = 0.8)
結果
事後分布は$N=100$で確率が最大となり、それ未満ではゼロ、100以上では指数的に減衰する形になりました。問題の解答は以下のようになりました。
# Nの事後平均
sum(N * posterior) # => [1] 123.9757
# Nが150を越える確率
sum(posterior[N > 150]) # => [1] 0.1388247
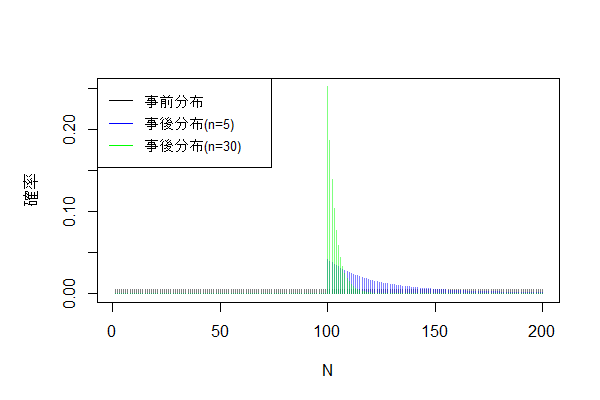
観測数がもっと増えるとどうなるか?
例題はこれで終わりですが、せっかくなのでもう少し考察してみたいと思います。もし、5台ではなく30台観測した中で$y_1,...,y_{30}$の最大番号が100だった場合、事後分布はどのような形になるでしょうか?
予想通り、$N=100$のあたりに集中した尖った形の分布になりました。事後平均および150を越える確率は、以下のようになります。たくさんのタクシーを目撃するほど、「もっと番号の大きいタクシーをまだ見ていない確率」が下がっていく様子がわかりました。
# Nの事後平均
sum(N * posterior) # => [1] 103.0787
# Nが150を越える確率
sum(posterior[N > 150]) # => [1] 6.153165e-06
台数の上限にが事前に分からなかったら?
今回の例題では、「タクシーの台数が200台を越えない」という事前情報がありました。もしこの情報がなかった場合、結果にどう影響するでしょうか?極端な話**「1つの町にタクシーが100万台も走ってることはさすがにあり得ない」**ということで、仮に、$N \leq 1000000$とすると最初の例題の答えはどうなるか計算してみたいと思います。
# Nのとりうる範囲(1から100万)
N <- seq(1, 1e+6, 1)
# 事前分布(100万分の1)
prior <- rep(1 / 1e+6, 1e+6)
# 観測した5台のタクシー番号
y <- c(43, 24, 100, 35, 85)
# 観測数
n <- length(y)
# 尤度関数
likelihood <- (1 / N ^ n) * ((N >= max(y)) & (N <= 1e+6))
# 事後分布
posterior <- likelihood * prior
posterior <- posterior / sum(posterior) # sum(posterior)で割って規格化
# Nの事後平均
sum(N * posterior) # => [1] 132.6711
# Nが150を越える確率
sum(posterior[N > 150]) # => [1] 0.1910587
最初の$N \leq 200$のときの計算とそれほど大きく変わらない結果になりました。理由は最初のグラフからも明白で、$N=200$の時点では確率がかなり減衰していて、$N > 400$とかになるともうほぼゼロになるからです。ですので、$N \leq 200$みたいな事前情報がない場合、事前分布のNの最大値は十分に大きく(たとえば500とかに)しておけば、それ以上は100万にしようと100億にしようと結果は変わらないということです。