Microsoft Qunatum Simulator を触ってみた #2

#はじめに
前回はMicosoftの量子シミュレータの導入について基礎編として紹介しました。
量子コンピュータ アドベントカレンダー 2017では、グローバーのアルゴリズムやショアのアルゴリズムなどを取り扱っているため、今回はこんなことに使える！という量子シミュレーションの応用編、分子構造シミュレーションを取り扱います。

素因数分解やデータベース検索など、古典コンピュータでは不可能とされていたもしくは遅かった計算を早くできることが量子コンピュータのメリットですが、一方で”量子”という名前がついていることから、量子化学のシミュレーションにも応用できるとして、化学・薬品メーカーからも注目を受けています。
汎用的なシナリオではなく万人受けする内容ではないと思いますが、こんなことにも使えるんだなと感じていただければ幸いです。（さらに、私は化学専攻出身ではないので、もし誤ったことを言っていたらご指摘いただけますと幸いです。）
もちろん上記に挙げた、グローバルのアルゴリズムやショアのアルゴリズムもサンプルコードとしてあるので、ぜひ触ってみてください。

#背景
分子構造シミュレーションのモチベーションとして、分子電子構造ハミルトニアンの最小エネルギー固有値すなわち”エネルギー”の計算があります。しかし、その解を得るための方程式は複雑極まりないため、パラメータ削減や次数下げを施し、近似解として求めます。
基底状態の波動関数は、分子軌道に基づいて指数関数的な数の状態にわたって重ね合わされる可能性が高いのですが、コンピュータのメモリ制限のために、取りうる複数解を制限しています。
しかしながら、量子コンピュータだと重ね合わせ状態を表現することができるため、複数な多対相関を含むことができます。
以上の背景から、これまで制限となって得られなかった分子構造が見られるのでないかと期待されています。
本サンプルコードは " Scalable Quantum Simulation of Molecular Energies "を参考にしています。

#目的
２つの水素原子が結合している水素分子に対して、結合の長さ $R$とエネルギー固有値をシミュレーションします。エネルギー固有値は離散的な値を取りますが、水素原子の場合、基底状態と第一励起状態とのGapは大きく、ほとんどが基底状態を取りうると考えられるので、基底状態のエネルギー固有値を求めることが目的となります。
量子計算に使用されるこのハミルトニアンは、核電荷Ziの集合と、対応するハミルトニアンが書かれたシステムN内の多電子で記述でき、
$$H = -\sum_i \frac{\nabla^2_{R_i}}{2M_i}-\sum_i \frac{\nabla^2_{r_i}}{2}-\sum_i \frac{Z_i}{|R_i-r_i|}+\sum_{i, j>i} \frac{Z_iZ_j}{|R_i-R_j|}+\sum_{i, j>i} \frac{1}{|r_i-r_j|}$$
ここで、$R_i$, $M_i$, $Z_i$はそれぞれ、核の位置座標、質量、電荷を表し、$r_i$は電子の位置を表します。
これらを実空間に配置し量子コンピュータで計算するために近似したものが以下の式となり、
$$H=g_o\mathbb{1}+g_1Z_o+g_2Z_1+g_3Z_0Z_1+g_4Y_0Y_1+g_5X_0X_1$$
となり、$g_i$は結合の長さ $R$ の関数として表すことできます。
この時、分子の波動関数は以下のようになります。
$$|\phi (\theta)> = e^{-i\theta X_0Y_1}|01>$$
この$|01>$は2量子ビットに対応することになります。
この時のエネルギー固有値は以下のように導けて、
$$E(\theta) =\sum_{\gamma}g_{\gamma}<\phi(\theta)|H|\phi(\theta)>$$
このエネルギー固有値を求めることになります。

#実装
##環境

• Windows OS
• Visual Studio 2017
  サンプルは前回同様、Githubから複製したサンプルを使い、[QsharpLibraries]>[samples]>[3.Simulation]>[H2SampleCmdLine]から利用できます。

##サンプルコード

qiita.rb

namespace Microsoft.Quantum.Samples.H2Simulation {
    open Microsoft.Quantum.Primitive;
    open Microsoft.Quantum.Canon;
    function H2BondLengths() : Double[] {//結合の長さ
        return [0.2; 0.25; 0.3; 0.35; 0.4; 0.45; 0.5; 0.55; 0.6; 0.65; 0.7; 0.75; 0.8; //以下省略//];
    }　

    function H2Coeff(idxBondLength : Int) : Double[]　//結合の長さと対応するハミルトンの各項のパラメータ
    {
        let nBondLengths = 54;

        mutable bondCoefficients = new Double[][nBondLengths];

        set bondCoefficients[0] = [0.5678; -1.4508; 0.6799; 0.0791; 0.0791];
        set bondCoefficients[1] = [0.5449; -1.287; 0.6719; 0.0798; 0.0798];
　　　　//（省略）//
        set bondCoefficients[51] = [0.1011; 0.0649; 0.3379; 0.1458; 0.1458];
        set bondCoefficients[52] = [0.0997; 0.0665; 0.3354; 0.1467; 0.1467];
        set bondCoefficients[53] = [0.0984; 0.0679; 0.3329; 0.1475; 0.1475];

        return bondCoefficients[idxBondLength];

    }
    function H2IdentityCoeff(idxBond : Int) : Double　//結合の長さと対応するハミルトンの最初の項のパラメータ
    {
        let coeffIdentity = [2.8489;2.1868;1.7252;1.3827;1.1182;0.9083;0.7381;0.5979;0.4808;//以下省略//];
        return coeffIdentity[idxBond];
    }

    // インデックスが与えられると、水素分子のハミルトニアンに対応する項を返す
    function H2Terms(idxHamiltonian : Int) : (Int[], Int[])
    {
        //This is how a user might input the raw data
        let hamiltonianTerms = [([3], [0]);  ([3],[1]); ([3;3],[0;1]); ([2;2],[0;1]); ([1;1],[0;1])];
        return hamiltonianTerms[idxHamiltonian];
    }

    //結合長さのインデックス、対応するハミルトニアンの項のインデックス、およびステップサイズが与えられると、
    //与えられた項を量子ビットに適用。
    operation H2TrotterUnitariesImpl(idxBondLength : Int, idxHamiltonian: Int, stepSize : Double, qubits : Qubit[]) : ()
    {
        body {
            let (idxPauliString, idxQubits) = H2Terms(idxHamiltonian);
            let coeff = (H2Coeff(idxBondLength))[idxHamiltonian];
            (RestrictToSubregisterCA(
                Exp(IntsToPaulis(idxPauliString), stepSize * coeff, _),
                idxQubits
            ))(qubits);
        }
        adjoint auto
        controlled auto
        controlled adjoint auto
    }

    //結合長のインデックスが与えられると、対応するハミルトニアンの分解を表す演算をユニタリゲートに返す
    function H2TrotterUnitaries(idxBondLength : Int) : (Int, ((Int, Double, Qubit[]) => () : Adjoint, Controlled))
    {
        let nTerms = 5;
        return (nTerms, H2TrotterUnitariesImpl(idxBondLength, _, _, _));
    }

    /// DecomposeIntoTimeStepsフロー制御ライブラリを使用して、上記の分解を表現
    function H2TrotterStepManual(idxBondLength : Int, trotterOrder: Int, trotterStepSize: Double): (Qubit[] => (): Adjoint, Controlled)
    {
        let op = H2TrotterUnitaries(idxBondLength);
        return (DecomposeIntoTimeStepsCA(op, trotterOrder))(trotterStepSize, _);
    }

    //ここでは、Canonを使用してこのプロセスを自動化し、疎なPauli表現を適切な分解に変換する方法を示す

    //CanonのGeneratorTerm型を使用して、特定の結合長のH2ハミルトニアンの項を表現
    function H2GeneratorIndex(idxBondLength : Int, idxHamiltonian : Int) : GeneratorIndex
    {
        let (idxPauliString, idxQubits) = H2Terms(idxHamiltonian);
        let coefficient = (H2Coeff(idxBondLength))[idxHamiltonian];
        return GeneratorIndex((idxPauliString, [coefficient]), idxQubits);
    }

    //CanonのGeneratorSystem型を使用して、与えられた結合長に対応するすべてのハミルトニアン項の和を表現
    function H2GeneratorSystem(idxBondLength : Int) : GeneratorSystem 
    {
        let nTerms = 5;
        return GeneratorSystem(nTerms, H2GeneratorIndex(idxBondLength, _));
    }

    function H2EvolutionGenerator(idxBondLength : Int) : EvolutionGenerator
    {
        return EvolutionGenerator(PauliEvolutionSet(), H2GeneratorSystem(idxBondLength));
    }

    //ここでは、ハミルトンのシミュレーション関数に上記の表現を与えて
    //ハミルトニアンを自動的に適切な演算に分解し、所望の量子ビットに適用できるようにする
    operation H2TrotterStep(idxBondLength : Int, trotterOrder: Int, trotterStepSize: Double, qubits: Qubit[]): () {
        body {
            let simulationAlgorithm = TrotterSimulationAlgorithm(trotterStepSize, trotterOrder);
            simulationAlgorithm(trotterStepSize, H2EvolutionGenerator(idxBondLength), qubits);
        }
        adjoint auto
        controlled auto
        controlled adjoint auto
    }

    //|00〉の初期状態を仮定して、H2基底状態への近似を準備
    operation H2StatePrep(q : Qubit[]) : ()
    {
        body {
            X(q[0]);
        }
    }

    //上記のシミュレーションを使用して、Canonの位相推定アルゴリズムを使用して基底状態エネルギーを知ることができるようになる
    operation H2EstimateEnergy(
            idxBondLength: Int, trotterStepSize: Double,
            phaseEstAlgorithm : ((DiscreteOracle, Qubit[]) => Double)
        ) : Double
    {
        body {
            let nQubits = 2;
            let trotterOrder = 1;
            let trotterStep = H2TrotterStep(idxBondLength, trotterOrder, trotterStepSize, _);

            let estPhase = EstimateEnergy(
                nQubits,
                H2StatePrep,
                trotterStep,
                phaseEstAlgorithm);

            return estPhase / trotterStepSize + H2IdentityCoeff(idxBondLength);
        }
    }

    operation H2EstimateEnergyRPE(idxBondLength: Int, nBitsPrecision : Int, trotterStepSize: Double) : Double
    {
        body {
            return H2EstimateEnergy(
                idxBondLength,
                trotterStepSize,
                RobustPhaseEstimation(nBitsPrecision, _, _)
            );
        }
    }

}

#結果
下記の画像のように、結合の長さに対してエネルギー固有値が表示されたら、成功です。

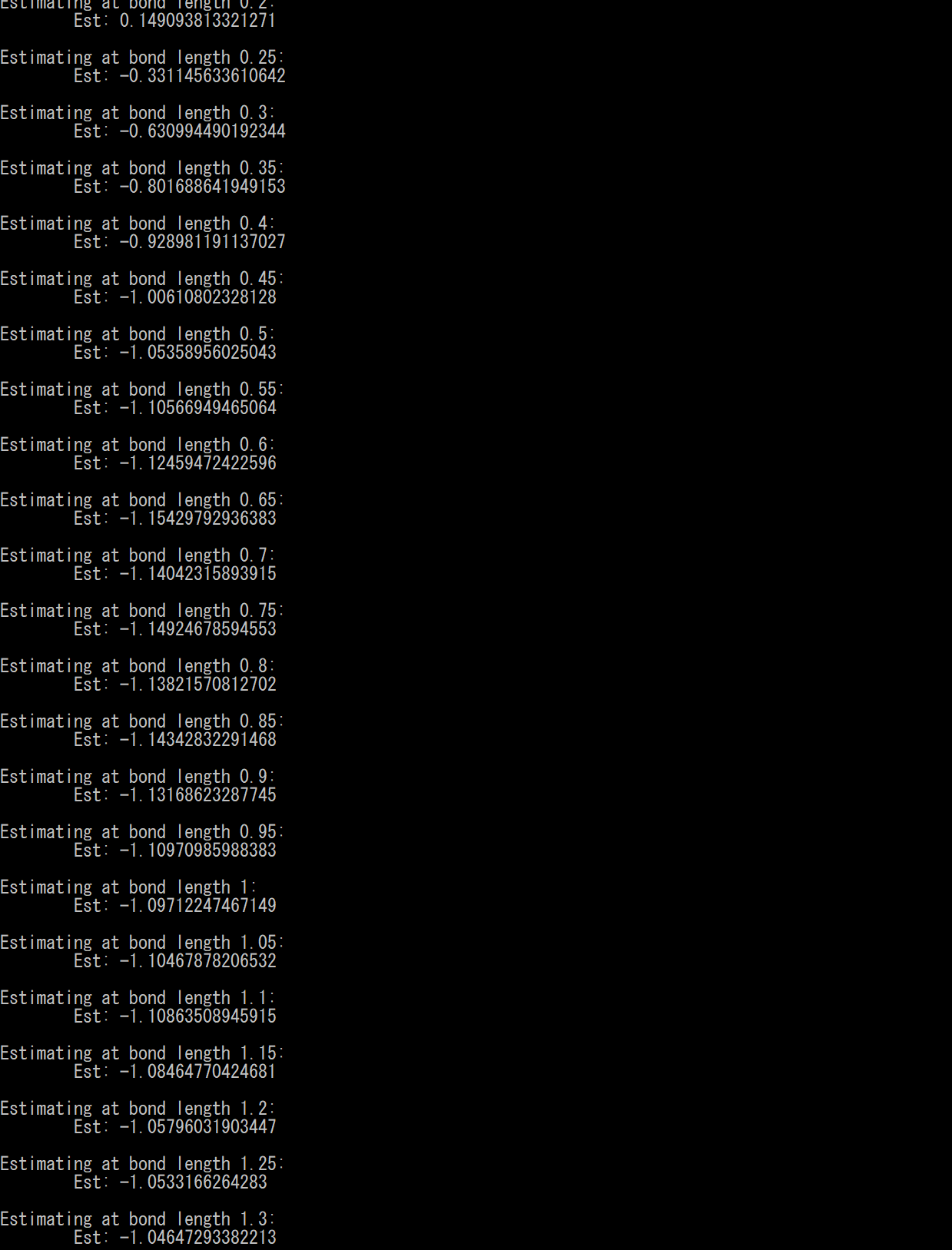
もちろん量子コンピュータを使わず、クライアント上（.net framework上）でシミュレーションしているので、答えはこの論文の通りなのですが、水素原子の状態を２つ量子ビットに準備し、量子回路に各ハルミトニアンの項を配置して固有値を求めています。
上記のサンプルは、重ね合わせ状態ではなくシンプルに位相 $\theta=0$ で各水素原子は |0> の初期状態から計算しています。

#まとめ
（最後時間がなく乱暴な終わらせ方となってしまいましたが）以上のように、マイクロソフトの量子シミュレータは、量子アルゴリズムだけでなく、量子化学のサンプルもあるので、いろいろ試してみると興味深い結果が得られるかもしれません。