はじめに
Type Token Ratio とはある文書における語彙の豊富さを示す指標で
TTR = \frac{V}{N}
(V:異なり語数, N:総語数)
という単純な式で表されます。
テキストマイニングで有名な同志社大の金先生のサイトにも紹介され、たまに論文でも見かける指標ですが、注意して扱わないと間違った結論を引き出しかねません。
というのもTTRにはサンプルサイズ依存性があり、Nが異なる文書間ではTTRを比較することができないからです(したがって上記サイトで安倍首相は福田総理よりも語彙が豊富と結論しているのは誤りだと思う)。以下、説明とその対策を見ていきたいと思います。
サンプルサイズ依存性
この問題はBaayen(2001)の"Word Frequency Distributions"に詳しく書かれています。
一言で言うと、問題は異なり語数Vが総語数Nの増加に対して線形には増加していかないことにあります。TTRは異なり語数を総語数で割ったものなのですが、この性質から、一般的には総語数が少ない文書のほうが高いTTRになりやすいことがわかります。詳しい計算は省きますが、確率的言語モデルの基礎であるUrn modelを仮定すると、異なり語数Vの増加率と総単語数Nの間に
\frac{d}{dN}E[V(N)]=\frac{E[V(1,N)]}{N}
という関係が導かれます。
ここでV(1,N)は頻度スペクトルの記号で、サイズNのコーパスで1回現れる単語の種類の数を表します。
Nが1増えた時に常にV(1,N)が1増えるのであればE[V(N)]の傾きは一定でありVはNに対して線形に増加しますが、これは文章を書いていくときに常に前に使った単語を使わないことを意味するので現実には起こりません。実際には文章の長さが長くなるほど前に使った単語と同じ単語を使う確率が高くなるわけで、Nが十分に大きいときには分子はまれにしか増加しないため、E[V(N)]の曲線は対数関数のようになります。これはUrn modelをシミュレーションすれば容易に確かめることができます。
library(ggplot2)
library(tibble)
# 1000語の珠が入った壺から1つを取り出すことをN回繰り返して、取り出した珠の種類を数えます
urn = function(N){
tokens = floor(runif(N, min=0, max=1000))
types = unique(tokens)
length(types)
}
# Nの長さを1から5001まで100ずつ変えてシミュレーション
tb = tibble(N = seq(1, 5001, 100))
tb = tb %>% rowwise() %>% mutate(V = urn(N))
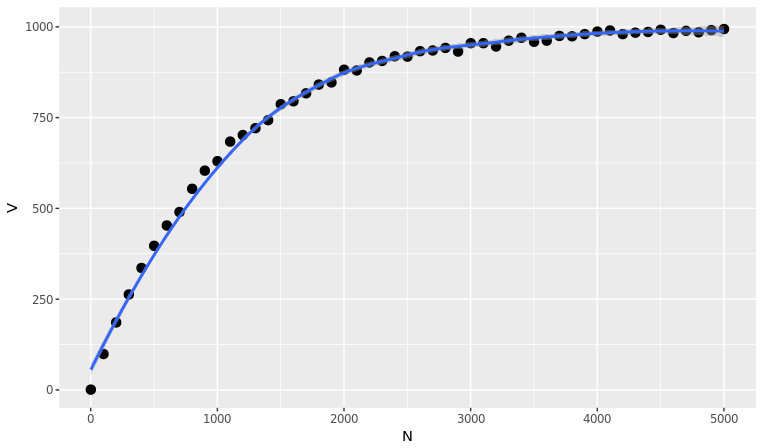
ggplot(tb, aes(N,V)) + geom_point(size = 3) + geom_smooth()
Vの増加がNが大きくなるにつれて鈍化しているのが確認できます。
対策
TTRを使うのをやめてNに依存しないとされるYule's KやZipfのZを使うという手もありますが、おそらく一番有効なのは補正されたTTRを使うことでしょう。つまり「もしNが1000だったらTTRがどのくらいになるか」が分かれば、比べたい文書のTTRをN=1000のときで揃えて比較することができるわけです。
元のコーパスのサイズを$N_0$、修正したいTTRのサイズを$N$とするとTTRの補間/補外は以下の式で与えられます。
V_{N_0}(N)=V({N_0})-\sum_{m=1}^{N_0}(-1)^m(\frac{N}{N_0}-1)^m V(m,N_0)
導出の詳しい経緯などはBaayen(2001)を参照下さい。
実際にこれをPythonコードに書きなおしたものが以下になります。
def interpolation(V0, N0, spectrum, N):
offset = 0
for m in spectrum.keys():
if m%2 == 0:
offset -= ((N/N0 -1)**m) * spectrum[m]
else:
offset += ((N/N0 -1)**m) * spectrum[m]
VN = V0 + offset
return VN
実際の計算は以下のように行いました。
まず、以下のようなデータフレームを用意します.
| Index | 単語 | 単語の数 |
|---|---|---|
| 0 | "新聞 朝 事件 犯罪 …" | 123 |
| 1 | "料理 健康 卵 …" | 98 |
| 2 | "統計 データ データ" | 160 |
| … | … | … |
これをもとに以下のようなコードを実行します
def term2spectrum(terms):
counter = Counter(terms)
m = set(counter.values())
countdict = dict(zip(m, [0]*len(m)))
for w, f in counter.most_common():
countdict[f] += 1
return countdict
def calc_vn(terms, N):
terms = terms.split()
N0 = len(terms)
spectrum = term2spectrum(terms)
V0 = len(set(terms))
VN = interpolation(V0, N0, spectrum, N)
return VN
d = data.sample()
print(d.単語の数)
VNs = []
VN0s = []
for n in range(80, 270):
terms = d.単語.values[0]
VN = calc_vn(terms, n)
VN0 = calc_vn0(terms, n)
VNs.append(VN)
VN0s.append(VN0)
df = pd.DataFrame({"observe":VN0s, "estimated":VNs}, index=range(80, 270))
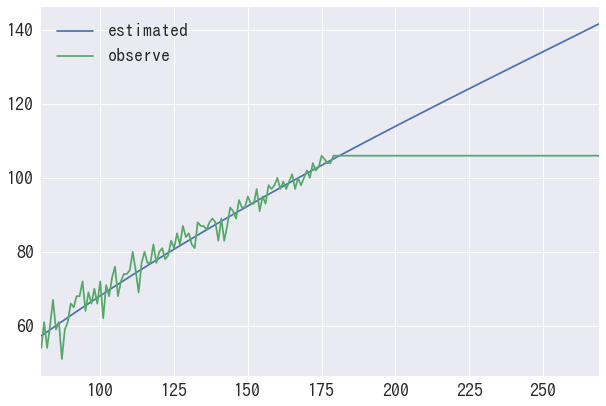
df.plot()
しっかりと補間・補外できています。
タイトルが若干仰々しくなってますが,TTRを使う際にはきちんとこのようにNを調整してやるのが良いという話でした。