はじめに
これは、advent calendar 2019 言語実装 第一日目の記事である。
対象読者は、関数型言語初学者を意識している。
既知の事実のみかつ初歩的なものである。
Shell 、OCaml の基本的な動作は仮定する。
パソコンが Windows のプログラミング初学者であれば、
- オペレーティングシステムとして
Ubuntuをダウンロードし、 - OCaml 言語パッケージマネージャの
opamをインストールする
ことを勧める。
TaPL の紹介
関数型言語に興味がある読者諸君において、" Types and Programming Languages " の名を知らない人はいないであろう。
構成はざっくりといって以下となる。
- 2章 : 型理論の解説 (数学科で教える集合論の上位互換)
- 5章 : ラムダ計算とチャーチ数
- 9章 : 簡単な型ありラムダ計算
- 11-13章 : プログラミングに必要な所々の理論の導入
- 15章 : 部分型
- 20章 : 再帰型
- 24章 : 量化子
今回は2-9章の内容と簡単なコンパイラの実装を駆け足で説明する。
型つきラムダ計算の実装には、23 章の constraint までを入れると、
型推論が可能になるので、かなり実用的なところまでくるが、
そこまでは、advent calendar 一回分では手に追えない。
型理論
TaPL の二章では、「型理論」の導入に入るが、
集合論の醜さと、型理論の心について簡単に触れておこう。
集合論の欠陥
ラッセルのパラドクスというのを聞いたことがあるだろう。
次のような集合を考えよう。
$$ R := \{ x; x \notin x \} $$
$ R $ 自身は、$ R $ に含まれるか、と言う問題が矛盾を生む。
- もし $ R \in R $ ならば、
$ R $ の定義より、$ R $ は、$ R \notin R $ を満たさなければいけない。しかしこれは矛盾 - もし $ R \notin R $ ならば、これは、$ R $ の定義より、$ R $ に属する。つまり、$ R \in R $ となりこれも矛盾
となり、$ R $ 自身は、パラドクスを抱えた存在となる。
パラドクスの解決策
では、どうすればいいか。
ひとつは、集合論の公理を変える方法である、今、すべての要素は、集合 $ R $ に対して、属すか属さないかのどちらかはっきりしなければいけない。といった暗黙の了解があった。これが古典的な集合論の問題であった。
集合論の沼
これに対して、集合論の立場からは、選択公理を仮定してはどうか、排中律を除去してはどうか、など様々な試みが行われたが、最近では理論が悪い意味で肥大化し、やれ強制法はどうだ、など
『「自然数の集合」に対して、「自然数」の演算をあてはめており』、
甚だ見苦しい状況がみられ『センスの無さ』がはっきりと目立つ。
集合論の代替物
現在の数学の大部分は、集合論に否応なしに依存しているが、
グロタンディークらによって整備されたトポス理論(述語をもつ集合のようなもの)などによって、数学のモデルの再開発が現代盛んに行われている。
それらの一つが、Homotopy Type Theory であったり、Topos 理論だったりする。
「集合論の議論を他の理論で書き換える」作業がこれから大切になると見ている。
Kashihara Masaki 氏の Categories and Sheaves では、グロタンディーク宇宙と自然数と少々の規則を仮定して圏論を構成しており、集合論を仮定していない。
あるいは、Homotopy Type Theory などにならい、依存型理論を導入し、Univalence Axiom と Higher Inductive Type の上で、sheaf の定義などをすれば、すっきりとした世界が見えてくることは少し真面目に勉強すればわかることであろう。
集合論は歴史へ移すべき闇(低級理論)の一つと思う。
型理論の提唱
実は、ラッセルは、パラドクスの提唱とともに、シンプルな解決策(型理論)を示している。
それは一言で言えば、「各々の集合に対する『述語』の導入」である。述語とは、「一項関係 p (集合の一つの要素を引数にとり、ブール値 True を返す関数)」である。
「型」とは「述語をもつ集合」のことである。
さきほどのパラドクスを例として見てみよう。
$ p(x) $ は、$ x $ がその集合の要素であれば $ true $ 、要素でなければ $ false $ を返すものとする。
$$ R := \{ x; x \notin x \land p(x) \} $$
こうすると、さきほどのパラドクスはどうなるかというと、
- もし、$ R \in R $ ならば、 $ p(x) = true $ 、$ R \notin R $ となり、矛盾。
- もし、$ R \notin R $ ならば、$ p(x) = false $ 、この時点で、$ R $ は、無事集合に含まれる条件を満たさない。
以上により、2 が真となり、$ R $ は自身に属さない。
すなわち、ラッセルのパラドクスは回避された。
ラッセル自身によって示されたこの方法は極めてシンプルかつ美しいものであった。
しかしながら、ラッセルがパラドクスを提唱した当時の型理論では、
非常に困難な事象が多々見受けられたようだ、細かい仕様において、
集合論では扱えるところをでは、型理論ではどのように扱うのかなどといった話である。
代表的なものは、再帰的定義についてであったと記憶している。
型理論の発展
近年、Homotopy Type Theory がよくよく話題に上がってきている。
ラムダ計算と命題論理の curry howard 対応に、homotopy の理論を融合したものである。
Martin Lof の提唱した、依存型理論に対して、
univalence axiom と Higher Inductive Types を導入し、数学の基盤の再構築を行っている。
より詳しく言えば、単体の圏の関手圏上に展開される groupoid の言葉で記述される ∞-category の理論である。理解には、kan 拡張に精通している必要があるので、ここでは触れない。
詳しくは下記を参考にされたい。
kan 拡張の理解には、
- [Kashiwara, Schapira] categories and sheaves
を強く薦める。
圏論の骨格をなす極限とこの理論を、よくまとめたものは現時点ではこれ以外に見たことがない。
2章 型理論の基礎
TaPL の2章で覚えておく定義は
- $ \mathcal{P} \ ( \mathcal{S} ) := S $ の
冪集合 - $ \mathcal{S} \ \backslash \ \mathcal{T} := \text{集合} \ S \ \text{と集合} \ T \ $ の
差 - $ \mathbb{N}\ \ \ \ \ \ \ := $
自然数の集合 - $ P(s) := s \in P \ \ \ \ \ $ :
Predicate ( 1-place relation ) - $ s R t := ( s , t ) \in R $ :
Binary Relationwhere $ s, t \in \mathcal{ U } $ - $ s R t := ( s , t ) \in R $ :
2-placed Relationwhere $ s \in \mathcal{S} , t \in \mathcal{T} $ - $ \Gamma \vdash s : T \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $ :
3-placed Relation( Typing Relation (see Chapter 9) ) - $ R $ is
n-placed relation$ \iff $- $ s_1 \in \mathcal{S_1} , ... , s_n \in \mathcal{S_n} $ are
relatedif $ (s_1, ... , s_2) \in R $
where $ R \subseteq \mathcal{S_1} \times ... \times \mathcal{S_n} $
- $ s_1 \in \mathcal{S_1} , ... , s_n \in \mathcal{S_n} $ are
- $ R $ is
Partial Function$ \iff $ $ s R t_1 \wedge s R t_2 \Rightarrow t_1 = t_2 $ - $ R $ is
Total Function$ \iff $ $ dom(R) = \mathcal{S} $ where $ \mathcal{S} R \mathcal{T} $ - Partial Function $ s R t $ is defined on $ s \in \mathcal{S} $ if $ s \in dom(R) $
- $ f(x) \uparrow $ , $ f(x) = \uparrow $ : $ f $ is undefined on $ x $
- $ f(x) \downarrow $ , $ f(x) = \downarrow $ : $ f $ is defined on $ x $
-
Diverge/Failure- function の実装時、出力値
failureは 出力値divergenceと区別しないといけない. - fail を出力する関数は Partial であり divergeble であり得るが、Total であれば、入力に再帰は含まれない
- Rの input である$ dom(R) $ は、$ \mathcal{S} $ の要素に限られる
- function の実装時、出力値
つぎにラムダ計算の基本に入ろう。
5章(前半) 型なしラムダ計算 と チャーチ数
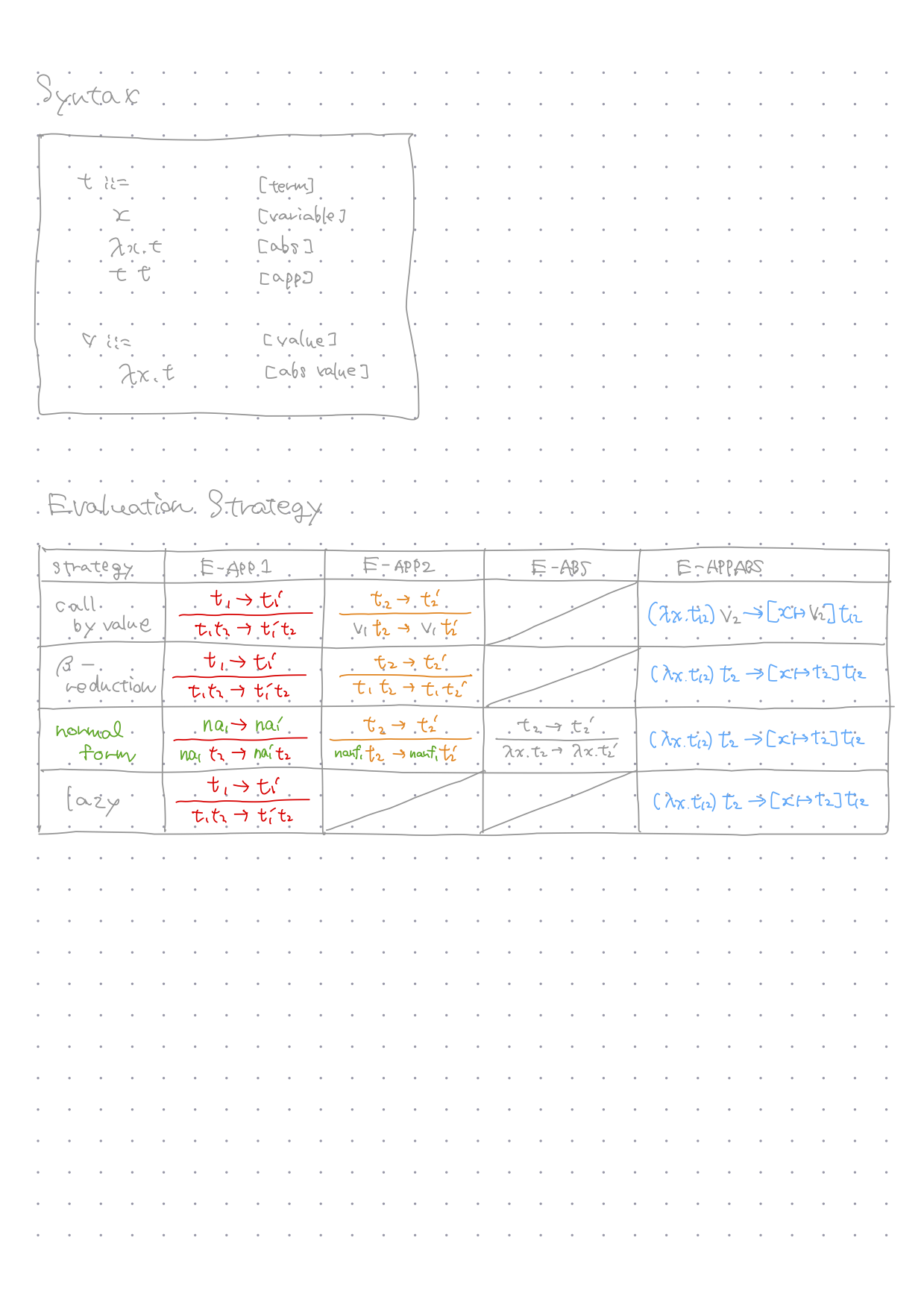
ラムダ計算の構文は、
t := x <variable>
| λx. t <λ abstraction>
∣ t t <application>
と定義される。これは、「term t は、
- 変数である
- λ式(関数)である。
- 関数適用である
の三つの必ずどれかにあたる。」と言う意味である。
ラムダ計算の「評価規則」は、
(λx. t) t' → t[x↦t']
で与えられ、右側は、「t の中に現れるx をすべてt' で置換する」という意味である。
以上の定義に従うと、
ラムダ抽象<λ abstraction> とは、例えば以下のような S, K があげられる。
K := λx. λy. x
S := λx. λy. λz. ((x)(z))(y z)
Kは、x と y とを引数にとり、 x を返す関数である。
Sは、x と y と z を引数にとり、(x z)(y z) を返す関数である。
S K K x
= ((K)(x))(K x)
= (λx. λy. x) (x) (K x)
= x
となり、恒等関数 I := S K K が定義されたが、この計算において、
関数適用がどういうものか、直感的に理解していただければ幸いである。
church booleans
このような簡単な機械的な操作から数字を定義することができる。
それがチャーチ数の概念であるが、
その前に、チャーチブーリアンを定義しておこう。
tru := λt.λf. t
fls := λt.λf. f
and := λx.λy. x y fls
or := λx.λy. y tru x
not := λx. x fls tru
pairs
pair := λf.λs.λb. b f s
fst := λp. p tru
snd := λp. p fls
if
以上のようにチャーチブーリアンを定めると、if 式は、条件と項をならべるだけで定義できてしまう。
if b s t = b s t
church numerals
チャーチ数の定義に入ろう。
チャーチによる、自然数 $ \mathbb{N} $ は以下のように定義される
0 := λs.λz. z -- = λx.λy. y = fls
1 := λs.λz. s z
2 := λs.λz. s (s z)
3 := λs.λz. s (s (s z))
...
これは、次のように書くこともできる。
0 x y := y
1 x y := xy
2 x y := x(xy)
3 x y := x(x(xy))
...
succ
チャーチ数の定義にでてくる、
s は successor を、z はzero をあらわしているが、では、
successor をこのチャーチ数に対して定めてみよう。
S0xy = xy
S1xy = x(xy)
S2xy = x(x(xy))
...
であることから、s を逆算してみると、
x(x(xy)) = x(2xy) = S2xy
x(xy) = x(1xy) = S1xy
so, Snxy = x(nxy)
or
x(x(xy)) = 2x(xy) = S2xy
x(xy) = 1x(xy) = S1xy
so , Snxy = nx(xy)
の二通りの定め方が少なくとも可能である。
suc = λn.λs.λz. s(nsz)
= λn.λs.λz. ns(sz)
plus
加算は次のように定義する。( x, y はsucc と zero )
plus := λm.λn.λx.λy. mx(nxy)
plus m n x y = mx(nxy)
plus m n x y
= x(x(x(x(xy))))
= mx(nxy)
times
乗算は次のように考えることができる。
times m n x y
= x(x(x(x(x...(xy))))) // x appears m * n
= x(x(x( ))) // now m = 3
= mx (x(x...(xy)))
= mx(mx(mx..(mxy))) // mx appears by n times
= n(mx)y
or similarly
= m(nx)y
よって、まとめると、
times := λm.λn.λx.λy. m(nx)y
times := λm.λn.λx.λy. n(mx)y
また、先ほどの加算を使用すると次のように定義することもできる。
times = λm.λn. m(plus n)0
times m n = m(plus n)0
pow
同様に、
pow = λm.λn. m(times n)1
pow m n = m(times n)1
別の方法として、
pow = λm.λn. n m
pow m n = n m
iszro
iszro := λm. m (λx.fls) tru
iszro m := let F x = fls in
m F tru
例
iszro 5
= 5 F tru
= F(F(F(F(F tru))))
= fls // because F always returns fls
iszro 0
= 0 F tru
= tru
prd
predicator とは、successor の逆で、直前の数を返す関数である。
ただし、0 に対しては、0 を返す。
prd の実装はいままでとは異なり、少し難しい。
zz := pair 0 0
ss p := pair (snd p) (+ 1 (snd p))
とふたつの関数を用意したうえで、
prd は次のように定義される。
prd m = fst (m ss zz)
例を見てみよう。
prd m
= fst (m ss zz)
= fst (ss(ss(...(ss zz)...)))
= fst (pair {m-1} m)
= m-1
where,
ss zz
= pair (snd (pair 0 0)) (+ 1 (snd (pair 0 0)))
= pair 0 1
ss (ss zz)
= pair (snd (pair 0 1)) (+ 1 (snd (pair 0 1)))
= pair 1 2
...
以上のようにして、直前の数字を正しく返す仕組みを持っていることがしっかりと見て取れるであろう。
prd 0
= fst (0 ss zz)
= fst (zz)
= fst (pair 0 0)
= 0
sub
引き算は、prd をつかって定義され、
sub m n := n prd m
equal / or and
equal m n := and (iszro (sub m n))(iszro (sub n m))
ここで、論理演算士の定義は以下のようであったことを思い出そう。
or := λb.λc. b tru c
and := λb.λc. b c fls
list
TaPL において、紹介されている List の定義はとてもおもしろい。
c は、cons オペレータ、n はnull を表している。
succ zero と同じ仕組みであることに注意されたい。
(ともに、始代数という代数構造が入っており、非常に理論として汎用性があり、綺麗なものである。)
[x,y,z] c n := cx(cy(czn))
[x,y] c n := cx(cyn)
[x] c n := cxn
nil c n := n
と定めればよいが、ここまでで、
nil == fls == zero とこれら三つの関数がλ式としては、同一のものであることに注意されたい。
cons オペレータの定義は以下となる。
cons x list c n := c x (list c n)
この定義により、以下の二式が導出される。
cons x [y,z,a,...] == [x,y,z,a,...]
cons x nil == [x]
よって、list は cons を用いて、次のように書くことができる。
[x,y,z,a,b]
== cons x [y,z,a,b]
== cons x (cons y [z,a,b])
== cons x (cons y (cons z [a,b]))
== cons x (cons y (cons z (cons a [b])))
== cons x (cons y (cons z (cons a (cons b nil))))
例
cons x [y,z] c n
= c x ([y,z] c n)
= c x (c y (c z n))
isnil は、次のように定義される。
isnil list := list F tru
where F x y := fls
例
isnil nil
= nil F tru
= tru
isnil [x,y]
= [x,y] F tru
= F x (F y tru)
= fls
head 関数は、
head list = list tru nil
tail 関数は、prd の時と同様に考えて、
pair nil nil
pair nil [z]
pair [y] [y,z]
pair [y,z] [x,y,z]
...
tail list = fst (list cc nn)
cc x p = pair (snd p)(cons x (snd p))
nn = pair nil nil
tail [x,y,..,z]
= fst ([x,y,..,z] cc nn)
= fst (cc x (cc y(..(cc z nn)..)))
= fst (cc x (cc y(..(pair nil [z])..)))
= fst (pair [y,..,z] [x,y,..,z])
= [y,..,z]
リストの実装方法として、別の方法があり、
nil = pair tru tru;
cons = λh. λt. pair fls (pair h t);
head = λz. fst (snd z);
tail = λz. snd (snd z);
isnil = fst;
のように定義することができるが、
[x,t,..,z] c n = cx(cy(..(czn)))
のような始代数の構造は持たない。
Enriching Calculus
Recursion
再帰計算の肝となるのが、不動点コンビネータ(関数)である。
fixed point λ function
fix = λf. (λx.f ( λy.xxy )) (λx.f ( λy.xxy ))
f_sumlist = λrec.λl. test (isnil l)
(λx. 0)
(λx. plus (head l) (rec (tail l)))
sumlist = fix f_sumlist
ただし、sumlist 関数は、
不動点コンビネータを使わずとも、
先ほどのリストの定義の代数構造を利用して、次のようにもかける。
sumlist := λx.x plus 0
e.g.
sumlist [x,y,z]
= [x,y,z] plus 0
= plus x ( plus y ( plus z 0 ))
さらに
prodlist := λx.x times 1
e.g.
prodlist [x,y,z]
= [x,y,z] times 1
= times x ( times y ( times z 1 ))
foldr := λx. λf. λi. x f i
e.g.
foldr [x,y,z] f i
= [x,y,z] f i
= f x ( f y ( f z i ))
といった、畳み込み関数なども上のように、代数構造を利用すれば再帰なしに定義できる。
型つきラムダ計算へ
このように、
ラムダ計算を定義してしまえば、かなりのことが可能になる。
実際、ラムダ計算はチューリング完全であり、実際、任意のプログラムをλ式で書くことが可能である。
型の無いラムダ計算では、完全に自由なことができる。
ラムダ計算は、関数の羅列であり、
それぞれの関数には、入力domain と 出力codomain がとてもはっきりしている。
そこで、λ式を
- domain に型をあてがうことで、入力を制限し、
- codomain に型をあてがうことで、出力を制限する。
これをすべての項に対して、適用することができるのが、型つきラムダ計算である。
型エラーにより、検出できるバグはすべて排除することができるようになる。
(番外編) Yacc
Yacc は、(構文からプログラミング言語を自動生成くれる)Parser コンパイラである。
抽象構文を書けば、後は、自動でやってくれる優れものである。
Yacc は通常 C言語で書かれたものが、古くからあるが、
OCaml で書かれた OCamlYacc/OCamlLex は OCaml に元から備わっている。
例えば、足し算だけからなる項の抽象構文は次のようなものである。
term := num
| term + term
こうした抽象構文を解析するのが、構文解析器 Parser の役割である。
TaPL を読んだところで、コンパイラに関するちょっとした知識がなければ
言語実装ができないので、簡単な足し算電卓の実装の例で
OCaml Yacc と OCamlLex の使い方を見ていくことにしよう。
以下のコードは電卓の全コードであり、
calc0.mly lexer.mll Makefile main.ml を各ファイルごとに保存し、
make を実行すれば「足し算のみの電卓」ができあがる。
###########################
#### calc0.mly ####
###########################
%{
open Printf
%}
%token <float> NUM
%token PLUS
%token NEWLINE
%left PLUS
%start input
%type <unit> input
%%
input: { }
| input line { }
;
line: NEWLINE { }
| expr NEWLINE { printf "\t%.10g\n" $1; flush stdout }
;
expr: NUM { $1 }
| expr PLUS expr { $1 +. $3 }
;
%%
###########################
#### lexer.mll ####
###########################
{
open Calc0
}
let digit = ['0'-'9']
rule token = parse
| [' ' '\t'] { token lexbuf }
| '\n' { NEWLINE }
| digit+ (* '+' ∈ RegExp *)
| "." digit+
| digit+ "." digit* as num { NUM (float_of_string num) }
| '+' { PLUS }
| _ { token lexbuf }
| eof { raise End_of_file }
#########################
#### main.ml ####
#########################
let parse_error s = print_endline s; flush stdout
let main () =
try
let lexbuf = Lexing.from_channel stdin in
while true do
Calc0.input Lexer.token lexbuf
done
with
End_of_file -> exit 0
| Parsing.Parse_error -> parse_error "Parse error"
let _ = Printexc.print main ()
##########################
#### Makefile ####
##########################
all:
ocamlyacc *.mly
ocamlc -c *.mli
ocamllex lexer.mll
ocamlc -c *.ml
ocamlc -o calc *.cmo
clean:
rm -rf *.mli *.cmo *.cmi calc lexer.ml calc0.ml
lexer
lexer は、入力に対して、パターンマッチを施し、パターンにマッチすれば、{}内のterm をあてがえる機械である。
パターンマッチには、正規表現を使用しており、例えば、digit+ は、digit の一回以上繰り返しという意味である。
digit はここでは、0 から9 までの char と定めている。
let digit = ['0'-'9']
rule token = parse
| digit+ (* '+' ∈ RegExp *)
| "." digit+
| digit+ "." digit* as num { NUM (float_of_string num) }
| '+' { PLUS }
| _ { token lexbuf }
| eof { raise End_of_file }
parser
parser に関しては、先に述べたとおりで、抽象構文を書いておけばよい。
右側の{}の中には、構文解釈時に実行される、OCaml のコードが入る。
例えば、一番下の例では、最初の expr で返り値と、三番目の expr の返り値の浮動小数点の和を返す。と言う意味である。
input: { }
| input line { }
;
line: NEWLINE { }
| expr NEWLINE { printf "\t%.10g\n" $1; flush stdout }
;
expr: NUM { $1 }
| expr PLUS expr { $1 +. $3 }
;
5章(後半) 評価戦略
関数型言語あるいは、ラムダ計算の言語実装には、
大きく分けて二つの評価戦略がある。
さきほどはざっくりと評価戦略は
(λx. t) t' → t[x↦t']
だと言ったが、これでは、t と t' のどちらから先に計算すればよいのかなど不確定な情報が多く、それらは実装に依存する。
これを避けるために、明示的に評価戦略を示してやる必要がある。
評価戦略というのは、構文木のどこからどのような規則で、返り値をもとめていくか。
ということである。
電卓の簡単な例でいえば、1+1*1 の掛け算を先にするのか、足し算を先にするのか、といった問題も評価戦略の問題である。
TaPL に記載されている4つの評価戦略は次のとおりである。
実際に、これらの計算を
times (times 3 (times 2 1)) に対して、適用したのが、次である。
call by value
OCaml は、call by value という評価戦略を採用しており、実装は以下のようになる。
let rec isval ctx = function
| TmAbs(_,_,_,_) -> true
| _ -> false
let rec eval1 ctx = function
| TmApp(fi,TmAbs(_,x,tyT11,t12),v2) when isval ctx v2
-> termSubstTop v2 t12
| TmApp(fi,v1,t2) when isval ctx v1 -> TmApp(fi,v1,eval1 ctx t2)
| TmApp(fi,t1,t2) -> TmApp(fi,eval1 ctx t1,t2)
| _ -> raise NoRuleApplies
let rec eval ctx t =
try eval ctx (eval1 ctx t)
with NoRuleApplies -> t
6章 de bruijn 記法
Context Γ の導入
通常のラムダ計算では、変数を使うが、
変数に数字を用いて名前を付け、Γ に保存する。この Γ を Name Context と呼ぶ。
例えば、Γ = { a $\mapsto$ 2, b $ \mapsto $ 1, c $ \mapsto $ 0 } であれば、3つの変数が保存されている。
この Name Context によって
たとえば、(a b) c は、(2 1) 0 と解釈することができる。
λc.λd.c d dのように、「束縛変数」を2個持つ式は、
Γ に新たに2つの mapping を、
Γ = {a $\mapsto$ 4, b $ \mapsto $ 3, c $ \mapsto $ 2, c' $ \mapsto $ 1, d $ \mapsto $ 0} と「右から積む」ことで、
λ.λ.1 0 0のように表記することができる。
SHIFT / SUBSTITUTION
このように、新しい変数を積む際に、自由変数 {a,b,c} に関しては、 +2だけ shift してやる必要がある。そして、一時限りの束縛変数を使用したあとは、逆に-2 shift してやる必要がある。
これが具体的に行われるのは、 Application (λx.t) s の次の工程、
Substitution [x ↦ s] t においてである。
これを実装したものが、
shift / substitution
である。。
(* syntax.ml *)
...
(* -------------------------------------------------- *)
(* Shifting *)
let rec walk funOnVar c = let f = funOnVar in function
| TmVar(fi,x,n) -> funOnVar fi c x n
| TmAbs(fi,x,tyT,t2) -> TmAbs(fi,x,tyT,walk f(c+1)t2)
| TmApp(fi,t1,t2) -> TmApp(fi, walk f c t1, walk f c t2)
| TmIf(fi,t1,t2,t3) -> TmIf(fi,walk f c t1, walk f c t2, walk f c t3)
| TmSucc(fi,t) -> TmSucc(fi, walk f c t)
| TmPred(fi,t) -> TmPred(fi, walk f c t)
| TmIsZero(fi,t) -> TmIsZero(fi, walk f c t)
| x -> x
let termShiftOnVar d = fun fi c x n -> if x>=c then TmVar(fi,x+d,n+d) else TmVar(fi,x,n+d)
let termShiftAbove d = walk (termShiftOnVar d)
let termShift d = if d>=0 then print_endline ("SHIFT: "^(string_of_int d));termShiftAbove d 0
(* -------------------------------------------------- *)
(* Substitution *)
let termSubstOnVar j s t = fun fi c x n -> if x=j+c then termShift c s else TmVar(fi, x, n)
let termSubst j s t = walk (termSubstOnVar j s t) 0 t
let termSubstTop s t = print_endline "SUBSTITUTE: "; termShift (-1) (termSubst 0 (termShift 1 s) t)
9章 型付きラムダ計算
型付きラムダ計算とは、項t に対し、Type Context $ \Gamma $ と、型 $ T $ を追加したものである。実装において、この Type Context $ \Gamma $ と、さきほど出てきた Name Context $ \Gamma $ など、様々な種類の Context をタグ付けすることにより、同じ型の Context として実装している。(ただし実行時、構文解析器が使用する Name Context と、型検査機が使用する Type Context は異なるインスタンスである。)この Context $ \Gamma $ は、このように実行時における様々な環境要素を含んでいるため、コンパイラの実行時環境などと呼ぶこともあるが、実行時環境には他にもC(Constraint 22章) や Σ(Store 16章) などがあり、曖昧性をもつ。そのためふつう $ \Gamma $ は、「 (Type) Context 」と呼ぶ。
コンテクストと、項、型の関係は次のような関係 ( 3-placed relation ) で表し、
$ \Gamma \vdash t : T $
「コンテクスト $ \Gamma $ における項 t の型は、T である」とよむ。
構文 Syntax
型付ラムダ計算の最も小さい構文は、
t ::= term
x variable
λx:T.t abstraction
t t application
v ::= value
λx:T. t abstraction value
T ::= type
T → T arrow type
Γ ::=
∅ empty context
Γ,x:T term variable binding
である。
値 v は、それ以上単独で評価することができない項である。さきほど述べた、評価戦略 call by value の策定に、この v が大きく関わってくる。
型 T は、すべての項は関数だという、関数型言語の思想をよく表しており、すべて Arrow Type の形でかける。実際の実装では、これに$ \mathbb{B} $ のような基本型を加えるので、以下の方が想像しやすいのかもしれない。
T ::= type
B boolean type
T → T arrow type
といった具合である。
Γ は、Type Context である。
評価規則 Evaluation Rules
評価規則は、先ほどのとおりである。
t1 → t1'
-------------------------------------- [E-APP1]
t1 t2 → t1' t2
t2 → t2'
-------------------------------------- [E-APP2]
v1 t2 → v1 t2'
(λx:T11.t) v2 → [x ↦ v2] t [E-APPABS]
型付け規則 Typing Rules
これに、型規則を導入したが形有りラムダ計算である。
x : T ∈ Γ
-------------------------------------- [T-VAR]
Γ ∣- x : T
Γ,(x:S) ∣- t : T
-------------------------------------- [T-ABS]
Γ ∣- λx:S.t : X → T
Γ |- t1 : T2 -> T , Γ ∣- t2 : T2
-------------------------------------- [T-APP]
Γ ∣- t1 t2 : T
実装
具体的実装における構文や、
型規則、評価戦略は以下のようになる。
型規則は、typeof 関数の実装であり、
評価戦略は、eval1 関数の実装である。
ソースコードは、github レポジトリにある。
構文
/* Modules both for Interpreter and for Compiler */
Command : /* A top-level command */
| Term { fun ctx -> let t = $1 ctx in Eval(tmInfo t,t),ctx }
| LCID Binder { fun ctx -> ((Bind($1.i,$1.v,$2 ctx)), addname ctx $1.v) }
Binder :
| COLON Type { fun ctx -> VarBind($2 ctx) }
Type :
| ArrowType { $1 }
AType :
| LPAREN Type RPAREN { $2 }
| BOOL { fun ctx -> TyBool }
| NAT { fun ctx -> TyNat }
ArrowType :
| AType ARROW ArrowType { fun ctx -> TyArr($1 ctx, $3 ctx) }
| AType { $1 }
Term :
| AppTerm { $1 }
| LAMBDA LCID COLON Type DOT Term
{ pe "PARSER: λx:T.t"; fun ctx -> let ctx1=addname ctx $2.v in TmAbs($1,$2.v,$4 ctx,$6 ctx1)}
| IF Term THEN Term ELSE Term { fun ctx -> TmIf($1, $2 ctx, $4 ctx, $6 ctx) }
AppTerm :
| ATerm { $1 }
| SUCC ATerm { fun ctx -> TmSucc($1, $2 ctx ) }
| PRED ATerm { fun ctx -> TmPred($1, $2 ctx ) }
| ISZERO ATerm { fun ctx -> TmIsZero($1, $2 ctx) }
| AppTerm ATerm { fun ctx -> let e1=$1 ctx in TmApp(tmInfo e1,e1,$2 ctx) }
ATerm : /* Atomic terms are ones that never require extra parentheses */
| LPAREN Term RPAREN { pe "PARSER: ( t )"; $2 }
| LCID { fun ctx -> TmVar($1.i, name2index $1.i ctx $1.v, ctxlength ctx) }
| TRUE { fun ctx -> TmTrue($1) }
| FALSE { fun ctx -> TmFalse($1) }
| INTV { fun ctx -> let rec f = function
0 -> TmZero($1.i)
| n -> pe "succ"; TmSucc($1.i, f (n-1))
in f $1.v }
評価器
open Format
open Core
open Support.Pervasive
open Support.Error
open Syntax
open Arg
open Type
exception NoRuleApplies
let rec isnumericval ctx = function
| TmZero(_) -> true
| TmSucc(_,t1) -> isnumericval ctx t1
| _ -> false
let rec isval ctx = function
| TmAbs(_,_,_,_) -> true
| TmTrue(_) -> true
| TmFalse(_) -> true
| t when isnumericval ctx t -> true
| _ -> false
let rec eval1 ctx = function
| TmApp(fi,TmAbs(_,x,tyT11,t12),v2) when isval ctx v2
-> termSubstTop v2 t12
| TmApp(fi,v1,t2) when isval ctx v1 -> TmApp(fi,v1,eval1 ctx t2)
| TmApp(fi,t1,t2) -> TmApp(fi,eval1 ctx t1,t2)
| TmIf(_,TmTrue(_),t2,t3) -> t2
| TmIf(_,TmFalse(_),t2,t3) -> t3
| TmIf(fi,t1,t2,t3) -> let t1' = eval1 ctx t1 in TmIf(fi, t1', t2, t3)
| TmSucc(fi,t1) -> let t1' = eval1 ctx t1 in TmSucc(fi, t1')
| TmPred(_,TmZero(_)) -> TmZero(dummyinfo)
| TmPred(_,TmSucc(_,nv1)) when (isnumericval ctx nv1)
-> nv1
| TmPred(fi,t1) -> TmPred(fi, eval1 ctx t1)
| TmIsZero(_,TmZero(_)) -> TmTrue(dummyinfo)
| TmIsZero(_,TmSucc(_,nv1)) when (isnumericval ctx nv1)
-> TmFalse(dummyinfo)
| TmIsZero(fi,t1) -> let t1' = eval1 ctx t1 in TmIsZero(fi, t1')
| _ -> raise NoRuleApplies
let rec eval ctx t =
try eval ctx (eval1 ctx t)
with NoRuleApplies -> t
let rec process_command ctx = function
| Eval(fi,t) ->
let tyT = typeof ctx t in
printtm_ATerm true ctx (eval ctx t);
print_break 1 2; pr ": "; printty tyT; force_newline(); ctx
| Bind(fi,x,bind) -> pr ("Now, "^x^ " is a variable: "); prbindingty ctx bind; force_newline(); addbinding ctx x bind
let print_eval ctx cmd =
open_hvbox 0;
process_command ctx cmd;
print_flush ()
型解釈器
open Format
open Core
open Support.Pervasive
open Support.Error
open Syntax
open Arg
exception NoRuleApplies
(* ----------- TYPING --------------- *)
let rec typeof ctx t = pr "TYPEOF: ";printtm ctx t;print_newline (); match t with
| TmVar(fi,i,_) -> getTypeFromContext fi ctx i
| TmAbs(fi,x,tyT1,t2) ->
let ctx' = addbinding ctx x (VarBind(tyT1)) in
let tyT2 = typeof ctx' t2 in
TyArr(tyT1,tyT2)
| TmApp(fi,t1,t2) ->
let tyT1 = typeof ctx t1 in
let tyT2 = typeof ctx t2 in
(match tyT1 with
| TyArr(tyT11,tyT12) -> if (=) tyT2 tyT11 then tyT12 else error fi "type mismatch"
| _ -> error fi "arrow type expected" )
| TmTrue(fi) -> TyBool
| TmFalse(fi) -> TyBool
| TmZero(fi) -> TyNat
| TmSucc(fi,t) -> if (=) (typeof ctx t) TyNat then TyNat else error fi "succ expects 𝐍"
| TmPred(fi,t) -> if (=) (typeof ctx t) TyNat then TyNat else error fi "succ expects 𝐍"
| TmIsZero(fi,t) -> if (=) (typeof ctx t) TyNat then TyBool else error fi "iszero expects 𝐍"
| TmIf(fi,t1,t2,t3) -> if (=) (typeof ctx t1) TyBool then
let tyT2 = typeof ctx t2 in
if (=) tyT2 (typeof ctx t3) then tyT2 else error fi "resulting type of if statement mismatch"
else error fi "if-condition expects a boolean"
(* ---- *)
let prbindingty ctx = function
| NameBind -> ()
| VarBind(tyT) -> pr ": "; printty tyT
(番外編) 左再帰と右再帰
構文解析の知識
構文には、左再帰構文と呼ばれる構文と、右再帰構文と呼ばれる構文がある。
正規表現 ab* の構文の定義方法として、
Left Recursion
t ::=
| a
| t b
という定義方法があり、これを左再帰という。
文 abbb を解析すると、
((((a) b) b) b)
t
/ \
t b
/ \
t b
/ \
t b
/
a
これに対し、右再帰構文とは、
Right Recursion
t ::=
| a s
s ::=
| ∅
| b s
のような定義であり、
(a (b (b (b ∅))))
t
/ \
a s
/ \
b s
/ \
b s
/ \
b ∅
というように、右へ、構文木が垂れ下がっていく。
構文解析器、字句解析器ともに、通常文を左から順番に読み込んでいく(走査していく)。
文を左から走査していくとき、
右再帰構文では、最後の∅ が見えるまで、s も t もその内容物が確定しないのに対して、
左再帰構文では、毎度毎度、各 t の内容物が確定する。
コンパイラとインタプリタの違い
インタプリタは止まらなくてもいいので、とりあえず、入力の最初から順番に評価していけばよいが、
入力の列が途絶えるかどうかはまったく気にしなくてよい。むしろ気にしてはいけない。入力が終了するのを待っていては、対話式インタプリタはかけない。
これに対し、コンパイラは、入力が一区切り付いたかどうかなどはどうでもよく、終了したのか終了していないのかは決定しないければいけない。
この意味で、コンパイラとREPLとで採用される構文は、「左再帰」と「右再帰」という相反する構文をそれぞれが目的に応じて採用するのが適当である。
/************ REPL **********************************************/
input : /* Left Recursion */
| { fun _ -> [],[] }
| input DOUBLESEMI { fun ctx -> [],ctx }
| input oneREPL { let _,ev_ctx = $1 [] in
let cmds,_ = $2 ev_ctx in
let ev_ctx' = process_commands ev_ctx cmds in
fun _ -> [],ev_ctx' }
oneREPL :
| Command DOUBLESEMI { fun ctx -> let cmd,ctx' = $1 ctx in [cmd],ctx' }
| Command SEMI oneREPL { fun ctx -> let cmd,ctx' = $1 ctx in
let cmds,ctx'' = $3 ctx' in cmd::cmds,ctx'' }
/************ COMPILER *********************************************/
toplevel : /* Right Recursion */
| EOF { fun ctx -> [],ctx }
| Command SEMI toplevel { fun ctx -> let cmd,ctx = $1 ctx in
let cmds,ctx = $3 ctx in cmd::cmds,ctx }
補足
通常のコンパイラ実装では、
これらの、
- 字句解析器
- 構文解析器
- 型検査型推論器
に加え、
- 最適化
- ガーベッジコレクション
- コード生成
などを実装する必要があるが、
実装言語(C, OCaml) などに元から備わってあるものを利用することで、それらの実装は回避することができる。
おわりに
実装では、型つきラムダ計算のシステムに対して、
BOOLEAN と NATURALNUMBERS を付加してある。
型付きラムダ計算を、型規則とともに、拡張していくことで、
非常に豊かなプログラミング言語が実現できる。
11 章では、let 式、sequence, ascription, record , variant, string, float などを付加し、
15 章では、subtype を付加し、record type の順序問題を解決しつつ、object oriented 言語の風合いを出すことを可能にしている。
20 章以降では、再帰型を導入し、ocaml の letrec 式の型付けや、再帰型代数的データ構造を、現実化している。
23 章以降は、polymorphism を本格的に導入し、pure type system への道を lambda cube に沿ってたどることとなる。
このように、型付きラムダ計算を一度導入してしまえば、
後は単なる拡張により、言語がより豊かなものとなっていくことが見てとれる。
ぜひとも、Types and Programming Langages を読み、チャレンジして欲しい。
参考文献
- [HoTT] Homotopy Type Theory
- [Pierce] Types and Programming Languages
- [Aho 原田賢一訳] コンパイラ 原理技法ツール
- [E.Riehl, D. Verity] elements of ∞-category theory
- [O.Carmello] Sheaves, Sites, and Toposes
- [Kashiwara, Schapira] categories and sheaves