前書き
『珠玉のプログラミング』コラム8では、部分配列の和の最大を求めるアルゴリズムが説明されています。
最初に読んだのは10年も前ですが、未だ読み返す度に「どうして?」「凄い!」と感慨を持ちます。しかしそれを何度も繰り返してしまうのは自分の中で消化しきれていない証拠でしょう。少なくとも手元の道具箱に入っていない。
という訳で、理解を深めるため自分への説明を試みます(チラ裏失敬)。
問題
珠玉のプログラミング(*)から、問題と線形のアルゴリズム(O(n))の擬似コード部分を引用します。
問題部分の引用(p96)
今、n要素の浮動小数点数の配列xを入力とし、配列xの連続した要素(部分配列)でその和が最大になるものを見つけ、その和を出力とします。たとえば、入力配列が次のような10要素のものであった場合、
+---+---+---+---+---+---+---+---+---+---+ | 31|-41| 59| 26|-53| 58| 97|-93|-23| 84| +---+---+---+---+---+---+---+---+---+---+ ↑ ↑ 2 6
このプログラムの出力はx[2..6]の和で187です。
最初にこれを読んだ時、O(n^2)のアルゴリズムまでは自力で考え付きました。次の、O(n log n)である「分割して征服」は机上で組み立てるまではできましたが、実装は試しませんでした。諦めて次のページを眺めると、
アルゴリズム4の擬似コードの引用(p102)
maxsofar = 0 maxendinghere = 0 for i = [0, n) /* 不変な表明:maxsofarとmaxendinghereは x[0..i-1]について成立している */ maxendinghere = max(maxendinghere + x[i], 0) maxsofar = max(maxsofar, maxendinghere)
なんとループが1つしかありません。O(n)のアルゴリズムです。ホントかよ!
それが正しい(らしい)ことに驚きました。そして導く方法について理解したところで再び驚愕しました。
どうしてこれが正しいのか真に理解したい。
可視化してみた
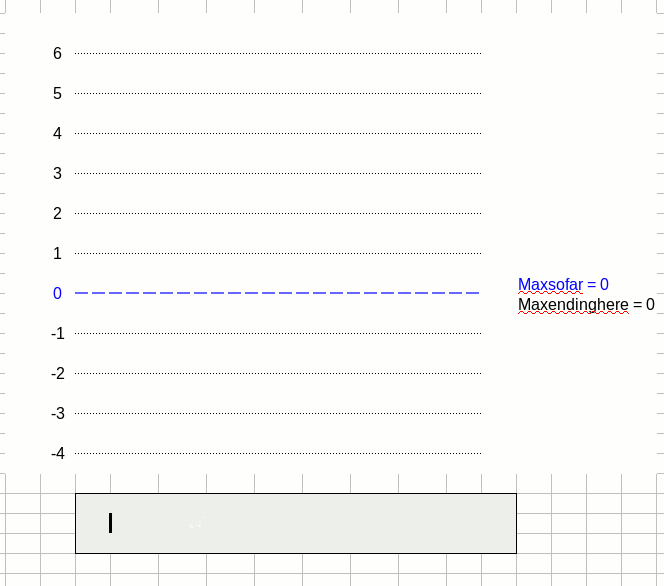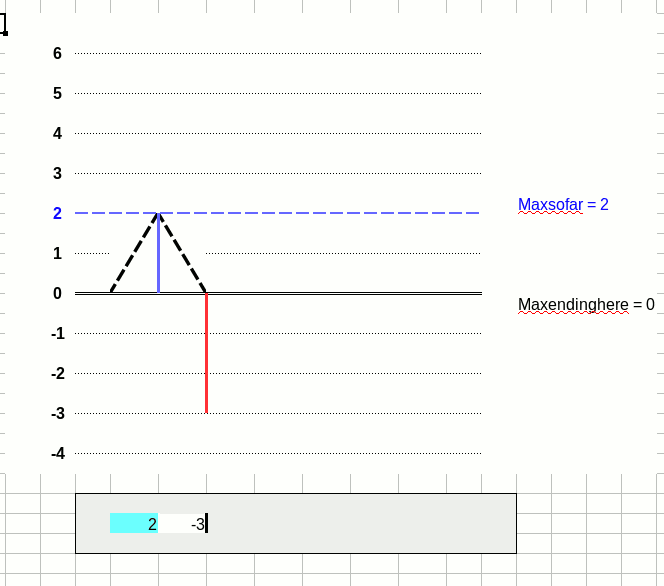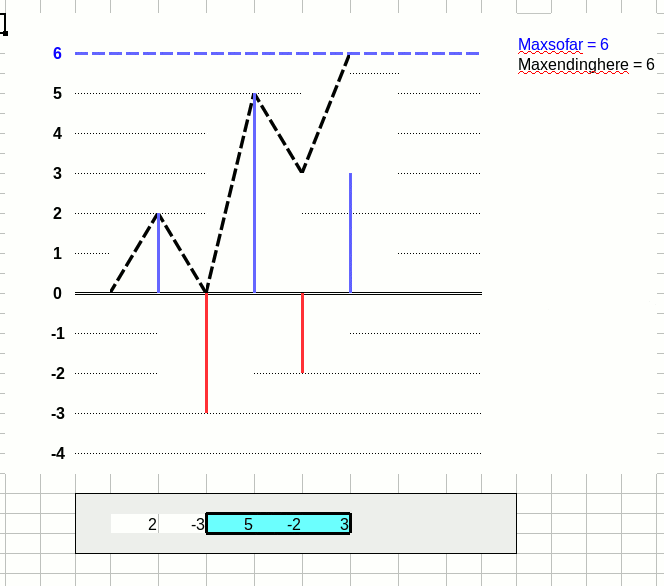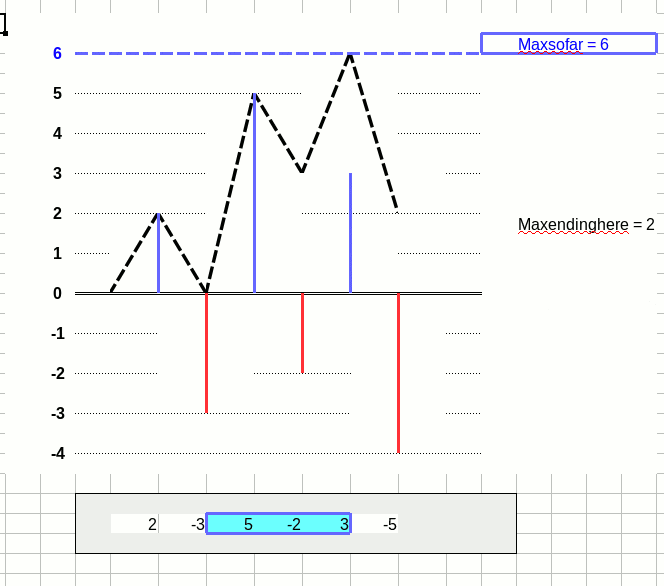
データは単純化しました。
x = {2, -3, 5, -2, 3, -4}
上はループ各回のmaxsofarとmaxendinghereの値をグラフ化したもの。
下は、それぞれmaxsofarとmaxendinghereの範囲を表しています。
maxsofarの範囲 :青塗り
maxendinghereの範囲:枠囲み(空配列の時は最右に|)
考え方を噛み砕く
説明では、
『 x[0..i-1]の範囲で答えがわかっているとき x[0..i]の範囲へ拡張するにはどうすればいいか』を考える
とあり、また
『i要素中で要素の和が最大になる部分配列は、i-1要素中で要素の和が最大になる部分配列か、i番要素で終わる部分配列中で要素の和が最大になるもののどちらか』
となっています。
まずこれを理解します。
『i-1要素中で要素の和が最大になる部分配列』が『i要素中で要素の和が最大になる部分配列』である場合については、納得です。逆に『x[i]は解を更新しない』と言えます。
後者の『i番要素で終わる部分配列中で要素の和が最大になるもの』が『i要素中で要素の和が最大になる部分配列』である場合については容易に気が付けないかも知れません。よく考えてみれば、 x[0..i-1] の範囲を x[0..i] にして『解が変わる』なら、解には x[i] が必ず関わってきます。そうでなければ、x[0..i-1] の解と x[0..i] で解が同じになるからです。よって『x[i]を含めると、部分配列の和の最大値が変わるなら、その部分配列はx[i]を含んでいるはず』までは理解。
ここまでで帰納法となる条件は理解できますが、次が厄介です。
帰納法として考えるには繰り返しの最後で必ず『不変な表明』が成り立たなければなりません。それが崩れると、任意のiについてx[0..i-1]からx[0..i]へ拡張する事ができず、帰納法になりません。つまりmaxendinghereは『x[0..i]で、x[i]を含む部分配列の和の最大』を常に成立させる必要があります。
『x[i]を含み、和が最大となる部分配列』とは
- 『x[i-1]を含む部分配列にx[i]を結合した部分配列』の和が正のとき、その部分配列
- 『x[i-1]を含む部分配列にx[i]を結合した部分配列』の和が負のとき、『空配列』(つまり最大は空配列の和である0)
2点目が難しい。
難しさの原因として、まずは『空配列も部分配列のひとつ』『空配列は和が0』である事を忘れないようにしないとダメ(すぐ定義を忘れる。。)。
もう一つ、『x[i]で終わる部分配列中で要素の和が最大になるもの』は空配列であり得るということ。『x[i]で終わる』と言っているのに、それが『空配列』なのは混乱する。自然言語ではなく、いちど形式言語(数式)で整理した方が分かりやすいかもしれません。
同じような問題に出会った時のため
- x[0..i-1]の解から、x[0..i]の解を導けないか
- そのための条件は何か。
- 不変な表明があるか
補. 定義を忘れるな
練習1 配列の和
配列の和(但し空配列の和は0)。
(1). x[0..i-1]の解から、x[0..i]の解を導けないか
sum(空配列)は0
sum(x[0..i-1])からsum(x[0..i])を導ける(はず)
(2).そのための条件は何か。
sum(x[0..i-1])にx[i]を足すとsum(x[0..i])になる
(3). 不変な表明があるか
sum(x[0..i-1])は[0..i-1]の和である
結論:配列の和はO(n)のアルゴリズムで計算できる
練習2 配列中の正の要素の和
配列中の正の要素の和(但し空配列の和は0)
(1). x[0..i-1]の解から、x[0..i]の解を導けないか
sum_positive(空配列)は0
sum_positive(x[0..i-1])からsum_positive(x[0..i])を導ける(はず)
(2).そのための条件は何か。
x[i]が正(0含む)の時、sum_positive(x[0..i])は、sum_positive(x[0..i-1]) + x[i]
x[i]が負の時、 sum_positive(x[0..i])は、sum_positive(x[0..i-1]) + 0
(3). 不変な表明があるか
sum_positive(x[0..i-1])は、x[0..i-1]の正の要素の和
結論:配列の和はO(n)のアルゴリズムで計算できる
擬似コードで実装してみる
ループ
sum_positive = 0
for i = [0..n)
/* 不変な表明: sum_positiveはx[0..i-1]について成立している */
if x[i] >= 0
/* sum_positiveはx[0..i-1]について成立している。x[i] >= 0 */
sum_positive += x[i]
/* sum_positiveはx[0..i]について成立している */
else
/* sum_positiveはx[0..i-1]について成立している。x[i] < 0 */
sum_positive += 0
/* sum_positiveはx[0..i]について成立している */
再帰(iが-1のときは空配列を示す)
sum_positive(x, i)
/* 不変な表明: sum_positiveはx[0..i]について成立している */
if i == -1
/* sum_positiveがx[0..i-1]について成立しているなら、sum_positiveはx[0..i]について成立している。iは-1 (つまりxは空配列) */
return 0
/* sum_positiveはx[0..i]について成立している。xは空配列(つまりsum_positive(空配列)で値は0) */
if x[n-1] >= 0
/* sum_positive が x[0..i-1] について成立しているなら、sum_positive は x[0..i] について成立している。x[i] >= 0 */
return sum_positive(x, i-1) + x[i]
/* sum_positive が x[0..i-i] について成立しているなら、sum_positive は x[0..i] について成立している
else
/* sum_positive が x[0..i-1] について成立しているなら、sum_positive はx[0..i] について成立している。x[i] < 0 */
return sum_positive(x, i-1) + 0
/* sum_positive が x[0..i-i] について成立しているなら、sum_positive はx[0..i] について成立している */
sum_positive(x, length(x)-1)
でもこれ、『配列中から正の要素を抜き出す』『配列の和を計算する』に分けた方が、正しさを示すには楽だなと。時代はやはり関数型プログラミング?
書籍
AMAZON
珠玉のプログラミング 本質を見抜いたアルゴリズムとデータ構造
よもやま話
『6歳の子供に説明できなければ、理解したとは言えない。』アルベルト・アインシュタイン
先生、無理です!
『プログラミング初心者でもなんとなく理解できる』まで妥協しました。
きっと本当には理解できていない、ぐぬぬ・・・。