Rubyで使用されている乱数の均等分布について(メルセンヌ・ツイスタ)

メルセンヌ・ツイスタとは、通常よりランダムな(周期の長い)値を生成する方法らしい（詳細はWikipedia）略してMT

Rubyは標準でこれを採用しているみたい
値が均等に分布しているのか、とりあえずこんな感じで100万回の平均をとってみた

MAX_VAL = 101
REP_CNT = 10**6

sum = 0.0
prng = Random.new(Random.new_seed)
(0...REP_CNT).each{|idx|
	p sum = (sum*idx + prng.rand(MAX_VAL))/(idx+1)
}

結果は
50.036861963137966

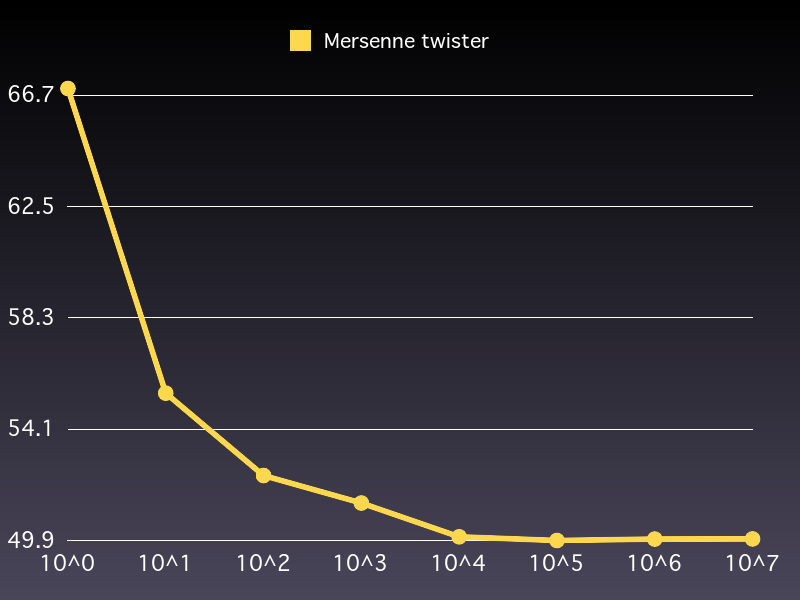
収束していることはわかったけど、どうやって収束していっているかを分かりやすくするためグラフを出してみた

# -*- encoding: utf-8 -*-

require 'rubygems'
require 'gruff'

FONT = "/Library/Fonts/Osaka.ttf"
MAX_VAL = 101
GRAPH_NUM = 7
REP_CNT = 10**GRAPH_NUM

graph_point = Array.new(GRAPH_NUM)

avg, rec_cnt = 0.0, 0
prng = Random.new(Random.new_seed)
(0...REP_CNT).each{|idx|
	avg = (avg*idx + prng.rand(MAX_VAL))/(idx+1)
	if 10**rec_cnt-1 == idx
		graph_point[rec_cnt] = avg
		rec_cnt += 1
	end
}

p graph_point

g = Gruff::Line.new
g.font = FONT

(0..graph_point.length).each{|idx|
	g.labels[idx] = "10^#{idx}"
}

g.data("Mersenne twister", graph_point)
g.write('MT.png')

実際の値は
10^0:67.0
10^1:55.5
10^2:52.39
10^3:51.352
10^4:50.076400000000085
10^5:49.93751999999963
10^6:49.99161700000036
10^7:49.99675620000007

50に近づいていってることがわかった
均等に分布している事が分かったので安心