線形
-
ざっくり比例
-
回帰問題
ある入力(離散あるいは連続地)から出力(連続値)を予測する問題
直線で予測→線形回帰
曲線で予測→非線形回帰
- 回帰で扱うデータ
入力(各要素を説明変数または特徴量と呼ぶ)
- m次元のベクトル(m=1場合はスカラ)
出力(目的変数) - スカラー値(目的変数)
説明変数
X=(x_1,x_2,...,x_m)^T \in \mathbb{R}^m
目的変数
y\in\mathbb{R}^1
線形回帰モデル
- 回帰問題を解くための機械学習モデルの一つ
- 教師あり学習(教師データから学習)
- 入力とm次元パラメータの線形結合を出力するモデル
パラメータ
X=(x_1,x_2,...,x_m)^T \in \mathbb{R}^m
線形結合
\hat{y} = w^Tx+w_0=\sum_{j=1}^{m}w_jx_j+w_0
- 説明変数が1次元の場合(m=1)の場合
単回帰モデルと呼ぶ
- データへの仮定
データは回帰直線に誤差が加わり観測されていると仮定
-連立方程式
それぞれのデータをモデル式へ当てはめるとn個の式が導出される。

- 説明変数がm次元の場合

- データの分割
学習用データ:機械学習モデルの学習に利用するデータ
検証用データ:学習済みモデルの精度を検証するためのデータ
- なぜ分割するのか
モデルの汎化性能(Generalization)を測定するため
データへの当てはまりの良さではなく、未知のデータに対してどれくらい精度が高いかを測りたい。
線形回帰モデルのパラメータは最小二乗法で推定
- 平均二乗誤差(残差平方和)
データとモデル出力の二乗誤差の和
パラメータのみに依存する関数
データは既知の値でパラメータのみ未知
- 最小二乗法
学習データの平均二乗誤差を最小とするパラメータを探索
学習データの平均二乗誤差の最小化は、その勾配が0になる点を求めれば良い
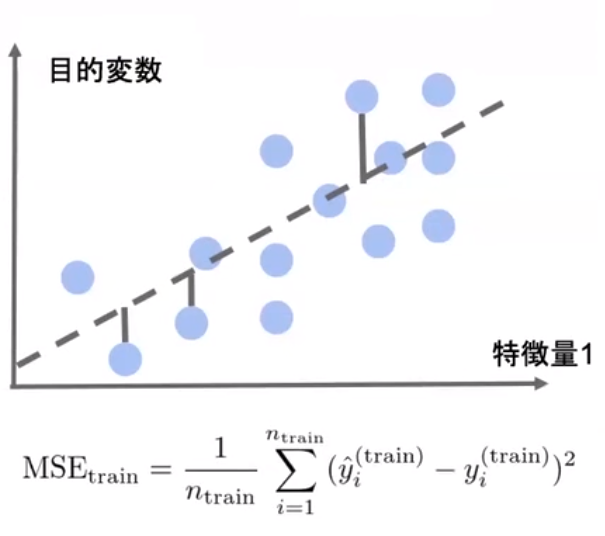
*二乗損失は一般に外れ値に弱い→Huber損失,Tukey損失
- MSEを最小にするようなW(m次元)
\hat{w}=\underset{w \in \mathbb{R}}{\textrm{arg minMSE_tarin}}
MSEをWに関して微分したものが0となるWの点を求める
\frac{\partial}{\partial w}MSE_{tarin}=0
回帰係数
\hat{w} = (X^{(train)T}X^{(train)})^{-1}X^{(train)T}y^{(train)}
予測値
\hat{y} = \underset{n_{new×m+1}}{X}(X^{(train)T}X^{(train)})^{-1}X^{(train)T}y^{(train)}
ハンズオン
ボストンの住宅データデットを線形回帰モデルで分析