非階層クラスター分析のk-means法をPHPで作ってみた

非階層クラスター分析で代表的な手法のk-means法は、pythonのライブラリに存在したり、統計ソフトに標準機能として搭載されていることが多く、なじみの多い手法のようですが、実際のアルゴリズムを確認するために、（慣れている）PHPで作ってみました。

k-means法のアルゴリズムの理解は、こちらがわかりやすいです。

ソースは以下の通りです。

点を2次元平面に点在させて、それらのクラスターに分けます。
完全にランダムに配置させると、クラスター化の初期値依存が高くなるため、敢えていくつかの場所に集中して配置させるようにしました。

<?php

$max = 500; //領域の大きさ
$margin = 50; //ランダムの配置するときの中心からの範囲
$dot_num_per_center = 30; //１中心点に配置するときの点の数
$center_num = 4; //中心点の数
$action_num = 5; //k-means実行回数

//点の配置
print "①この下の表が配置した点です。";
$dots = array();
print "<table>";
for ($i = 1; $i <= $center_num; $i++) {
    //中心点の位置をランダムに決める
    $center_x = rand($margin, $max - $margin);
    $center_y = rand($margin, $max - $margin);
    for ($j = 1; $j <= $dot_num_per_center; $j++) {
        //中心点を中心にmarginの範囲で点を決める
        $x = rand($center_x - $margin, $center_x + $margin);
        $y = rand($center_y - $margin, $center_y + $margin);
        $dots[] = ["x" => $x, "y" => $y];
        print "<tr><td>{$x}</td><td>{$y}</td></tr>";
    }
}
print "</table>";

//初期の重心を適当に決める（適当すぎて重心候補から外れてエラーになることがある）
$gravity = [];
for ($i = 1; $i <= $center_num; $i++) {
    $gravity[$i]["x"] = rand($margin, $max - $margin);
    $gravity[$i]["y"] = rand($margin, $max - $margin);
}

//k-means実行
for($num = 1; $num <= $action_num; $num++)
{
    //各点の一番近い重心を決める
    foreach ($dots as $dot_key => $dot) {
        $min_length = 0;
        for ($i = 1; $i <= $center_num; $i++) {
            $length = calc_length($gravity[$i]["x"], $gravity[$i]["y"], $dot["x"], $dot["y"]);
            if($min_length === 0 || $min_length > $length) {
                $min_length = $length;
                $dots[$dot_key]["gravity_number"] = (int)$i;
            }
        }
    }

    //各重心の点の重心を再計算する
    $gravity = [];
    $count = [];
    foreach ($dots as $dot_key => $dot) {
        if(!isset($gravity[$dot["gravity_number"]]["x"])) $gravity[$dot["gravity_number"]]["x"] = 0;
        $gravity[$dot["gravity_number"]]["x"] += $dot["x"];
        if(!isset($gravity[$dot["gravity_number"]]["y"])) $gravity[$dot["gravity_number"]]["y"] = 0;
        $gravity[$dot["gravity_number"]]["y"] += $dot["y"];

        //核にある点の数
        if(!isset($count[$dot["gravity_number"]]))$count[$dot["gravity_number"]] = 0;
        $count[$dot["gravity_number"]]++;
    }

    for ($i = 1; $i <= $center_num; $i++) {
        if(isset($gravity[$i]["x"]))$gravity[$i]["x"] /= $count[$i];
        if(isset($gravity[$i]["y"]))$gravity[$i]["y"] /= $count[$i];
    }
}

print "<br /><br /><br />②以下がクラスターに分けたデータです";

//それぞれの重心の点を表示する
print "<table>";
foreach ($dots as $dot_key => $dot) {
    print"<tr><td>{$dot["x"]}".(str_repeat("</td><td>", (int)$dot["gravity_number"])).$dot["y"]."</td></tr>";
}
print "</table>";

//長さを求める
function calc_length($x1, $y1, $x2, $y2)
{
    return sqrt(pow($x1 - $x2, 2) + pow($y1 - $y2, 2));
}

データの見方

上記PHPを実行すると、上下に2つの表が出力します。（①②と表示しています）

データの点在確認

①はデータの点在を確認します。エクセルに貼り付けて、「散布図」にて確認出来ます。

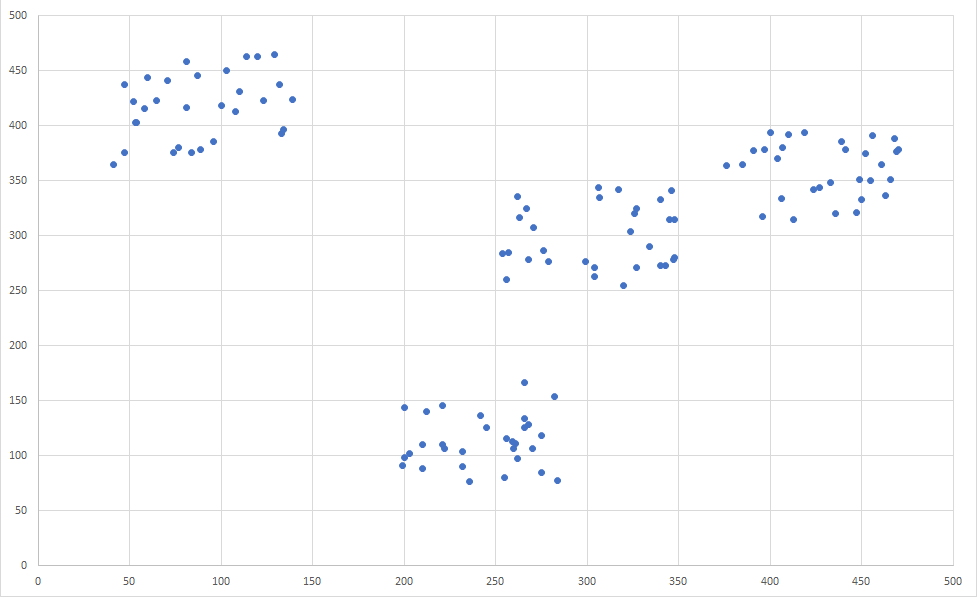
クラスターの確認

②はクラスター分けされた状態を確認できます。同じくエクセルに貼り付けて、「散布図」にて確認出来ます。

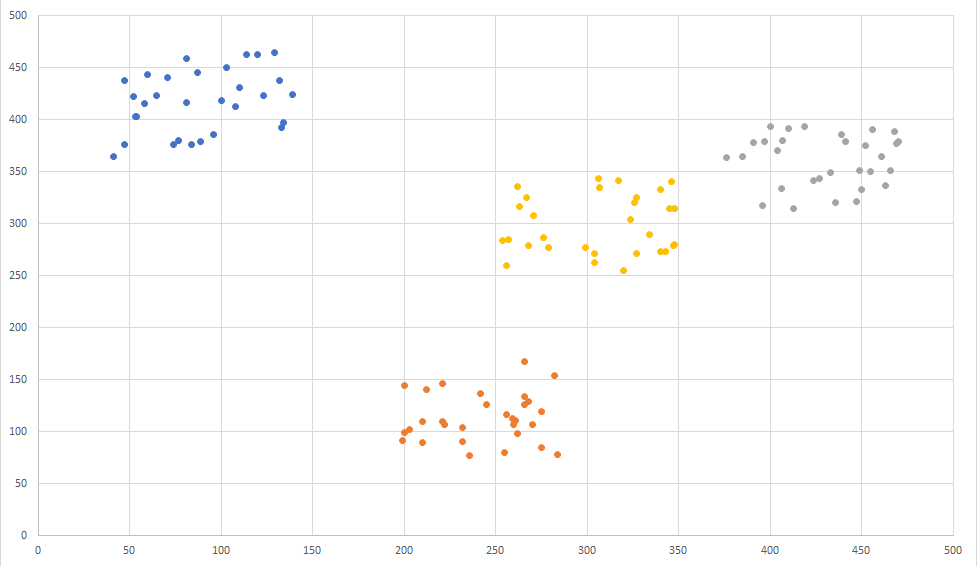
課題

仮に決めた重心が完全ランダムですので、データの点在から離れすぎてエラーとなることがあります。。。
その時は、再度実行して下さい。
実際のk-means法では、仮決めの重心はデータの点在状況に応じて、ある程度領域を限定するものだとわかりました。