え?
$$ L = K\frac{{\mu _0 S N^2 }}{{h}} $$
$$ S=\pi a^2 $$
$$ dA\left( {z,\zeta ,\theta } \right) = \frac{{\mu _0 }}{{4\pi }} , \frac{{Jc \ d\zeta }}{{\tau \left( {\zeta - z,\theta } \right)}} $$
$$ Jc = \frac{{I , N}}{h} $$
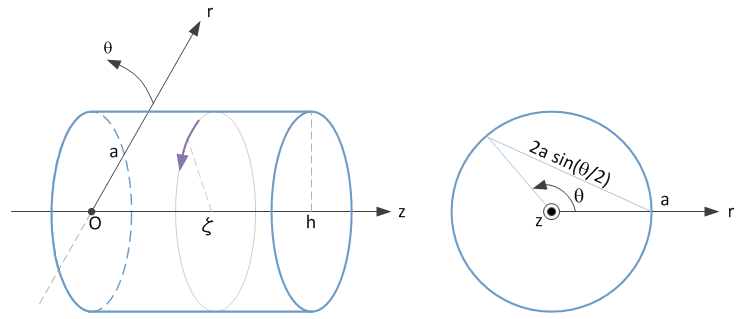
$$ \tau \left( {x,\theta } \right) = \sqrt {x^2 + 4a^2 \sin ^2 \frac{\theta }{2}} $$
\begin{align*}
\eqalign{
\Phi c\left( {z,\zeta } \right) &= 2\pi a\int_\alpha ^{2\pi + \alpha } {dA\left( {z,\zeta ,\theta } \right)\cos \theta ds} \cr
& \Rightarrow 2\pi a\int_{n\pi }^{2\pi + n\pi } {dA\left( {z,\zeta ,\theta } \right)\cos \theta ds} \cr
& = 4\pi a\int_{n\pi }^{\pi + n\pi } {dA\left( {z,\zeta ,\theta } \right)\cos \theta ds} \cr}
\end{align*}
$$ ds = a , d\theta $$
$$ \Phi \left( z \right) = \int_{\zeta = 0}^{\zeta = h } {\Phi c\left( {z,\zeta } \right) } $$
$$ \Phi m = \int_0^h {\Phi \left( z \right)N\frac{{dz}}{h}} $$
$$ L = \frac{{\Phi m}}{I} $$
$ $
\begin{align*}
\eqalign{
K & = \frac{h}
{{\mu _0 SN^2 }}L = \frac{h}
{{\mu _0 SN^2 }} \cdot \frac{{\Phi m}}
{I} \cr
& = \frac{h}
{{\mu _0 \pi a^2 N^2 I}}\int_0^h {\int_0^h {4\pi a\int_{n\pi }^{\pi + n\pi } {\frac{{\mu _0 }}
{{4\pi }}\frac{{Jc\cos \theta }}
{{\tau \left( {\zeta - z,\theta } \right)}}\;ds} } d\zeta \frac{N}
{h}dz} \cr
& = \frac{h}
{{\mu _0 \pi a^2 N^2 I}}\int_0^h {\int_0^h {4\pi a\int_{n\pi }^{\left( {n + 1} \right)\pi } {\frac{{\mu _0 }}
{{4\pi }} \cdot \frac{{I\;N\;a\;\cos \theta }}
{{h\;\tau \left( {\zeta - z,\theta } \right)}}\;d\theta } \;} d\zeta \frac{N}
{h}dz} \cr
& = \frac{1}
{{\pi h}}\int_0^h {\int_0^h {\int_{n\pi }^{\left( {n + 1} \right)\pi } {\frac{{\cos \theta }}
{{\tau \left( {\zeta - z,\theta } \right)}}\;d\theta } \;} d\zeta dz} \cr}
\end{align*}
$ $
\begin{align*}
& \phi + \frac{\pi }{2} = \frac{\theta }{2} \\
& \theta = 2\phi + \pi \\
& \sin \frac{\theta }{2} = \cos \phi \\
& \tau \left( {x,\theta } \right) = \sqrt {x^2 + 4a^2 \sin ^2 \frac{\theta }{2}} \\
& \ ~~~~ = \sqrt {x^2 + 4a^2 \cos ^2 \phi } = \sqrt {x^2 + 4a^2 - 4a^2 \sin ^2 \phi } \\
& \ ~~~~ = \sqrt {x^2 + 4a^2 } \sqrt {1 - \frac{{4a^2 }}{{x^2 + 4a^2 }}\sin ^2 \phi } \\
& w_1 = \frac{{2a}}{{\sqrt {\left( {\zeta - z} \right)^2 + 4a^2 } }} \\
& \tau \left( {\zeta - z,2\phi + \pi } \right) = 2a\;w_1 ^{ - 1} \sqrt {1 - w_1 ^2 \sin ^2 \phi } \\
\end{align*}
$ $
\begin{align*}
\eqalign{
& \int_{n\pi }^{\left( {n + 1} \right)\pi } {\frac{{\cos \theta }}
{{\tau \left( {\zeta - z,\theta } \right)}}\;d\theta } = \int_{n\pi = 2\phi + \pi }^{\left( {n + 1} \right)\pi = 2\phi + \pi } {\frac{{ - \cos 2\phi }}
{{\tau \left( {\zeta - z,2\phi + \pi } \right)}}\;2d\phi } \cr
& = \int_{n\pi - \pi = 2\phi }^{n\pi = 2\phi } {\frac{{ - 2\cos 2\phi }}
{{2a\;w_1 ^{ - 1} \sqrt {1 - w_1 ^2 \sin ^2 \phi } }}\;d\phi } = - \frac{{w_1 }}
{a}\int_{\phi = \pi \frac{{n - 1}}
{2}}^{\phi = \frac{{n\pi }}
{2}} {\frac{{1 - 2\sin ^2 \phi }}
{{\sqrt {1 - w_1 ^2 \sin ^2 \phi } }}\;d\phi } \cr
& = - \frac{1}
{{a\;w_1 }}\int_0^{\frac{\pi }
{2}} {\frac{{w_1 ^2 - 2w_1 ^2 \sin ^2 \phi }}
{{\sqrt {1 - w_1 ^2 \sin ^2 \phi } }}\;d\phi } = - \frac{1}
{{a\;w_1 }}\int_0^{\frac{\pi }
{2}} {\frac{{2 - 2w_1 ^2 \sin ^2 \phi + w_1 ^2 - 2}}
{{\sqrt {1 - w_1 ^2 \sin ^2 \phi } }}\;d\phi } \cr
& = - \frac{1}
{{a\;w_1 }}\int_0^{\frac{\pi }
{2}} {\left( {2\sqrt {1 - w_1 ^2 \sin ^2 \phi } + \frac{{w_1 ^2 - 2}}
{{\sqrt {1 - w_1 ^2 \sin ^2 \phi } }}} \right)\;d\phi } \cr
& = - \frac{1}
{{a\;w_1 }}\left\{ {2E\left( {w_1 } \right) + \left( {w_1 ^2 - 2} \right)K\left( {w_1 } \right)} \right\} \cr
& = \frac{1}
{a}\left\{ {\left( {\frac{2}
{{w_1 }} - w_1 } \right)K\left( {w_1 } \right) - 2\frac{{E\left( {w_1 } \right)}}
{{w_1 }}} \right\} \cr}
\end{align*}
$$ K\left( t \right) = \int_{0}^{\frac{\pi }{2}} {\frac{1}{{\sqrt {1 - t^2 \sin ^2 \phi } }};d\phi } \
E\left( t \right) = \int_0^{\frac{\pi }{2}} {\sqrt {1 - t^2 \sin ^2 \phi } ;d\phi } $$
\begin{align*}
K &= \frac{1}{{\pi h}}\int_0^h {\int_0^h {\int_{n\pi }^{(n+1)\pi } {\frac{{\cos \theta }}{{\tau \left( {\zeta - z,\theta } \right)}}\;d\theta } } d\zeta dz} \\
&= \frac{1}{{\pi ah}}\int_0^h {\int_0^h {\left\{ {\left( {\frac{2}{{w_1 }} - w_1 } \right)K\left( {w_1 } \right) - \frac{2}{{w_1 }}E\left( {w_1 } \right)} \right\}d\zeta } dz} \\
\end{align*}
$$ w_1 = \frac{{2a}}{{\sqrt {\left( {\zeta - z} \right)^2 + 4a^2 } }} \\
\left( {\zeta - z} \right)^2 + 4a^2 = 4a^2 w_1 ^{ - 2} \\
\left( {\zeta - z} \right)^2 = 4a^2 w_1 ^{ - 2} - 4a^2 = 4a^2 \left( {w_1 ^{ - 2} - 1} \right) \\
\zeta - z = \pm 2aw_1 ^{ - 1} \sqrt {1 - w_1 ^2 } \\
2\left( {\zeta - z} \right) = - 8a^2 w_1 ^{ - 3} \frac{{dw_1 }}{{d\zeta }} \\
- \frac{{w_1 ^3 }}{{4a^2 }}\left( {\zeta - z} \right) = \frac{{dw_1 }}{{d\zeta }} \\
- \frac{{w_1 ^3 }}{{4a^2 }}\left( {\zeta - z} \right)^2 = \frac{{dw_1 }}{{d\zeta }}\left( {\zeta - z} \right) \\
\left( {\zeta - z} \right)\frac{{dw_1 }}{{d\zeta }} = - \frac{{w_1 ^3 }}{{4a^2 }} \cdot 4a^2 \left( {w_1 ^{ - 2} - 1} \right) = - w_1 \left( {1 - w_1 ^2 } \right) \ $$
\begin{align*}
& \left( {\zeta - z} \right)Fa = \int {\frac{d}{{d\zeta }}\left\{ {\left( {\zeta - z} \right)Fa} \right\}d\zeta } = \int {\left\{ {Fa + \left( {\zeta - z} \right)\left( {\frac{d}{{d\zeta }}Fa} \right)} \right\}d\zeta } \\
&= \int {\left[ {Fa + \left\{ {\left( {\zeta - z} \right)\frac{{dw_1 }}{{d\zeta }}} \right\}\left( {\frac{{dFa}}{{dw_1 }}} \right)} \right]d\zeta } \\
&= \int {\left\{ {Fa - w_1 \left( {1 - w_1 ^2 } \right) \cdot \frac{{dFa}}{{dw_1 }}} \right\}d\zeta } \\
\end{align*}
\begin{align*}
& y = \sqrt {1 - x^2 } \\
& \frac{{dy}}{{dx}} = \frac{1}{2}y^{ - 1} \left( { - 2x} \right) = - xy^{ - 1} \\
& \frac{{dK\left( x \right)}}{{dx}} = - \frac{{K\left( x \right)}}{x} + \frac{{E\left( x \right)}}{{xy^2 }} = x^{ - 1} y^{ - 2} \left\{ { - y^2 K\left( x \right) + E\left( x \right)} \right\} \\
& \frac{{dE\left( x \right)}}{{dx}} = - \frac{{K\left( x \right)}}{x} + \frac{{E\left( x \right)}}{x} = x^{ - 1} \left\{ { - K\left( x \right) + E\left( x \right)} \right\} \\
\end{align*}
\begin{align*}
\frac{{d\left\{ {x^n K\left( x \right)} \right\}}}{{dx}} &= x^{n - 1} \left\{ {\left( {n - 1} \right)K\left( x \right) + x^{ - 1} y^{ - 2} E\left( x \right)} \right\} \\\
\frac{{d\left\{ {x^n E\left( x \right)} \right\}}}{{dx}} &= x^{n - 1} \left\{ { - K\left( x \right) + \left( {n + 1} \right)E\left( x \right)} \right\} \\
\end{align*}
\begin{align*}
\begin{array}{*{20}c}
f & {f'} & f & {f'} \\
{x^2 K} & {xK + xy^{ - 2} E} & {x^2 E} & { - xK + 3xE} \\
{xK} & {y^{ - 2} E} & {xE} & { - K + 2E} \\
K & { - x^{ - 1} K + x^{ - 1} y^{ - 2} E} & E & { - x^{ - 1} K + x^{ - 1} E} \\
{x^{ - 1} K} & { - 2x^{ - 2} K + x^{ - 2} y^{ - 2} E} & {x^{ - 1} E} & { - x^{ - 2} K} \\
{x^{ - 2} K} & { - 3x^{ - 3} K + x^{ - 3} y^{ - 2} E} & {x^{ - 2} E} & { - x^{ - 3} K - x^{ - 3} E} \\
{x^{ - 3} K} & { - 4x^{ - 4} K + x^{ - 4} y^{ - 2} E} & {x^{ - 3} E} & { - x^{ - 4} K - 2x^{ - 4} E} \\
\end{array}
\end{align*}
\begin{align*}
& \left( {\frac{2}{x} - x} \right)K - 2\frac{E}{x} = 2x^{ - 1} K - xK - 2x^{ - 1} E \\
&= x^{ - 1} \left( {2 - x^2 } \right)K - 2x^{ - 1} E \\
&= x^{ - 1} \left\{ {\left( {1 + y^2 } \right)K - 2E} \right\} \\
&= - xy^2 \cdot x^{ - 2} y^{ - 2} \left\{ { - \left( {1 + y^2 } \right)K + 2E} \right\} \\
&= - xy^2 \left( { - x^{ - 2} y^{ - 2} K - x^{ - 2} K + 2x^{ - 2} y^{ - 2} E} \right) \\
&= x^{ - 1} K - xy^2 \left( { - x^{ - 2} K + 2x^{ - 2} y^{ - 2} E} \right) \\
&= x^{ - 1} K - xy^2 \left( { - 2x^{ - 2} K + x^{ - 2} y^{ - 2} E + 2x^{ - 2} K - x^{ - 2} y^{ - 2} E - x^{ - 2} K + 2x^{ - 2} y^{ - 2} E} \right) \\
&= x^{ - 1} K - xy^2 \left( {\frac{d}{{dx}}x^{ - 1} K + x^{ - 2} K + x^{ - 2} y^{ - 2} E} \right) \\
&= x^{ - 1} K - x^{ - 1} E - xy^2 \left( {\frac{d}{{dx}}x^{ - 1} K + x^{ - 2} K} \right) \\
&= x^{ - 1} K - x^{ - 1} E - xy^2 \left( {\frac{d}{{dx}}x^{ - 1} K - \frac{d}{{dx}}x^{ - 1} E} \right) \\
&= \frac{{K - E}}{x} - xy^2 \frac{d}{{dx}}\left( {\frac{{K - E}}{x}} \right) \\
\end{align*}
\begin{align*}
K &= \frac{1}{{\pi ah}}\int_0^h {\int_0^h {\left\{ {\left( {\frac{2}{{w_1 }} - w_1 } \right)K\left( {w_1 } \right) - \frac{2}{{w_1 }}E\left( {w_1 } \right)} \right\}d\zeta } dz} \\
&= \frac{1}{{\pi ah}}\int_0^h {\left[ {\left( {\zeta - z} \right)\frac{{K\left( {w_1 } \right) - E\left( {w_1 } \right)}}{{w_1 }}} \right]_{\zeta = 0}^{\zeta = h} dz} \\
& w_2 = \frac{{2a}}{{\sqrt {\left( {h - z} \right)^2 + 4a^2 } }},\;w_3 = \frac{{2a}}{{\sqrt {z^2 + 4a^2 } }} \\
& \left[ {\left( {\zeta - z} \right)\frac{{K\left( {w_1 } \right) - E\left( {w_1 } \right)}}{{w_1 }}} \right]_{\zeta = 0}^{\zeta = h} = \left( {h - z} \right)\frac{{K\left( {w_2 } \right) - E\left( {w_2 } \right)}}{{w_2 }} + z\frac{{K\left( {w_3 } \right) - E\left( {w_3 } \right)}}{{w_3 }} \\
K &= \frac{1}{{\pi ah}}\int_0^h {\left\{ {\left( {h - z} \right)\frac{{K\left( {w_2 } \right) - E\left( {w_2 } \right)}}{{w_2 }} + z\frac{{K\left( {w_3 } \right) - E\left( {w_3 } \right)}}{{w_3 }}} \right\}dz} \\
&= \frac{1}{{\pi ah}}\left\{ {\int_0^h {\left( {h - z} \right)\frac{{K\left( {w_2 } \right) - E\left( {w_2 } \right)}}{{w_2 }}dz} + \int_0^h {z\frac{{K\left( {w_3 } \right) - E\left( {w_3 } \right)}}{{w_3 }}dz} } \right\} \\
\end{align*}
\begin{align*}
& w_4 = \frac{{2a}}{{\sqrt {\left( {\eta - z} \right)^2 + 4a^2 } }} \\
& \eta - z = 4a^2 w_4 ^{ - 3} \frac{{dw_4 }}{{dz}} \\
& \left( {\eta - z} \right)dz = 4a^2 w_4 ^{ - 3} dw_4 \\
& \int {\left( {\eta - z} \right)\frac{{K\left( {w_4 } \right) - E\left( {w_4 } \right)}}{{w_4 }}dz} = \int {\frac{{K\left( {w_4 } \right) - E\left( {w_4 } \right)}}{{w_4 }} \cdot 4a^2 w_4 ^{ - 3} dw_4 } \\
& = 4a^2 \int {\frac{{K\left( {w_4 } \right) - E\left( {w_4 } \right)}}{{w_4 ^4 }}dw_4 } \\
\end{align*}
$$
k = \frac{{2a}}
{{\sqrt {h^2 + 4a^2 } }} = \cos{\left( \arctan{\frac{2a}{{h}}} \right)}
$$
$$
\eqalign{
& 1 + \left( {\frac{h}{{2a}}} \right)^2 = k^{ - 2} \cr
& \frac{h}{{2a}} = k^{ - 1} \sqrt {1 - k^2 } \cr}
$$
\begin{align*}
\eqalign{
K &= \frac{1}
{{\pi ah}}\left\{ {\int_0^h {\left( {h - z} \right)\frac{{K\left( {w_2 } \right) - E\left( {w_2 } \right)}}
{{w_2 }}dz} - \int_0^h {\left( {0 - z} \right)\frac{{K\left( {w_3 } \right) - E\left( {w_3 } \right)}}
{{w_3 }}dz} } \right\} \cr
& = \frac{{4a^2 }}
{{\pi ah}}\left\{ {\int_{z = 0}^{z = h} {\frac{{K\left( {w_2 } \right) - E\left( {w_2 } \right)}}
{{w_2 ^4 }}dw_2 } - \int_{z = 0}^{z = h} {\frac{{K\left( {w_3 } \right) - E\left( {w_3 } \right)}}
{{w_3 ^4 }}dw_3 } } \right\} \cr
& = \frac{{2k}}
{{\pi \sqrt {1 - k^2 } }}\left\{ {\int_k^1 {\frac{{K\left( {w_4 } \right) - E\left( {w_4 } \right)}}
{{w_4 ^4 }}dw_4 } - \int_1^k {\frac{{K\left( {w_4 } \right) - E\left( {w_4 } \right)}}
{{w_4 ^4 }}dw_4 } } \right\} \cr
& = \frac{{4k}}
{{\pi \sqrt {1 - k^2 } }}\int_k^1 {\frac{{K\left( {w_4 } \right) - E\left( {w_4 } \right)}}
{{w_4 ^4 }}dw_4 } \cr}
\end{align*}
\begin{align*}
\eqalign{
\int {\frac{{K - E}}
{{x^4 }}dx} &= \int {\frac{{\left( {1 - c_1 } \right)K + 2\left( {1 - c_1 } \right)E + c_1 K - E - 2\left( {1 - c_1 } \right)E}}
{{x^4 }}dx} \cr
& = - \left( {1 - c_1 } \right)\int { - \frac{{K + 2E}}
{{x^4 }}dx} + c_1 \int {\frac{K}
{{x^4 }}dx} - \left( {3 - 2c_1 } \right)\int {\frac{E}
{{x^4 }}dx} \cr
& = - \left( {1 - c_1 } \right)\frac{E}
{{x^3 }} - \left( {3 - 2c_1 } \right)\int {\frac{{\left( {1 - x^2 } \right)E}}
{{x^4 \left( {1 - x^2 } \right)}}dx} + c_1 \int {\frac{K}
{{x^4 }}dx} \cr
& = - \left( {1 - c_1 } \right)\frac{E}
{{x^3 }} - \left( {3 - 2c_1 } \right)\int {\frac{E}
{{x^4 \left( {1 - x^2 } \right)}}dx} + \left( {3 - 2c_1 } \right)\int {\frac{E}
{{x^2 \left( {1 - x^2 } \right)}}dx} + c_1 \int {\frac{K}
{{x^4 }}dx} \cr
& = - \left( {1 - c_1 } \right)\frac{E}
{{x^3 }} - \left( {3 - 2c_1 } \right)\int {\left\{ { - \frac{{4K}}
{{x^4 }} + \frac{E}
{{x^4 \left( {1 - x^2 } \right)}}} \right\}dx} + \left( {3 - 2c_1 } \right)\int {\frac{E}
{{x^2 \left( {1 - x^2 } \right)}}dx} + c_1 \int {\frac{K}
{{x^4 }}dx} - \left( {3 - 2c_1 } \right)\int {\frac{{4K}}
{{x^4 }}dx} \cr
& = - \left( {1 - c_1 } \right)\frac{E}
{{x^3 }} - \left( {3 - 2c_1 } \right)\frac{K}
{{x^3 }} + \left( {3 - 2c_1 } \right)\int {\frac{E}
{{x^2 \left( {1 - x^2 } \right)}}dx} + \left\{ {c_1 - 4\left( {3 - 2c_1 } \right)} \right\}\int {\frac{K}
{{x^4 }}dx} \cr}
\end{align*}
$$ 0 = c_1 - 4\left( {3 - 2c_1 } \right) = - 12 + 9c_1 ,;;c_1 = \frac{4}{3} $$
\begin{align*}
\eqalign{
\int {\frac{{K - E}}
{{x^4 }}dx} &= \frac{1}
{3}\frac{E}
{{x^3 }} - \frac{1}
{3}\frac{K}
{{x^3 }} + \frac{1}
{3}\int {\frac{E}
{{x^2 \left( {1 - x^2 } \right)}}dx} \cr
& = \frac{1}
{3}\frac{E}
{{x^3 }} - \frac{1}
{3}\frac{K}
{{x^3 }} + \frac{1}
{3}\int {\frac{E}
{{x^2 \left( {1 - x^2 } \right)}}dx} \cr
& = \frac{E}
{{3x^3 }} - \frac{K}
{{3x^3 }} + \frac{1}
{3}\int {\left\{ { - \frac{{2K}}
{{x^2 }} + \frac{E}
{{x^2 \left( {1 - x^2 } \right)}} + \frac{{2K}}
{{x^2 }}} \right\}dx} \cr
& = \frac{E}
{{3x^3 }} - \frac{K}
{{3x^3 }} + \frac{1}
{3}\left( {\frac{K}
{x} - 2\frac{E}
{x}} \right) = \frac{1}
{3}\left( {\frac{E}
{{x^3 }} - \frac{K}
{{x^3 }} + \frac{K}
{x} - 2\frac{E}
{x}} \right) \cr
& = -\left(
{ \frac{1}{{x^3 }} - \frac{1}{x}} \right) \frac{K}{3}
+ \left(
{ \frac{1}{{x^3 }} - \frac{2}{x}} \right) \frac{E}{3} \cr}
\end{align*}
\begin{align*}
\eqalign{
K & = \frac{{4k}}
{{\pi \sqrt {1 - k^2 } }}\int_k^1 {\frac{{K\left( {w_4 } \right) - E\left( {w_4 } \right)}}
{{w_4 ^4 }}dw_4 } \cr
& = \frac{{4k}}
{{\pi \sqrt {1 - k^2 } }}\left[ -{\left( { \frac{1}
{{w_4 ^3 }} - \frac{1}
{{w_4 }}} \right)\frac{{K\left( {w_4 } \right)}}
{3} + \left( {\frac{1}
{{w_4 ^3 }} - \frac{2}
{{w_4 }}} \right)\frac{{E\left( {w_4 } \right)}}
{3}} \right]_k^1 \cr
& = \frac{{4k}}
{{3\pi \sqrt {1 - k^2 } }}\left\{ -{\mathop {\lim }\limits_{x \to + 0} \left( { - \frac{1}
{{\left( {1 - x} \right)^3 }} + \frac{1}
{{1 - x}}} \right)K\left( {1 - x} \right) - 1 + \left( {\frac{1}
{{k^3 }} - \frac{1}
{k}} \right)K\left( k \right) - \left( {\frac{1}
{{k^3 }} - \frac{2}
{k}} \right)E\left( k \right)} \right\} \cr
& = \frac{{4k}}
{{3\pi \sqrt {1 - k^2 } }}\left\{ {-0 - 1 + \left( {\frac{1}
{{k^3 }} - \frac{1}
{k}} \right)K\left( k \right) - \left( {\frac{1}
{{k^3 }} - \frac{2}
{k}} \right)E\left( k \right)} \right\} \cr
& = \frac{4}
{{3\pi \sqrt {1 - k^2 } }}\left\{ {\left( {\frac{1}
{{k^2 }} - 1} \right)K\left( k \right) - \left( {\frac{1}
{{k^2 }} - 2} \right)E\left( k \right) - k} \right\} \cr}
\end{align*}