ゑ?
$$ L = K\frac{{\mu _0 S N^2 }}{{h}} $$
$$ S=\pi a^2 $$
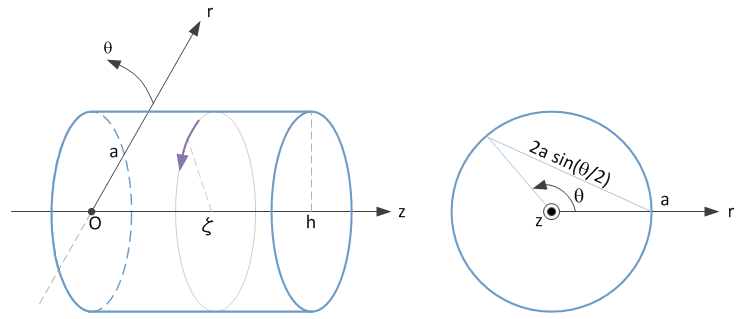
$$ dA\left( {z,\zeta ,\theta } \right) = \frac{{\mu _0 }}{{4\pi }} , \frac{{Jc \ d\zeta }}{{\tau \left( {\zeta - z,\theta } \right)}} $$
$$ Jc = \frac{{I , N}}{h} $$
$$ \tau \left( {x,\theta } \right) = \sqrt {x^2 + 4a^2 \sin ^2 \frac{\theta }{2}} $$
\begin{align*}
\Phi c\left( {z,\zeta } \right) = 2\pi a\int_\alpha ^{2\pi + \alpha } {dA\left( {z,\zeta ,\theta } \right)\cos \theta ds} \\
= 4\pi a\int_\psi ^{\pi + \psi } {dA\left( {z,\zeta ,\theta } \right)\cos \theta ds} \\
\end{align*}
$$ ds = a , d\theta $$
$$ \Phi \left( z \right) = \int_{\zeta = 0}^{\zeta = h } {\Phi c\left( {z,\zeta } \right) } $$
$$ \Phi m = \int_0^h {\Phi \left( z \right)N\frac{{dz}}{h}} $$
$$ L = \frac{{\Phi m}}{I} $$
$ $
\begin{align*}
K &= \frac{h}{{\mu _0 SN^2 }}L = \frac{h}{{\mu _0 SN^2 }} \cdot \frac{{\Phi m}}{I} \\
&= \frac{{h}}{{\mu _0 \pi a^2 N^2 I}}\int_0^h {\int_0^h {4\pi a\int_\psi ^{\pi + \psi } {\frac{{\mu _0 }}{{4\pi }}\frac{{Jc\cos \theta }}{{\tau \left( {\zeta - z,\theta } \right)}}\;ds} } d\zeta \frac{N}{h}dz} \\
&= \frac{{h}}{{\mu _0 \pi a^2 N^2 I}} \cdot \frac{{\mu _0 }}{{4\pi }}\int_0^h {\int_0^h {4\pi a\int_\psi ^{\pi + \psi } {\frac{{I\;N}}{h}\frac{{a\;\cos \theta }}{{\tau \left( {\zeta - z,\theta } \right)}}\;d\theta } \;} d\zeta \frac{N}{h}dz} \\
&= \frac{1}{{\pi h}}\int_0^h {\int_0^h {\int_\psi ^{\pi + \psi } {\frac{{\cos \theta }}{{\tau \left( {\zeta - z,\theta } \right)}}\;d\theta } \;} d\zeta dz} \\
\end{align*}
$ $
\begin{align*}
\eqalign{
& \phi + \frac{\pi }
{2} = \frac{\theta }
{2} \cr
& \theta = 2\phi + \pi \cr
& d\theta = 2d\phi \cr
& \sin \frac{\theta }
{2} = \cos \phi \cr
& \tau \left( {x,\theta } \right) = \sqrt {x^2 + 4a^2 \sin ^2 \frac{\theta }
{2}} = \sqrt {x^2 + 4a^2 \cos ^2 \phi } \cr}
\end{align*}
\begin{align*}
\eqalign{
K &= \frac{1}
{{\pi h}}\int_0^h {\int_0^h {\int_{n\pi }^{\left( {n + 1} \right)\pi } {\frac{{\cos \theta }}
{{\tau \left( {\zeta - z,\theta } \right)}}\;d\theta } \;} d\zeta dz} \cr
& = \frac{1}
{{\pi h}}\int_{n\pi }^{\left( {n + 1} \right)\pi } {\cos \theta \int_0^h {\int_0^h {\frac{1}
{{\sqrt {\left( {\zeta - z} \right)^2 + 4a^2 \sin ^2 \frac{\theta }
{2}} }}} d\zeta dz} d\theta } \cr
& = \frac{1}
{{\pi h}}\int_{n\pi = 2\phi + \pi }^{\left( {n + 1} \right)\pi = 2\phi + \pi } {\left( { - \cos 2\phi } \right)\int_0^h {\int_0^h {\frac{1}
{{\sqrt {\left( {\zeta - z} \right)^2 + 4a^2 \cos ^2 \phi } }}} d\zeta dz} \;2d\phi } \cr
& = - \frac{2}
{{\pi h}}\int_{\phi = \left( {n - 1} \right)\frac{\pi }
{2}}^{\phi = n\frac{\pi }
{2}} {\cos 2\phi \int_0^h {\int_0^h {\frac{1}
{{\sqrt {\left( {\zeta - z} \right)^2 + 4a^2 \cos ^2 \phi } }}} d\zeta dz} d\phi } \cr
& = - \frac{2}
{{\pi h}}\int_0^{\frac{\pi }
{2}} {\cos 2\phi \int_0^h {\int_{ - z}^{h - z} {\frac{1}
{{\sqrt {v^2 + 4a^2 \cos ^2 \phi } }}dv} dz} d\phi } \cr}
\end{align*}
\begin{align*}
\eqalign{
& fa = \frac{1}
{{\sqrt {v^2 + 4a^2 \cos ^2 \phi } }} \cr
& \int_0^h {\int_{ - z}^{h - z} {fa\;dv} dz} = \int_{}^h {\int_{}^{h - z} {fa\;dv} dz} - \int_{}^h {\int_{}^{ - z} {fa\;dv} dz} - \int_{}^0 {\int_{}^{h - z} {fa\;dv} dz} + \int_{}^0 {\int_{}^{ - z} {fa\;dv} dz} \cr
& = - \int_{}^0 {\int {fa\;dv^2 } } + \int_{}^{ - h} {\int {fa\;dv^2 } } + \int_{}^h {\int {fa\;dv^2 } } - \int_{}^0 {\int {fa\;dv^2 } } \cr
& = \int_{}^h {\int {fa\;dv^2 } } + \int_{}^{ - h} {\int {fa\;dv^2 } } - 2\int_{}^0 {\int {fa\;dv^2 } } \cr}
\end{align*}
\begin{align*}
\eqalign{
K & = - \frac{2}
{{\pi h}}\int_0^{\frac{\pi }
{2}} {\cos 2\phi \int_0^h {\int_{ - z}^{h - z} {fa\;dv} dz} d\phi } \cr
& = - \frac{2}
{{\pi h}}\int_0^{\frac{\pi }
{2}} {\cos 2\phi \left( {\int_{}^h {\int {fa\;dv^2 } } + \int_{}^{ - h} {\int {fa\;dv^2 } } - 2\int_{}^0 {\int {fa\;dv^2 } } } \right)d\phi } \cr
& = - \frac{2}
{{\pi h}}\int_0^{\frac{\pi }
{2}} {\cos 2\phi \left( {\int_{}^h {\int {\frac{1}
{{\sqrt {v^2 + 4a^2 \cos ^2 \phi } }}dv^2 } } + \int_{}^{ - h} {\int {\frac{1}
{{\sqrt {v^2 + 4a^2 \cos ^2 \phi } }}dv^2 } } - 2\int_{}^0 {\int {\frac{1}
{{\sqrt {v^2 + 4a^2 \cos ^2 \phi } }}dv^2 } } } \right)d\phi } \cr}
\end{align*}
\begin{align*}
\eqalign{
& Fa\left( {t,b} \right) = \int_{}^t {\int {\frac{1}
{{\sqrt {x^2 + b^2 } }}dx^2 } } = \int_{}^t {\ln \left( {x + \sqrt {x^2 + b^2 } } \right)dx} = t\ln \left( {t + \sqrt {t^2 + b^2 } } \right) - \sqrt {t^2 + b^2 } \cr
& Fb\left( t \right) = - \int_0^{\frac{\pi }
{2}} {\cos 2\phi \;Fa\left( {t,2a\cos \phi } \right)d\phi } \cr}
\end{align*}
\begin{align*}
\eqalign{
K & = - \frac{2}
{{\pi h}}\int_0^{\frac{\pi }
{2}} {\cos 2\phi \left\{ {Fa\left( {h,2a\cos \phi } \right) + Fa\left( { - h,2a\cos \phi } \right) - 2Fa\left( {0,2a\cos \phi } \right)} \right\}d\phi } \cr
& = \frac{2}
{{\pi h}}\left\{ {Fb\left( h \right) + Fb\left( { - h} \right) + 2Fb\left( 0 \right)} \right\} \cr}
\end{align*}
\begin{align*}
\eqalign{
Fb\left( x \right) & = - \int_0^{\frac{\pi }
{2}} {\cos 2\phi \;Fa\left( {x,2a\cos \phi } \right)d\phi } \cr
& = - \int_0^{\frac{\pi }
{2}} {\cos 2\phi \;\left\{ {x\ln \left( {x + \sqrt {x^2 + 4a^2 \cos ^2 \phi } } \right) - \sqrt {x^2 + 4a^2 \cos ^2 \phi } } \right\}d\phi } \cr
& = - \left[ {\sin \phi \cos \phi Fa\left( {x,2a\cos \phi } \right)} \right]_0^{\frac{\pi }
{2}} + \int_0^{\frac{\pi }
{2}} {\left( {\sin \phi \cos \phi } \right)\tan \phi \left( {\sqrt {x^2 + 4a^2 \cos ^2 \phi } - x} \right)d\phi } \cr
& = \int_0^{\frac{\pi }
{2}} {\sin ^2 \phi \left( {\sqrt {x^2 + 4a^2 \cos ^2 \phi } - x} \right)d\phi } \cr}
\end{align*}
$$
Fb\left( x \right) + Fb\left( { - x} \right) = 2\int_0^{\frac{\pi }
{2}} {\sin ^2 \phi \sqrt {x^2 + 4a^2 \cos ^2 \phi } d\phi }
$$
$$
Fb\left( 0 \right) = - \int_0^{\frac{\pi }
{2}} {\sin ^2 \phi \left( {2a\cos \phi } \right)d\phi } = - \frac{{2a}}
{3}
$$
\begin{align*}
\eqalign{
& \sqrt {h^2 + 4a^2 \cos ^2 \phi } = \sqrt {h^2 + 4a^2 - 4a^2 \sin ^2 \phi } \cr
& = \sqrt {h^2 + 4a^2 } \sqrt {1 - \frac{{4a^2 }}
{{h^2 + 4a^2 }}\sin ^2 \phi } = 2ak^{ - 1} \sqrt {1 - k^2 \sin ^2 \phi } \cr
& k = \frac{{2a}}
{{\sqrt {h^2 + 4a^2 } }} = \sqrt {1 + \left( {\frac{h}
{{2a}}} \right)^2 } ^{ - 1} = \cos{\left( \arctan{\frac{2a}{{h}}} \right)} \cr
& 1 + \left( {\frac{h}
{{2a}}} \right)^2 = k^{ - 2} \cr
& \frac{h}
{{2a}} = \sqrt {k^{ - 2} - 1} = \frac{{\sqrt {1 - k^2 } }}
{k} \cr}
\end{align*}
\begin{align*}
\eqalign{
K & = \frac{2}
{{\pi h}}\left\{ {Fb\left( h \right) + Fb\left( { - h} \right) + 2Fb\left( 0 \right)} \right\} \cr
& = \frac{2}
{{\pi h}}\left( {2\int_0^{\frac{\pi }
{2}} {\sin ^2 \phi \sqrt {x^2 + 4a^2 \cos ^2 \phi } d\phi } - \frac{{4a}}
{3}} \right) \cr
& = \frac{2}
{{\pi h}}\left( {4ak^{ - 1} \int_0^{\frac{\pi }
{2}} {\sin ^2 \phi \sqrt {1 - k^2 \sin ^2 \phi } d\phi } - \frac{{4a}}
{3}} \right) \cr
& = \frac{{8a}}
{{3\pi h}}\left( {3k^{ - 1} \int_0^{\frac{\pi }
{2}} {\sin ^2 \phi \sqrt {1 - k^2 \sin ^2 \phi } d\phi } - 1} \right) \cr
& = \frac{{4k}}
{{3\pi \sqrt {1 - k^2 } }}\left( {3k^{ - 1} \int_0^{\frac{\pi }
{2}} {\sin ^2 \phi \sqrt {1 - k^2 \sin ^2 \phi } d\phi } - 1} \right) \cr
& = \frac{4}
{{3\pi \sqrt {1 - k^2 } }}\left( {3\int_0^{\frac{\pi }
{2}} {\sin ^2 \phi \sqrt {1 - k^2 \sin ^2 \phi } d\phi } - k} \right) \cr}
\end{align*}
\begin{align*}
\eqalign{
& p = \sqrt {1 - k^2 \sin ^2 \phi } \cr
& k^2 \sin ^2 \phi = 1 - p^2 ,\;\sin ^2 \phi = \frac{{1 - p^2 }}
{{k^2 }} = k^{ - 2} - k^{ - 2} p^2 \cr
& \frac{d}
{{d\phi }}p = - k^2 p^{ - 1} \sin \phi \cos \phi \cr}
\end{align*}
\begin{align*}
\eqalign{
\frac{d}
{{d\phi }}p\sin \phi \cos \phi & = \left( { - k^2 p^{ - 1} \sin \phi \cos \phi } \right)\sin \phi \cos \phi + p\left( {1 - 2\sin ^2 \phi } \right) \cr
& = \left( {1 - 2\sin ^2 \phi } \right)p - p^{ - 1} k^2 \sin ^2 \phi \cos ^2 \phi \cr
& = \left( {1 - 2\sin ^2 \phi } \right)p - \left( {1 - p^2 } \right)\left( {1 - \sin ^2 \phi } \right)p^{ - 1} \cr
& = \left( {1 - 2\sin ^2 \phi } \right)p - \left( {p^{ - 1} - p} \right)\left( {1 - \sin ^2 \phi } \right) \cr
& = \left( {1 - 2\sin ^2 \phi } \right)p - \left( {1 - \sin ^2 \phi } \right)p^{ - 1} + \left( {1 - \sin ^2 \phi } \right)p \cr
& = \left( {2 - 3\sin ^2 \phi } \right)p - \left( {1 - k^{ - 2} + k^{ - 2} p^2 } \right)p^{ - 1} \cr
& = 2p - 3p\sin ^2 \phi - \left( {1 - k^{ - 2} } \right)p^{ - 1} - k^{ - 2} p \cr}
\end{align*}
\begin{align*}
\eqalign{
& 3p\sin ^2 \phi = \left( {k^{ - 2} - 1} \right)p^{ - 1} - \left( {k^{ - 2} - 2} \right)p - \frac{d}
{{d\phi }}p\sin \phi \cos \phi \cr
& 3\int_0^{\frac{\pi }
{2}} {\sin ^2 \phi \sqrt {1 - k^2 \sin ^2 \phi } d\phi } = \left( {k^{ - 2} - 1} \right)K\left( k \right) - \left( {k^{ - 2} - 2} \right)E\left( k \right) \cr}
\end{align*}
\begin{align*}
\eqalign{
K & = \frac{4}
{{3\pi \sqrt {1 - k^2 } }}\left( {3\int_0^{\frac{\pi }
{2}} {\sin ^2 \phi \sqrt {1 - k^2 \sin ^2 \phi } d\phi } - k} \right) \cr
& = \frac{4}
{{3\pi \sqrt {1 - k^2 } }}\left\{ {\left( {k^{ - 2} - 1} \right)K\left( k \right) - \left( {k^{ - 2} - 2} \right)E\left( k \right) - k} \right\} \cr
& = \frac{4}
{{3\pi \sqrt {1 - k^2 } }}\left\{ {\left( {\frac{1}
{{k^2 }} - 1} \right)K\left( k \right) - \left( {\frac{1}
{{k^2 }} - 2} \right)E\left( k \right) - k} \right\} \cr}
\end{align*}
ιょ ゃ ぃ b