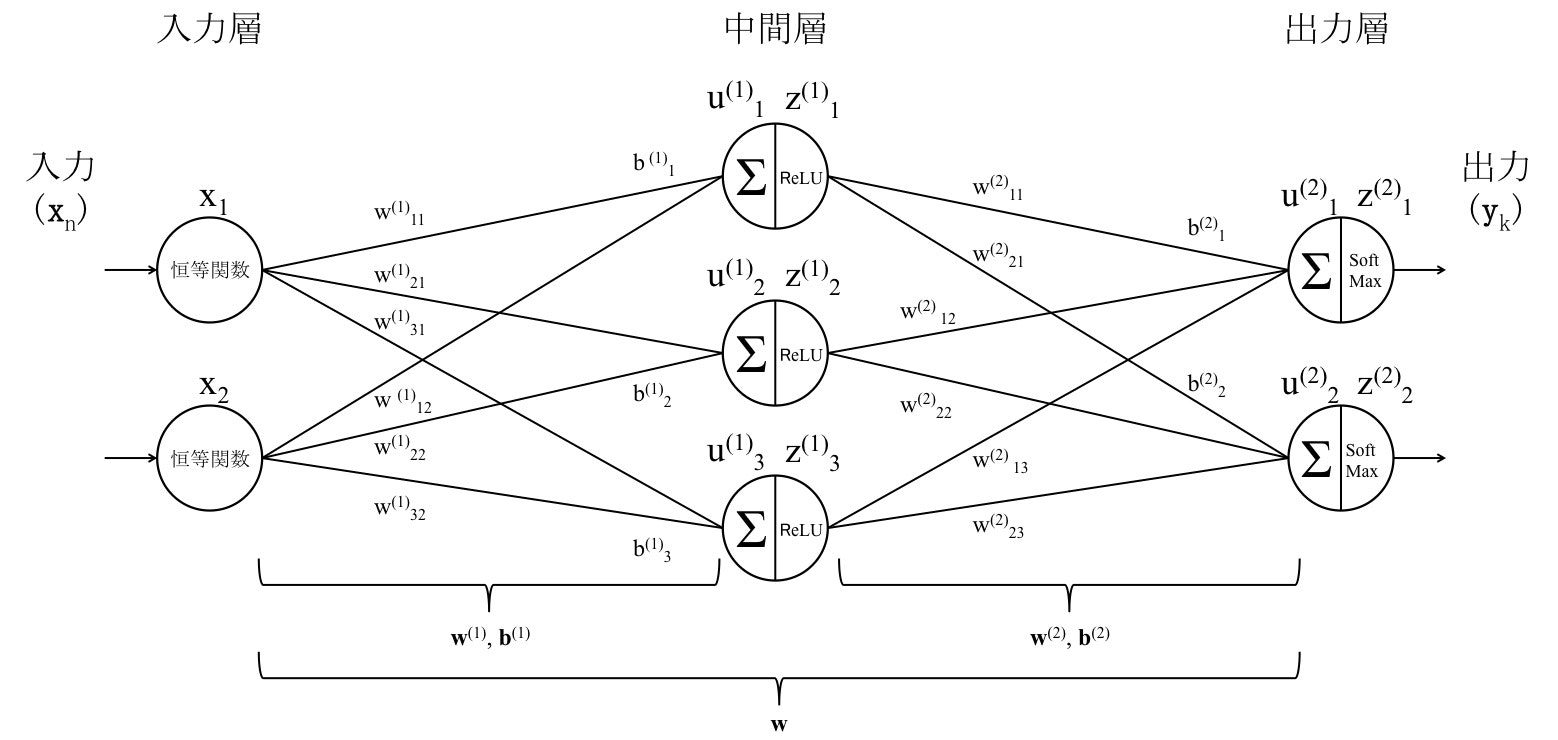
順伝播ニューラルネットワークは、入力層から出力層にかけて処理を行うニューラルネットワークモデルです。
ニューラルネットワークは、Python等のプログラム言語を使えば簡単に実装できます。
ですが、ここではプログラムの中身を理解するために、敢えてプログラムを使わずに(と言いつつ、検算でPythonを使いますが)順伝播ニューラルネットワークの出力値を計算してみます。
1.順伝播ニューラルネットワーク
まずは基本的な順伝播ニューラルネットワークモデル(入力層-中間層-出力層モデル)を考えます。
2.順伝播ニューラルネットワークモデルの出力値を計算で求めてみる
2.1.各層の計算
- 入力層の計算
\boldsymbol{x}
- 中間層の計算
\boldsymbol{u}^{(1)}=\boldsymbol{w}^{(1)}\cdot\boldsymbol{x}+ \boldsymbol{b}_1 \\
\boldsymbol{z}^{(1)} = f(\boldsymbol{u}^{(1)}) \\
- 出力層の計算
\boldsymbol{u}^{(2)}=\boldsymbol{z}^{(1)}\cdot\boldsymbol{w}^{(2)} + \boldsymbol{b}_2 \\
\boldsymbol{z}^{(2)} = f(\boldsymbol{u}^{(2)})
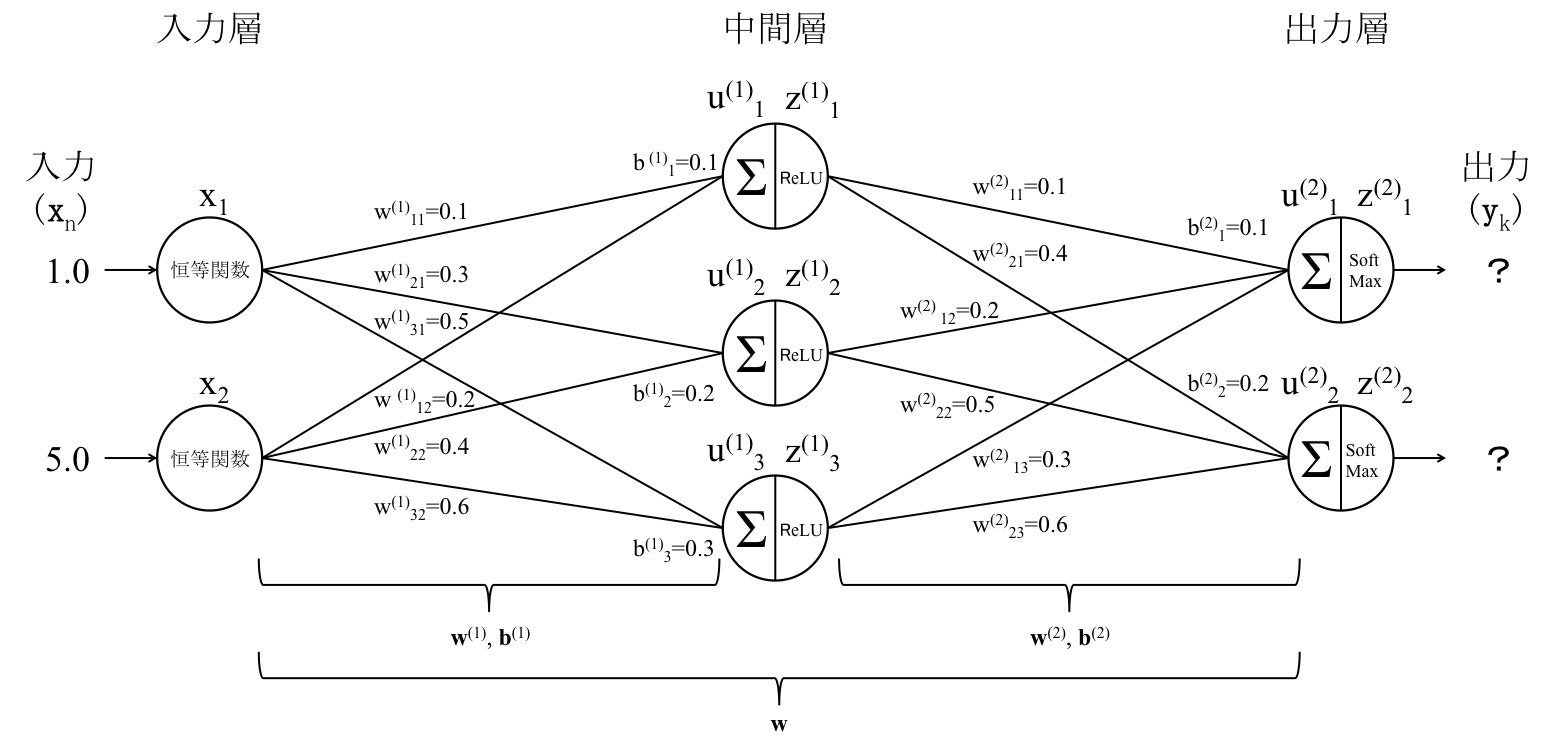
2.2.初期条件の設定
インプット$\bf{x}$、重み$\bf{w}$、バイアス$\bf{b}$をそれぞれ下記の値とします。
\boldsymbol{x}=
\begin{pmatrix}
x_1\\
x_2
\end{pmatrix}
=
\begin{pmatrix}
1.0\\
5.0
\end{pmatrix}
\boldsymbol{w}^{(1)}=
\begin{pmatrix}
w_{11}^{(1)} & w_{12}^{(1)} \\
w_{21}^{(1)} & w_{22}^{(1)} \\
w_{31}^{(1)} & w_{32}^{(1)}
\end{pmatrix}
=
\begin{pmatrix}
0.1 & 0.2 \\
0.3 & 0.4 \\
0.5 & 0.6
\end{pmatrix}
\boldsymbol{b}^{(1)}=
\begin{pmatrix}
b_1^{(1)} \\
b_2^{(1)} \\
b_3^{(1)}
\end{pmatrix}
=
\begin{pmatrix}
0.1 \\
0.2 \\
0.3
\end{pmatrix}
\boldsymbol{w}^{(2)}=
\begin{pmatrix}
w_{11}^{(2)} & w_{12}^{(2)} & w_{13}^{(2)} \\
w_{21}^{(2)} & w_{22}^{(2)} & w_{23}^{(2)}
\end{pmatrix}
=
\begin{pmatrix}
0.1 & 0.2 & 0.3 \\
0.4 & 0.5 & 0.6
\end{pmatrix}
\boldsymbol{b}^{(2)}=
\begin{pmatrix}
b_1^{(2)} \\
b_2^{(2)}
\end{pmatrix}
=
\begin{pmatrix}
0.1 \\
0.2
\end{pmatrix}
2.3.順伝播型ニューラルネットワークの出力計算
中間層入力は、
\begin{equation}
\begin{split}
\boldsymbol{u}^{(1)} &= \boldsymbol{w}^{(1)}\cdot\boldsymbol{x}+ \boldsymbol{b}_1 \\
&=
\begin{pmatrix}
w_{11}^1 & w_{12}^1\\
w_{21}^1 & w_{22}^1\\
w_{31}^1 & w_{32}^1
\end{pmatrix}
\begin{pmatrix}
x_1\\
x_2
\end{pmatrix}
+
\begin{pmatrix}
b_{11} \\
b_{12} \\
b_{13}
\end{pmatrix} \\
&=
\begin{pmatrix}
0.1 & 0.2\\
0.3 & 0.4\\
0.5 & 0.6
\end{pmatrix}
\begin{pmatrix}
1.0\\
5.0
\end{pmatrix}
+
\begin{pmatrix}
0.1 \\
0.2 \\
0.3
\end{pmatrix} \\
&=
\begin{pmatrix}
1.2\\
2.5\\
3.8
\end{pmatrix}
\end{split}
\end{equation}
となります。
活性化関数はReLU関数とします。
ReLU関数は下記の式で与えられます。
f(x) = ReLU(x) = \left\{
\begin{array}{l}
x & (x > 0) \\
0 & (otherwise)
\end{array}
\right.
よって中間層出力は、
\boldsymbol{z}^{(1)}
=
\begin{pmatrix}
z_1^{(1)} \\
z_2^{(1)} \\
z_3^{(1)}
\end{pmatrix}
=
\begin{pmatrix}
ReLU(u_1^{(1)}) \\
ReLU(u_2^{(1)}) \\
ReLU(u_3^{(1)})
\end{pmatrix}
=
\begin{pmatrix}
ReLU(1.2) \\
ReLU(2.5) \\
ReLU(3.8)
\end{pmatrix}
=
\begin{pmatrix}
1.2\\
2.5\\
3.8
\end{pmatrix}
となります。
同様に、出力層入力は、
\begin{equation}
\begin{split}
\boldsymbol{u}^{(2)} &= \boldsymbol{w}^{(2)}\cdot\boldsymbol{z}^{(1)}+ \boldsymbol{b}_2 \\
&=
\begin{pmatrix}
w_{11}^{(2)} & w_{12}^{(2)} & w_{13}^{(2)}\\
w_{21}^{(2)} & w_{22}^{(2)} & w_{23}^{(2)}
\end{pmatrix}
\begin{pmatrix}
z_1^{(1)}\\
z_2^{(1)}\\
z_3^{(1)}
\end{pmatrix}
+
\begin{pmatrix}
b_{21} \\
b_{22}
\end{pmatrix} \\
&=
\begin{pmatrix}
0.1 & 0.2 & 0.3 \\
0.4 & 0.5 & 0.6
\end{pmatrix}
\begin{pmatrix}
1.2\\
2.5\\
3.8
\end{pmatrix}
+
\begin{pmatrix}
0.1 \\
0.2
\end{pmatrix} \\
&=
\begin{pmatrix}
1.86\\
4.21
\end{pmatrix}
\end{split}
\end{equation}
となります。
今回は多クラス分類問題を想定しているため、出力層の活性化関数にはSoftmax関数を用います。
Softmax関数は下記で与えられます。
f(x) = Softmax(x) = \frac{exp(x_k)}{\sum_{i=1}^n exp(x_i)}
よって最終出力は、
\boldsymbol{z}^{(2)}
=
\begin{pmatrix}
z_1^{(1)} \\
z_2^{(2)}
\end{pmatrix}
=
\begin{pmatrix}
Softmax(u_1^{(2)}) \\
Softmax(u_2^{(2)})
\end{pmatrix}
=
\begin{pmatrix}
Softmax(1.86) \\
Softmax(4.21)
\end{pmatrix}
=
\begin{pmatrix}
\frac{exp(1.86)}{exp(1.86) + exp(4.21)} \\
\frac{exp(4.21)}{exp(1.86) + exp(4.21)}
\end{pmatrix}
=
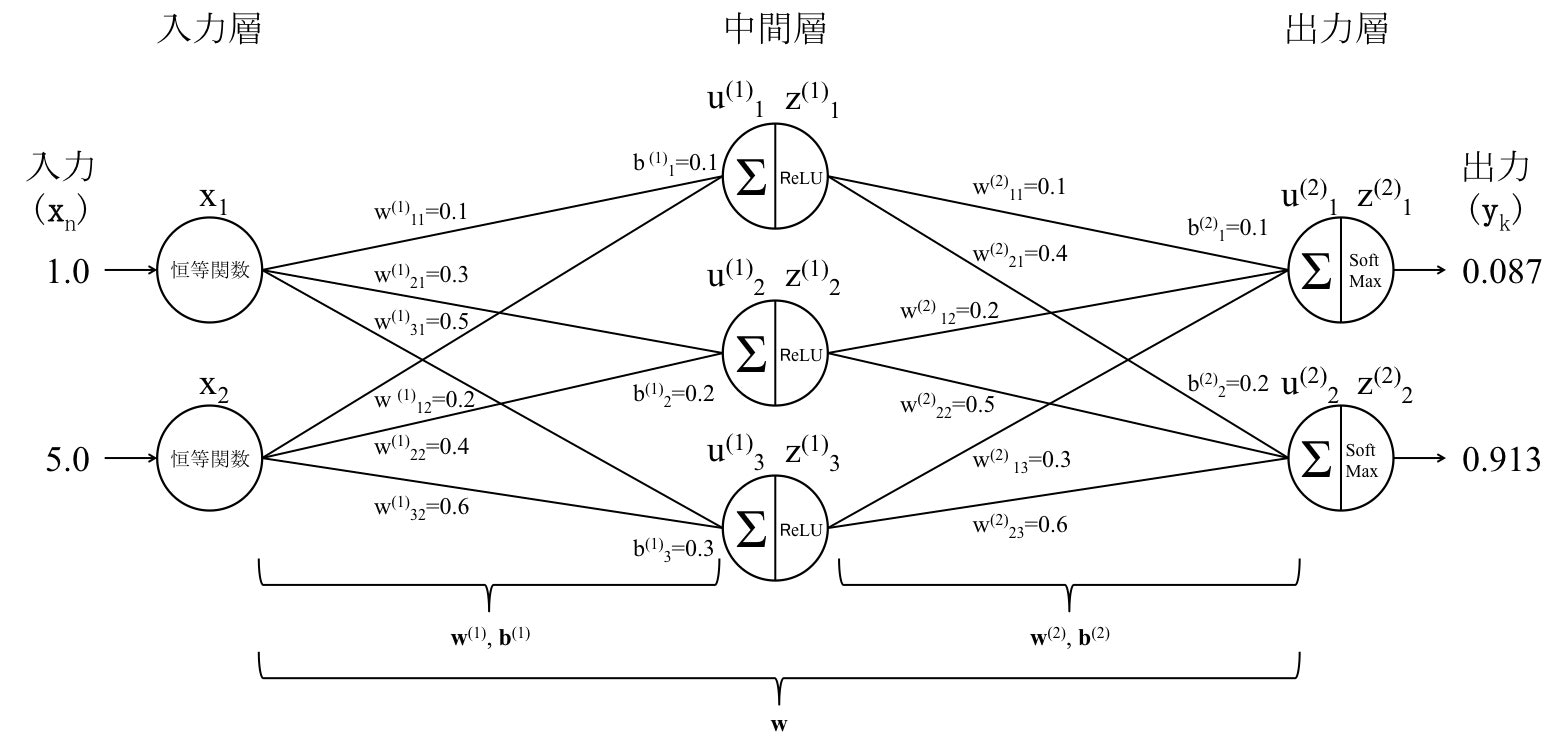
\begin{pmatrix}
0.0870… \\
0.9129…
\end{pmatrix}
となります。
3.Pythonを用いて検算をする
実際にPythonに計算させて、手で解いた値が正しいかを検算します。
import numpy as np
import sys
# 順伝播型ネットワークの実行
def main():
args = sys.argv
x = np.array([[float(args[1]), float(args[2])]])
network = init_network()
y, z1 = forward(network, x)
print(y)
# ネートワークを作成
def init_network():
print("##### ネットワークの初期化 #####")
network = {}
network['W1'] = np.array([
[0.1, 0.3, 0.5],
[0.2, 0.4, 0.6]
])
network['W2'] = np.array([
[0.1, 0.4],
[0.2, 0.5],
[0.3, 0.6]
])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['b2'] = np.array([0.1, 0.2])
print_vec("重み1", network['W1'])
print_vec("重み2", network['W2'])
print_vec("バイアス1", network['b1'])
print_vec("バイアス2", network['b2'])
return network
# 順伝播
def forward(network, x):
print("##### 順伝播開始 #####")
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
u1 = np.dot(x, W1) + b1
z1 = relu(u1)
u2 = np.dot(z1, W2) + b2
y = softmax(u2)
print_vec("総入力1", u1)
print_vec("中間層出力1", z1)
print_vec("総入力2", u2)
print_vec("出力", y)
print("出力合計: " + str(np.sum(y)))
return y, z1
# 表示
def print_vec(text, vec):
print("*** " + text + " ***")
print(vec)
print("")
# 中間層の活性化関数
# ReLU関数
def relu(x):
return np.maximum(0, x)
# 出力層の活性化関数
# ソフトマックス関数
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
if __name__ == '__main__':
main()
このプログラムを実行してみます。
ターミナルを開いて下記コマンドで実行します。
$ python forward_network.py 1.0 5.0
出力結果は下記の通りとなり、結果が一致していることがわかります。
##### ネットワークの初期化 #####
*** 重み1 ***
[[0.1 0.3 0.5]
[0.2 0.4 0.6]]
*** 重み2 ***
[[0.1 0.4]
[0.2 0.5]
[0.3 0.6]]
*** バイアス1 ***
[0.1 0.2 0.3]
*** バイアス2 ***
[0.1 0.2]
##### 順伝播開始 #####
*** 総入力1 ***
[[1.2 2.5 3.8]]
*** 中間層出力1 ***
[[1.2 2.5 3.8]]
*** 総入力2 ***
[[1.86 4.21]]
*** 出力 ***
[[0.08706577 0.91293423]]
出力合計: 1.0
[[0.08706577 0.91293423]]
4.終わりに
次は、逆伝播を手で解いてみたいと思います。