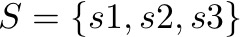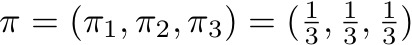CFTPについてのまとめとサンプルコード

CFTPとは

coupling from the past　の略。
無限の攪拌時間を要することなく
目的の分布に厳密に従うサンプリングを行うことができる。

詳しいことは以下のリンクを見るべし。

#リンク
CFTPの説明（日本語）
CFTPに関する書籍(日本語)「やさしいmcmc入門」
David Bruce Wilson氏の論文全て
CFTPに関する論文
RCFTPに関する論文
David Bruce Wilson氏のRCFTPを用いたコード

#サンプルコード
状態空間S

推移関数P

をもつマルコフ連鎖は明らかに次の定常分布を持つ

simple_cftp1.c

#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <iostream>
#include <math.h>
using namespace std;


const int STATE_NUM = 3 ;
//更新
int move(int state, int  &r){
    switch(state){
        case 0:
            if(r) return 0;
            else return 1;
            break;
            
        case STATE_NUM - 1:
            if(r) return state - 1;
            else return state;
            break;
            
        default:
            if(r) return state - 1;
            else return state + 1;
    }
}

int q(){
    //更新関数に食わせる確率変数は使い回す必要があるので保存しておく
    vector<int> r_list;
    
    int state1 = 0;
    int state2 = 1;
    int state3 = 2;

    int n = 0;
    while(state1 != state2 || state1 != state3){
        state1 = 0;
        state2 = 1;
        state3 = 2;
        int size = r_list.size();
        for(int i = 0; i < pow(2,n) - size ; i++){
            r_list.push_back(rand() % 2);
        }
        n++;
        
        
        for(int i = r_list.size() - 1; i >= 0; i--){
            
            state1 = move(state1, r_list[i]);
            state2 = move(state2, r_list[i]);
            state3 = move(state3, r_list[i]);

            
        }
    }
    return state1;
    

}

void sample(int n){
    int samples[STATE_NUM] = {0};
    
    for(int i = 0; i < n; i++){
        samples[q()]++;
    }
    for(int i = 0; i < STATE_NUM; i++){
        cout << (double)samples[i] / n << "\n";
    }
    
}

int main(){
    srand((unsigned)time(NULL));
    sample(200);
    
}

結果

0.325
0.37
0.305

既知の定常分布と結果を比較すると
正しくサンプリングされていることが分かる

#単調CFTP、挟み撃ち法のサンプルコード
状態空間と推移行列は上記のサンプルと同じ。

このマルコフ連鎖は単調なので挟み撃ち法が使える。
つまり、一番上のs1を初期状態とするstate1と一番下のs3を初期状態とするstate2を用意し
state1とstate2が一致しことを終了条件にすれば良い。

sandwich_cftp.c

#include <stdio.h>
#include <stdlib.h>
#include <vector>
#include <iostream>
#include <math.h>
using namespace std;


const int STATE_NUM = 3 ;
//更新
int move(int state, int  &r){
    switch(state){
        case 0:
            if(r) return 0;
            else return 1;
            break;
            
        case STATE_NUM - 1:
            if(r) return state - 1;
            else return state;
            break;
            
        default:
            if(r) return state - 1;
            else return state + 1;
    }
}

int q(){
    //更新関数に食わせる確率変数は使い回す必要があるので保存しておく
    vector<int> r_list;
    
    int state1 = -1;
    int state2 = -2;

    int n = 0;
    while(state1 != state2){
        state1 = 0;
        state2 = STATE_NUM - 1;
        int size = r_list.size();
        for(int i = 0; i < pow(2,n) - size ; i++){
            r_list.push_back(rand() % 2);
        }
        n++;
        
        
        for(int i = r_list.size() - 1; i >= 0; i--){
            
            state1 = move(state1, r_list[i]);
            state2 = move(state2, r_list[i]);

            
        }
    }
    return state1;
    

}

void sample(int n){
    int samples[STATE_NUM] = {0};
    
    for(int i = 0; i < n; i++){
        samples[q()]++;
    }
    for(int i = 0; i < STATE_NUM; i++){
        cout << (double)samples[i] / n << "\n";
    }
    
}

int main(){
    srand((unsigned)time(NULL));
    sample(200);
    
}

結果

0.344734
0.326233
0.329033

既知の定常分布と結果を比較すると
正しくサンプリングされていることが分かる