日常の小さな違和感
ある日、トイレに行って気づきがありました。
最近、めんどくさかったので、空になったトイレットペーパーの芯をゴミ箱に入れず、自室の適当な本棚の上に置いていました。それを何日か続けているうちに、だんだんとトイレットペーパーの芯の数が増えていきました。そこで、なんか妙にハイペースでトイレットペーパーが無くなるな。と思うようになりました。
それ自身は単純に自分がトイレットペーパー使いすぎなのかな?と思っていたのですが、それ以上に別の気づきを感じました。
新品の時にはトイレットペーパーを使うと減り具合が少ないが、半分ぐらいになると妙にトイレットペーパーの減り具合が多くなる
ような気がしてきました。
よくよく理性的に考えると当たり前で、新品のトイレットペーパーは紙が多い分、半径が大きくなるので、一周分の紙の量が多い。しかし、一方で巻かれている量が半分ぐらいになると、半径が小さくなっているので、一周分の紙の量が少ない。そうすると、定量でトイレットペーパーを使っていると、半分ぐらい使ったトイレットペーパーの方が速く減るように感じる。というのは、直感的には正しいです。
では、実際どれくらい早い速度でなくなっているのでしょうか。
数理モデルで戦う
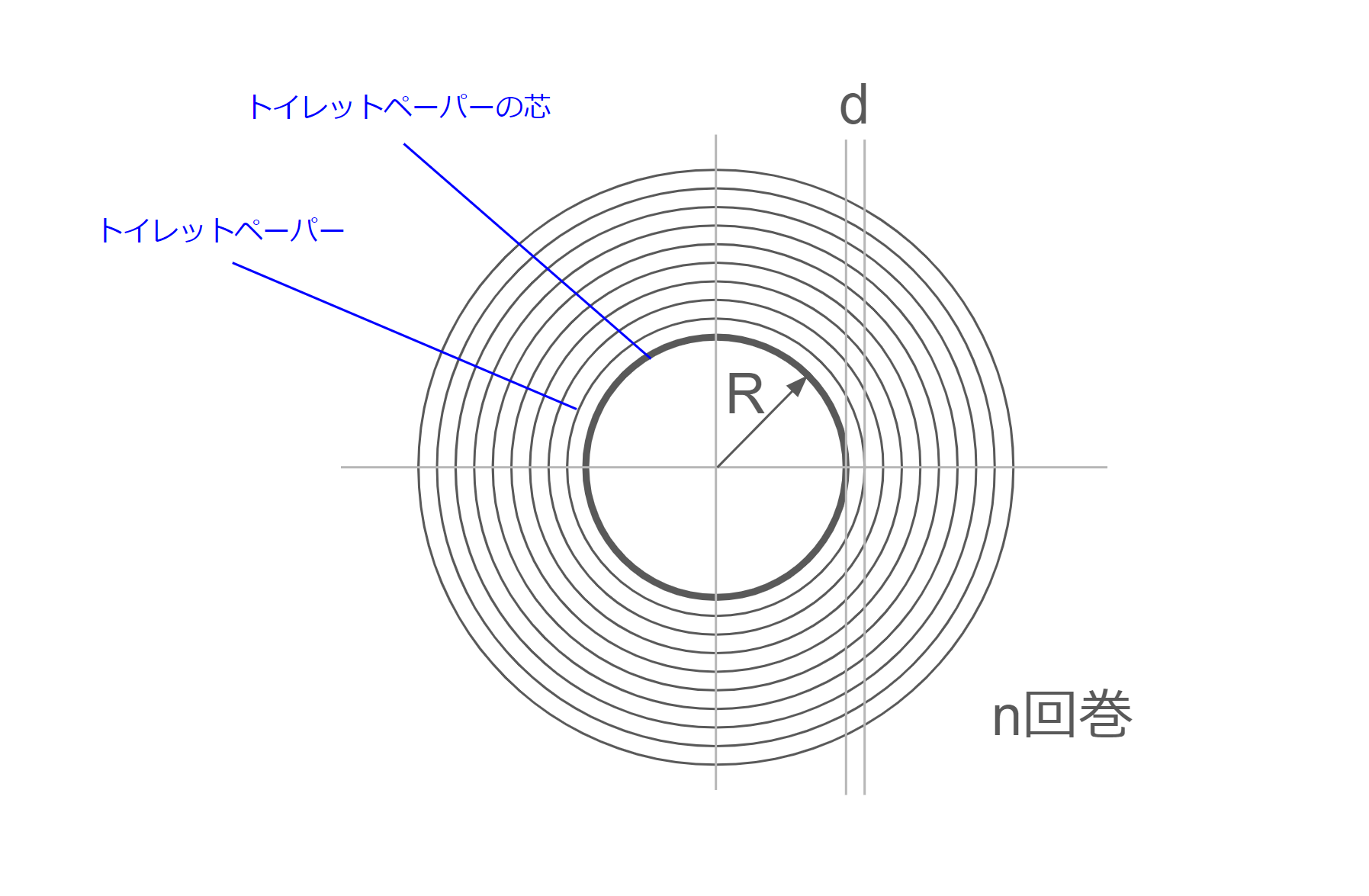
以下のような条件で数理モデルを考えてみます。今回考えているのは、シンプルなモデルで、芯に対し紙が同心円状に巻いていると想定して計算します。
\begin{align}
R:トイレットペーパーの芯の半径 \\
d:トイレットペーパーの厚さ \\
n:トイレットペーパーの巻数 \\
\end{align}
この時、n回紙を巻いた時のトイレットペーパーロールの半径r_{n}は、
r_{n} = R + d \left(n - 1\right)
と表されます。またこのn回目、巻く際に必要なトイレットペーパーの長さl_{n}は、直径×円周率のため、
l_{n} = 2 \pi r_{n}
と表されます。この時、n回トイレットペーパーを巻くのに必要なトイレットペーパーの長さLは、
\begin{align}
L &= \sum_{i=1}^{n} l_{i} \\
&= \sum_{i=1}^{n} 2 \pi r_{n} \\
&= \sum_{i=1}^{n} 2 \pi \lbrace R + d \left(n - 1\right) \rbrace \\
&= \pi n \left(2 R + d n - d\right)
\end{align}
等差数列の和の公式からLが求めることが出来ます。このLをnについて解きます。
\pi d n^{2} + n \left(2 \pi R - \pi d\right)-L = 0
上記のLからnに関する二次方程式を得ます。これを解くと、
n = - \frac{R}{d} + \frac{1}{2} \pm \frac{\sqrt{4 \pi R^{2} - 4 \pi R d + \pi d^{2}
+ 4 d L}}{2 \sqrt{\pi} d}
を得ます。ここでn>0より、
n = - \frac{R}{d} + \frac{1}{2} + \frac{\sqrt{4 \pi R^{2} - 4 \pi R d + \pi d^{2}
+ 4 d L}}{2 \sqrt{\pi} d}
と分かります。上式をr_nへ代入し、rをLで表します。
r(L) = - \frac{d}{2} + \frac{\sqrt{4 \pi R^{2} - 4 \pi R d + \pi d^{2} + 4 d L}}{2 \sqrt{\pi}}
ここからトイレットペーパーの半径とトイレットペーパーの長さの関係が分かりました。
ここで、このサイトより、トイレットペーパーの芯の直径は38mm、紙の厚さを0.02mmとすると、
r(L) = \frac{18.99 \sqrt{5.54600256613539 \cdot 10^{-5} L + \pi}}{\sqrt{\pi}} - 0.01
となります。このグラフを描くと、
となります。このグラフからなんとなく、xが大きくなるほどグラフの変化率が小さくなるグラフであるだろう。ということが分かります。それはr(L)の式からも言えて、半径はおおむねsqrt(L)に比例すると捉えることが出来ます。
また、トイレットペーパーの長さを30mとしたとき、
\begin{align}
\pi n \left(2 R + d n - d\right) &= 30 * 1000 \\
\pi n \left(0.02 n + 37.98\right) &= 30 * 1000 \\
n &\simeq 224.81
\end{align}
概ねトイレットペーパーの巻き数は224であることが分かります。
ここで、変化率を緻密に見るためにr(L)のLに対する微分を計算します。
\frac{dr}{dL} = \frac{d}{\sqrt{\pi} \sqrt{4 \pi R^{2} - 4 \pi R d + \pi d^{2} + 4 d L}}
この式からもLが大きくなるにつれ、傾きがどんどん小さくなっていき、0に近づいていく(=グラフがだんだん寝てくる)ことが分かります。
また、以下のような等式を考えます。
R + d ( \tilde{n} - 1 ) = R + v d (n-1)
トイレットペーパー部の厚みがv倍の時のnを\tilde{n}とします。解を求めると、
\tilde{n} = nv - v + 1
となります。ここで、n回巻いた時の微分と、\tilde{n}回巻いた時の微分を比較します。
\begin{align}
\frac{\left.\frac{dr}{dL}\right|_{L=L(\tilde{n})}}{\left.\frac{dr}{dL}\right|_{L=L(n)}} &= \frac{\sqrt{4 \pi R^{2} - 4 \pi R d + \pi d^{2} + 4 \pi d n \left(2 R + d n -d\right)}}{\sqrt{4 \pi R^{2} - 4 \pi R d + \pi d^{2} + 4 \pi d \left(2 R + d \left(n v - v + 1\right) - d\right) \left(n v - v + 1\right)}} \\
&= \frac{2 R + 2 d n - d}{2 R + 2 d n v - 2 d v + d}
\end{align}
ここで、実際の値を計算するため、n=112、v=2として値を計算すると
\frac{\left.\frac{dr}{dL}\right|_{L=L(\tilde{n})}}{\left.\frac{dr}{dL}\right|_{L=L(n)}} \simeq 0.9
となります。これをかみ砕いて説明すると、トイレットペーパーが新品の時と、トイレットペーパーを半分使っている時では、新品の方が半径の減る速度が0.9倍速い(≒10%ほど遅い)。ということが分かります。
数学の厳密性を少し脇に置いて解釈すると、 トイレットペーパーを使い始めて、半分まで使うのに仮に4日間かかるとすると、半分からトイレットペーパーがなくなるまでは3.6日(3日と14時間と少し)になる。 ということです。一般家庭では1人1週間に1ロール使うらしいので、だいたいこんな感じです。
月曜日の朝に新品のトイレットペーパーを開けたら、金曜日の朝に半分になっていて、来週の月曜日の昼過ぎに無くなるイメージです。
なので、私がトイレットペーパーに抱いていた違和感は正しく、 トイレットペーパーが新品の時と、直径が半分の時では半分の時の方がトイレットペーパーは速く無くなっていました。そして、半分になると、新品の時より、約1割程度速い速度で無くなっていく。ということが分かりました。
Sympyによる解析
という今までの解析はPythonのsympyという記号計算を行うライブラリで解いていました。Lを求めるぐらいまでは手動でやっていて出来たのですが、それ以上になってくると√πなど、ちょっと手動で触るにはキツイ数式になってきたので、sympyに任せました。
from sympy import *
init_printing()
rr = 38 / 2
dr = 2e-2
lr = 30 * 1000
R,d,i,n,s,P,g,N,l = symbols("R d i n s P g N l",positive=True,real=True)
r_n = R + (n - 1) * d
l_n = 2 * pi * r_n
# 総和の式
sum_formula = summation(l_n, (n, 1, n)).simplify()
nr = solve(sum_formula.subs(R,rr).subs(d,dr)-lr,n)[0]
a = r_n.subs(n,solve(l-sum_formula,n)[1]).expand().simplify()
al = a.diff(l)
u,v = symbols("u v",positive=True,real=True)
u = solve(R+d*(u-1)-(R+v*d*(n-1)),u)[0]
p = (al.subs(l,sum_formula.subs(n,u))/al.subs(l,sum_formula)).expand().factor()
理解とは何か
このトイレットペーパーのネタは前々から疑問に思っており、趣味がてら立式して、数式をつぶしてみたりしていました。最初に書いたように、新品の時は径が大きく、減りが少ない。使い始めると径が小さくなり、減りが多くなる。という直感はありました。しかし、それをもう少し定量的に言いたいなぁ。という気持ちが出始めて、sympyでゴリゴリと解析をしていました。しかし、難産だった。
「理解できた」という言葉はどういう意味なのだろうか。
と思うことが多くあります。今回の議論で言えば、rやrの微分を求めた時点でほぼ答えは決まっていて、長さLが大きくなるほど、半径への影響は小さくなる。ということは言えていました。しかし、では、どれだけか?というところで、この"どれだけ"を言うのがとても難しかった。今回はrの微分に、巻き数nと\tilda{n}を代入し、その割合を調べることである程度、綺麗な数式に落とし込むことはできました。しかし、一次式/一次式という、どうも直感理解がしにくい数式になってしまいました。そのため、最終的には実際の値を代入することで数値表現とすることで、0.9倍という値が出て、ある程度理解が進みました。
ただ個人的には、この実際の値を入れるのは最終手段であり、もう少し記号操作でなんとかなったのではないか・・・と思っています。それは、自分が持っている数式のイメージが貧弱だから、直感理解できないのか、もしくはもっとよい変形があり、そちらの方だともっとわかりやすかったのだろうか・・・