技術書典11で本を出しました
REST APIを題材として、E2Eの自動テストの環境を構築するのを目的とした本です。
E2Eテストはテストの効果は高いですが、保守コストが高いと言われています。そして、その自動テストの構築には相応の学習コスト・構築コストが必要となります。
本書では、Go+gorilla/muxで構築したREST APIのDockerイメージを作成し、DockerComposeを用いてMySQLサーバーと連携させながら、GithubActionsでCIが動くまでを解説しています。
これにより、読者が保守性の高く、運用コストの低い、E2Eテスト環境を手に入れられることを目標とした一冊となっています。
売れ行きが気になる
今回、同人誌を作るのは初めてでした。そのため、どれくらい売れるのか?というのが分かりませんでした。そこで、
機械学習で自分の本の売り上げを予測しよう。
ということを思い立ちました。
そこで、作ったGoogleColabがこちらです。
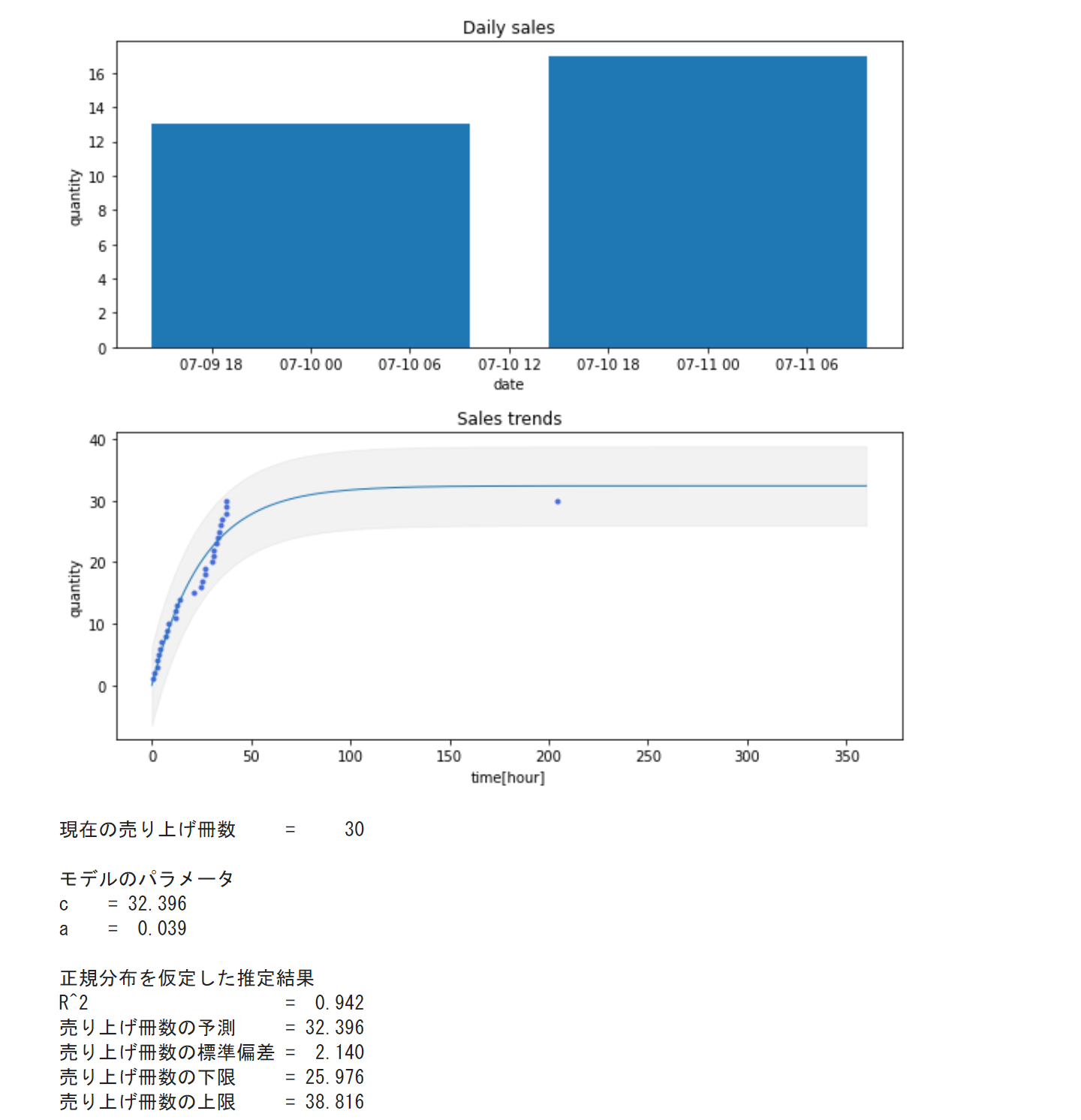
実際の動作結果がこちらです。(公開しているnotebookはデータを改変しています)
使い方は「ランタイム > すべてのセルを実行」から予測を実行することができます。
自分の売り上げデータで予測する
このnotebookは汎用的に作ってあるので、データを入力すると、自分の本の売り上げが予測できます。
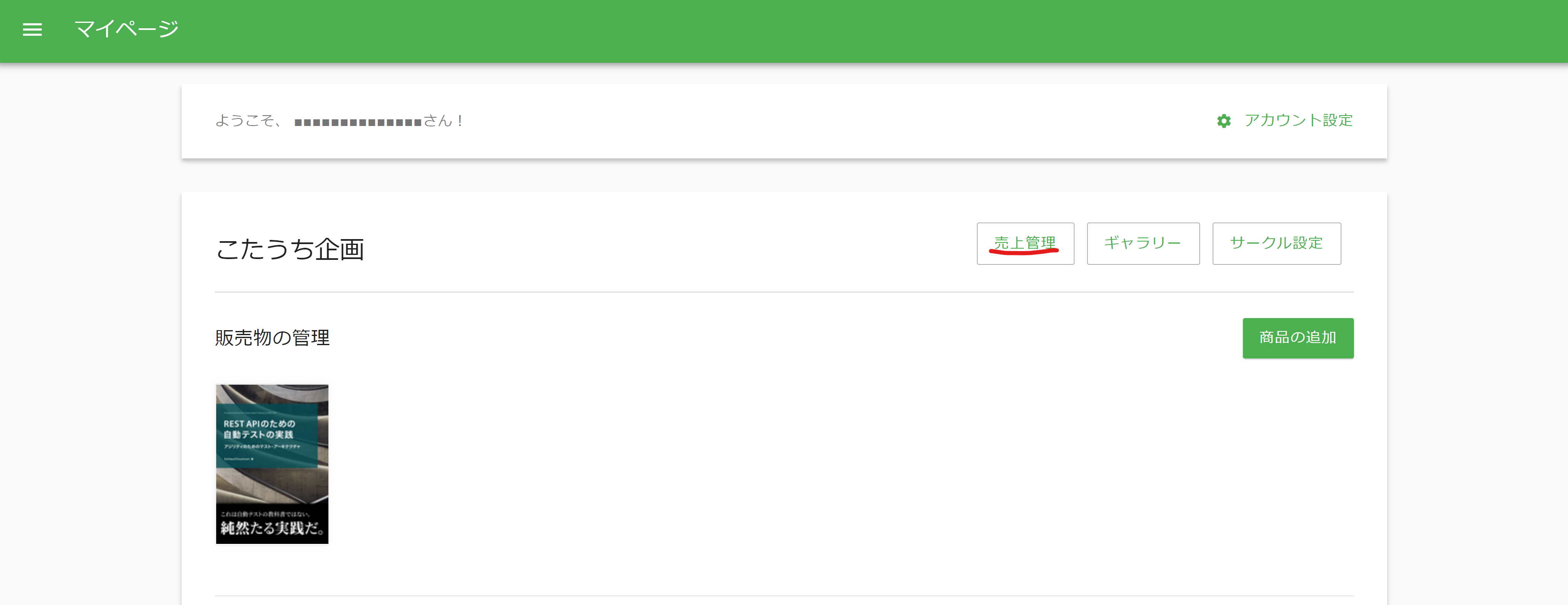
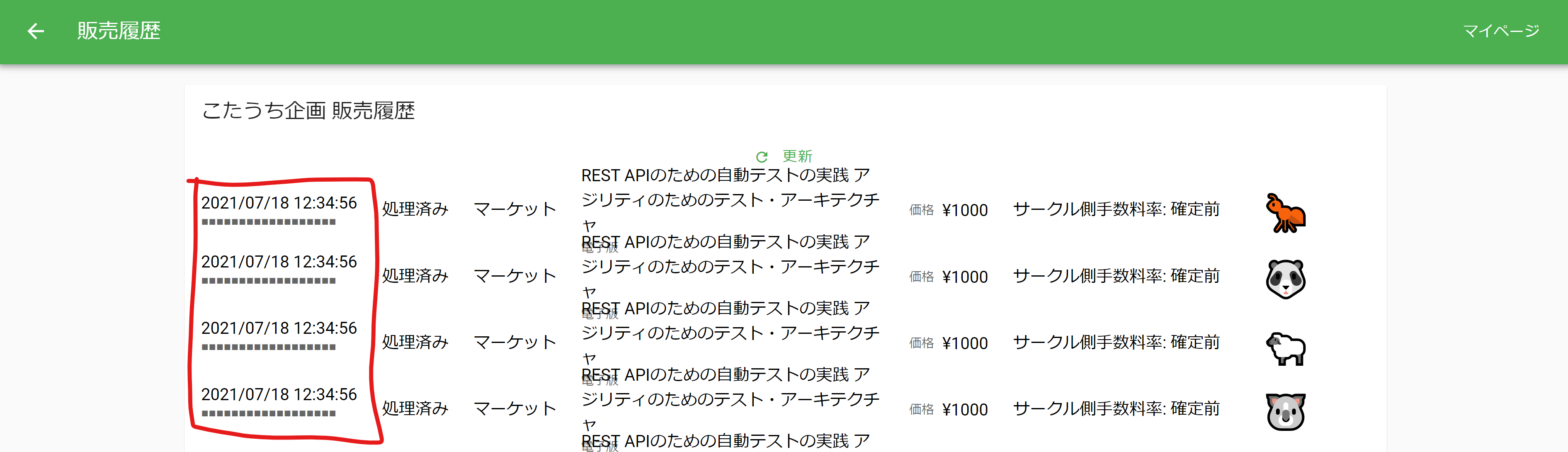
まず技術書展の「マイページ」にある「売上管理」をクリックします(執筆の都合上一部データを改変してます)。
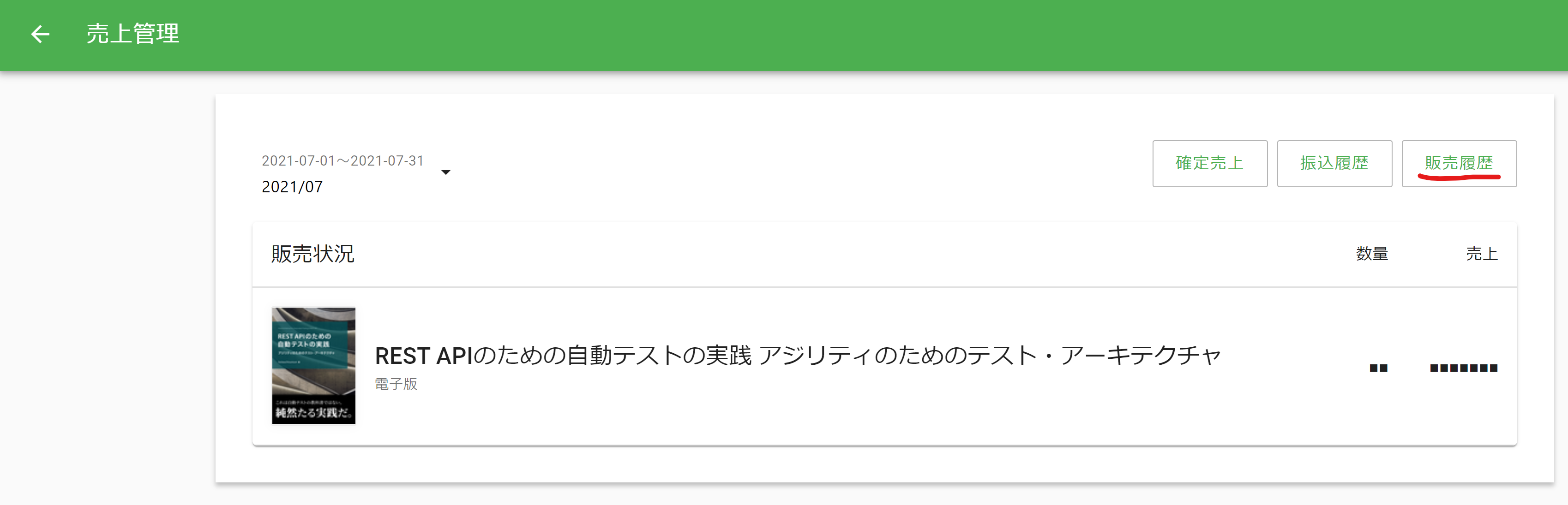
「売り上げ管理」のページから「販売履歴」をクリックします。
そうすると以下の様に売り上げ時刻が分かります。
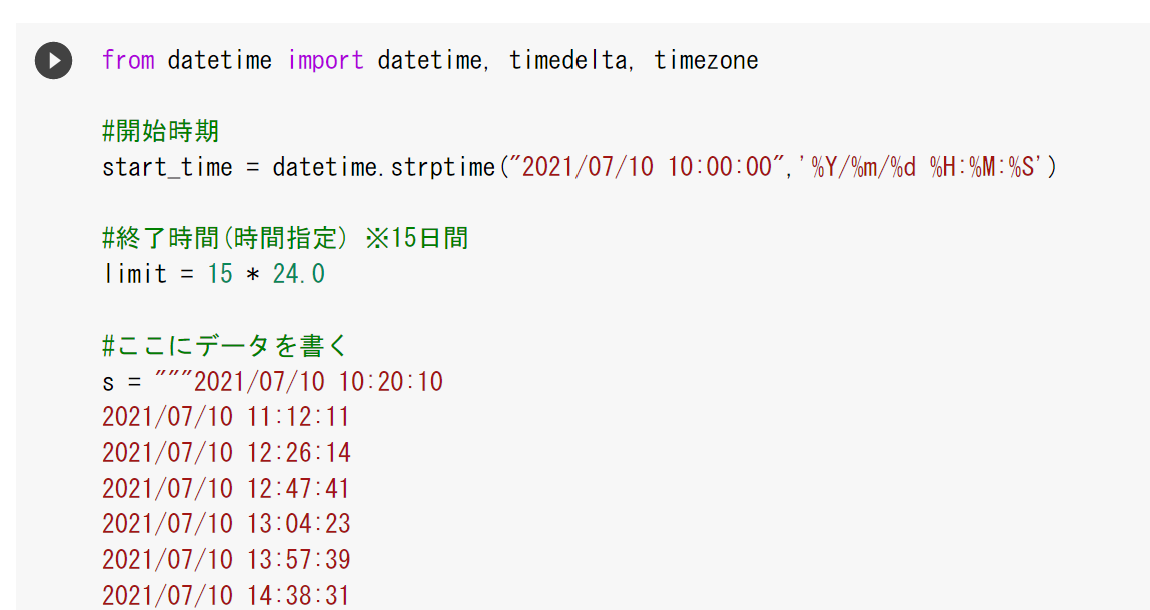
これらのデータを「#ここにデータを書く」と書かれている部分と置き換えます。そのあと、実行することで自分のデータで予測することができます。
また、割と一般的なつくりをしているので、「開始時刻」「終了時間」をいじってもらうことで、他の用途にも応用出来ます。
数理モデルの探求
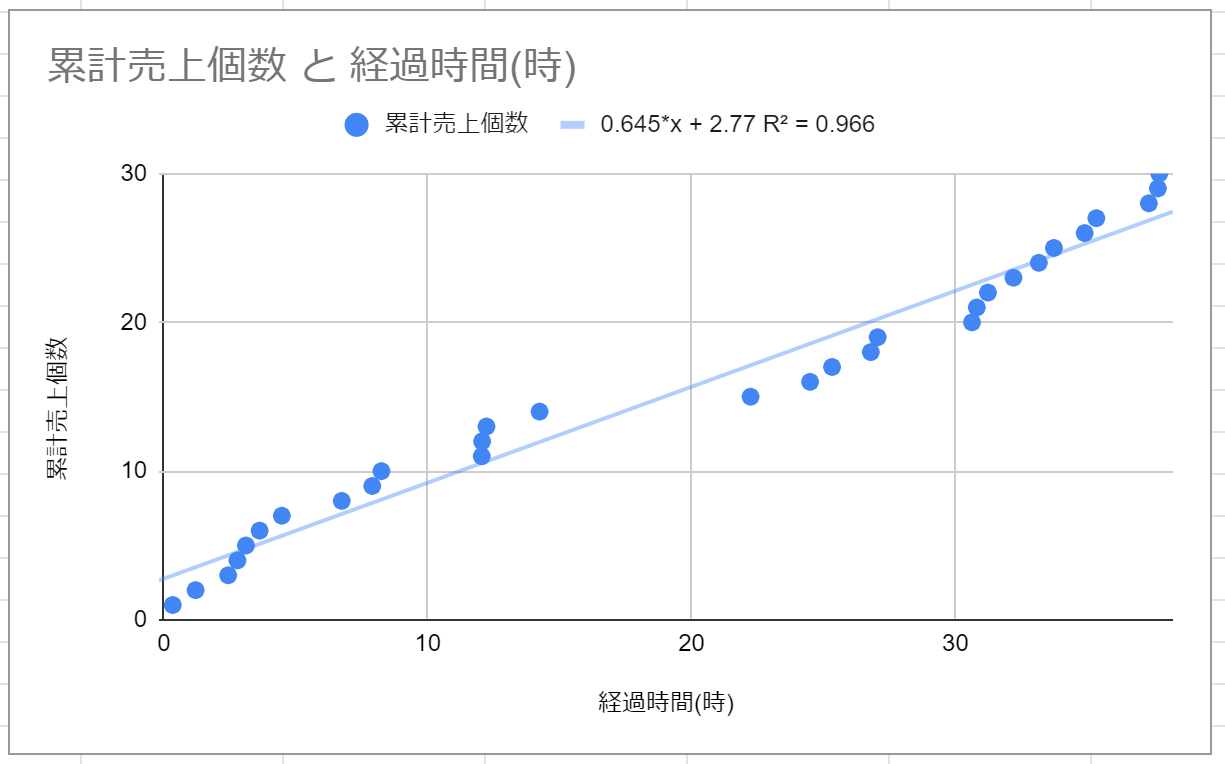
まず初めにGoogleSpreadSheetで売り上げの管理を始めました。そうすると、やはり「最終的に何冊売れるのか」ということが気になり始めました。そこで、横軸に経過時間、縦軸に累計売上個数のグラフを書いて、線形回帰させてみました。
すると、R^2=0.966という非常に決定係数の高いモデルが導かれました。しかし、これは正しいでしょうか?
今回は、数式で書くと
y = ax + b
というグラフです。今回、xには技術書典開会からの経過時間が入っています。ということは、10時間に6冊売れ、会期中(360時間)の間に216冊売れます。また、単価が1,000円です。そのため、この1冊だけで時給600円の不労所得を一生得られる計算になります。これは流石に現実味がないことが分かります。
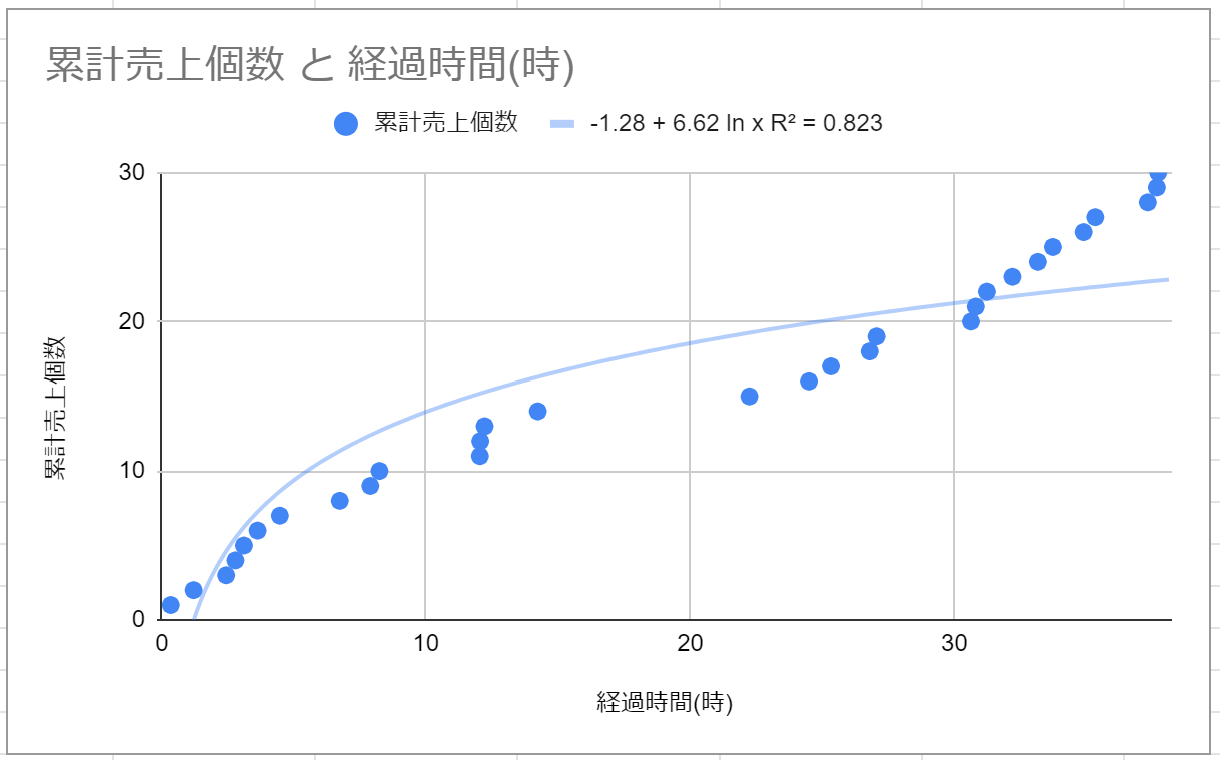
そこで、対数で近似してみました。
R^2=0.823なので、線形のグラフほどではありませんが、あてはまりは良いです。しかし、疑問な部分はあり、対数のグラフは0付近では負の値を取ります。これはどういう状況でしょうか?始まったとたん、私がどこかから自分で書いた本を仕入れているのでしょうか?また、線形ほどではありませんが、logの関数はx→∞のとき、値は∞になります。私の寿命が∞になることはないと思いますが、売り上げが∞になるのもおかしいと思いました。
このあたりで、じゃあ自分で数式モデル立てるかぁと思って作り始めたのが上記のnotebookになります。
指数分布っぽい関数による近似
天下り的に書きますが、今回は以下の関数で近似しています。
y = c(1-e^{-ax})
ここには2つの理由があります。1つめの理由は、
大抵、最初しか売れない。
これは自分の感覚値なのですが、最初の告知のタイミングが一番売れる。それ以降は、ぽつぽつとしか売れない。という印象があります。これをモデル化したい。というモチベーションがありました。
もう1つは、x→∞の時に収束する。という点です。これはある一定で売り上げが停滞することをモデル化したかった。という理由です。
自分がモデル化をするにあたり、頭に思いついたのは、
y = e^{-ax}
という関数です。
これは、告知の最初はよく売れ、時間が経つにつれて売れなくなってくる。という傾向を表現しようとしました。
しかし、これは"時間ごとの売り上げ"に過ぎません。したがって、開始1時間で10冊、開始2時間で8冊。開始3時間で5冊。という数字を与えるものです。しかし、今回、観測できる数字は、累計売上となります。開始1時間に10冊累計で売れている。開始2時間で18冊累計で売れている。開始3時間で23冊累計で売れている。というデータです。そのため、パラメーター推定する関数はこの関数を積分した形である必要があります。
そこで、思いついたのが指数分布です。
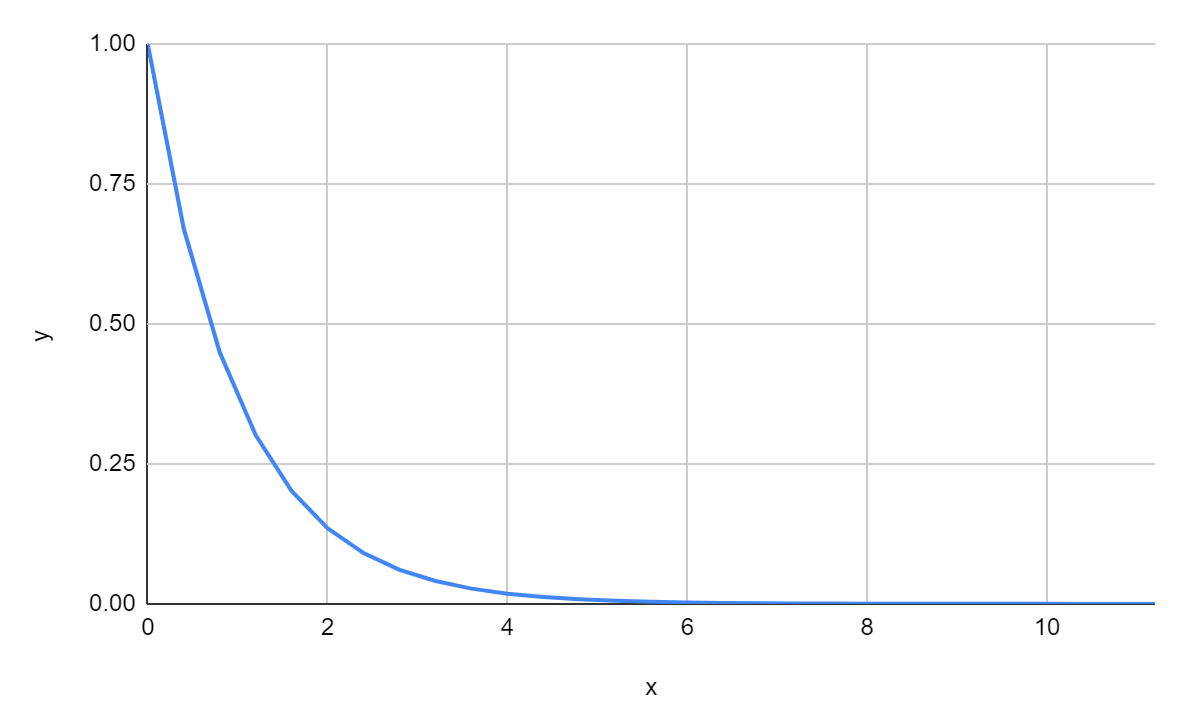
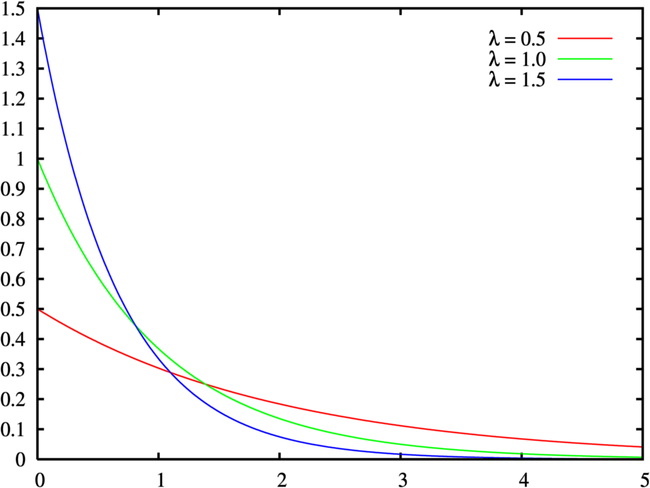
指数分布は確率密度関数が以下で計算されます。
f(x;\lambda) = \lambda e^{-\lambda x}
画像引用:指数分布
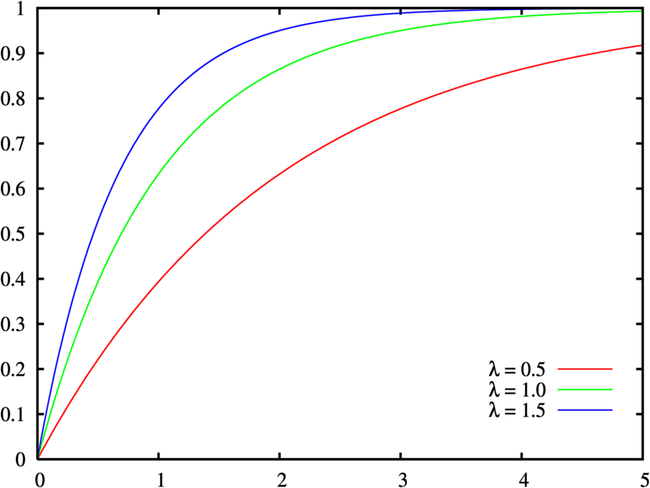
また、累積分布関数も数式で表されます。
f(x) = 1 - e^{-\lambda x}
画像引用:指数分布
ここで累積分布関数なのでx→∞のとき、f(x)=1となります。この性質は、この問題では売り上げが飽和するモデルと考えることができます。また、確率密度関数が、当初想定した減少する指数関数と一致するので、当初の目的とも合致しそうです。そのため、この式を少し変形し、
y = c(1-e^{-ax})
という数式を用いて、フィッティングを行いました。
予測精度を上げる工夫
notebookには以下のような関数が書かれています。
def add_latest_data(data):
now = datetime.now()
dt = (now + timedelta(hours=9) - start_time) #時差を合わせるため
last = dt.total_seconds()/(60.*60)
return data + [[last,data[-1][1]]]
これは、現在判明している売り上げのデータから、最新の売り上げ冊数を抽出します。
その売り上げ冊数と現在の時刻を、データの最後に追加する。ということをしています。
このようなチューニングをなぜ行っているかというと、ナイーブな数理モデルは予測値が上振れする。という問題がありました。
例えば、
- 月曜日に10冊売れて、火曜日に売り上げが10冊のままです。金曜日には何冊売れているでしょう?
- 月曜日に10冊売れて、木曜日に売り上げが10冊のままです。金曜日には何冊売れているでしょう?
1.の場合、火曜日に10冊と確認しているので、水、木と日付があるので、金曜日までに何冊か売れてる可能性はあるでしょう。しかし、2.の場合、もう金曜日まで日付が無いので、金曜日に11冊以上売れてる可能性は低いでしょう。
売り上げたタイミングでしかデータは追加しない方針の場合、「今、売れていない」ことがデータに入ってきません。そうすると予測値が上振れしてきます。
そこで、この現象を考慮し、"売れなかったというデータ"を追加するために、データの最後に最新の売り上げ冊数のデータを入れることで、上振れを防ぐというアーティファクトなチューニングをしています。
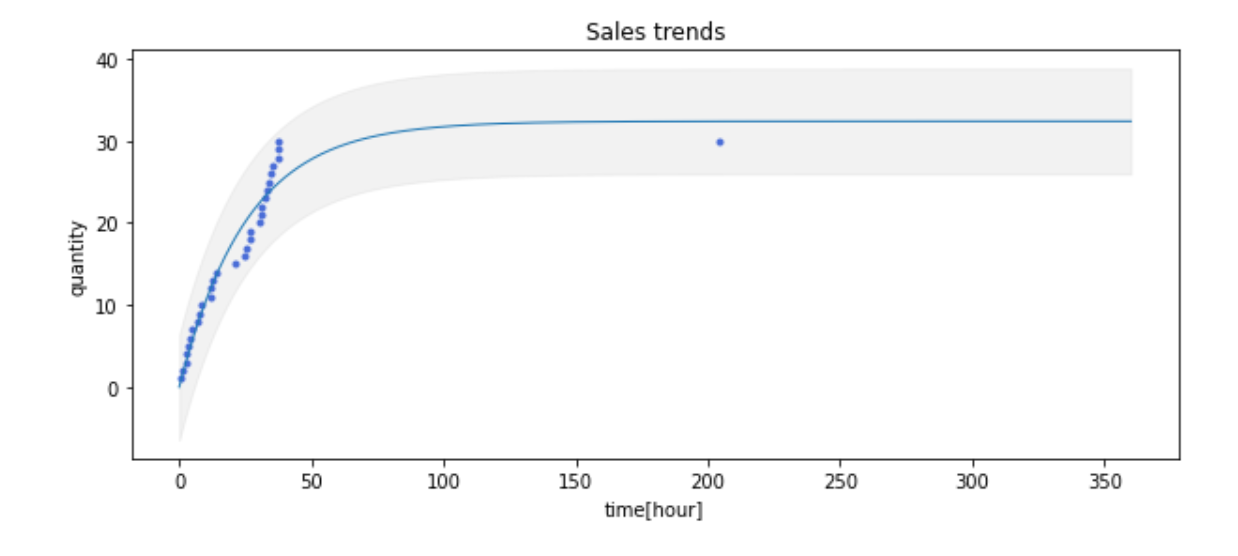
売り上げ冊数・最小値と最大値の予測
最終的な売れる冊数mについて計算しています。これは、推定した関数をfとしたとき、
m = f(15 \times 24)
と計算しています。受け取る次元が時間なので、会期の15日間の時間を渡しているだけです。
また、売れる最小値と最大値も推定しています。これも理屈としては簡単です。
予測した値と実際の値の差分から誤差を計算します。ここから標準偏差σを求めます。
そこから誤差を正規分布と仮定し、最小値はm-3σ,最大値はm+3σとして計算しています。
この値をグラフ上でもグレーの値として描画しています。
そして、誤差の情報から決定係数を計算しています。そして、現在の売り上げの冊数やモデルのパラメーターを出力して、予測結果と見比べられるようにしています。
感想
技術書典に初めて参加して、どれくらい売れるのか?というのは、非常に気になりました。
実際、会期が始まって、ぽつぽつ売れ始めると、ずっと気になり始め、何度も売り上げ履歴をリロードしたりするようになりました。
そこで、自分の気持ちを落ち着かせる意味もあって、数理モデルの作成をしました。結果、意外にいいモデルになったのかな。と思いました。
これは自分でモデリングしたという理由もあるかもしれませんが、割と納得感があります。
もう会期も半分ぐらいなので、だいぶ振れ幅が少なくなって、綺麗に収束が見えてきており、R^2も0.9以上あるので、着地の安心感も結構あります。
したがって、技術書典などで、売り上げがどれくらい出るかやきもきする方は、一度、データを入れて見て安心?してみてはいかがでしょうか。