zip圧縮で文章の著者推定ができるという都市伝説?を検証してみた。

#概要

ある小説家Aの文章を3編いれて、zip圧縮をする。
ある小説家Aの文章を2編、ある小説家Bの文章を1編入れて、zip圧縮をする。

このとき、前者の方が効率的に圧縮することができる。
この圧縮率の差からzip圧縮で著者推定ができる。

という話を聞いたことがあり、うすらぼんやりとした記憶があった。
久々にこの話を思い出したので、本当にできるのか？と思って、調査・検証を行ってみました。

#経緯

この話は、だいぶ昔でTwitter上で見た。
当時このツイートを見たとき、

「原理的には分かるが、若干ネタ臭がする嘘やろぉ」

と思っていた。

##「zip圧縮で文章の著者推定」の情報

自分の記憶だけでは怪しいので、元ネタについて調査した。
その結果、ネットで呆れるほど簡単に情報が見つかった

「同じ著者の小説をつなげてzip圧縮したら、複数の著者の小説をつなげて圧縮するよりも圧縮率がいいから著者推定に使える！」って論文が見つかった。キワモノかと思ったら精度いいし。論文探してるとしばしば「その発想はなかったわ」な物が見つかって面白いが俺は数日前にこれをやっとくべきだ。

引用：本の虫:まとめて圧縮すると著者推定できる話

引用したサイトによると普通に論文も出てきた

圧縮プログラムを応用した著者推定 ( pdf )

GoogleScholarで調べても情報がかなり少ない。引用論文は7つぐらいあった。

##論文を読む

論文を読んでいると、先行研究の記述があった

この手法に関する最も有名な研究として Dario Benedetto らの “Language Trees and Zipping”1) がある。これは米国物理学会の著名な 速報誌である Physical Review Letters 誌 2002 年 1 月 28 日号に掲載されたものである。
この文献中で 彼らは ZIP 系列の圧縮プログラムによる自動分類や類似データの同定手法を提案し、以下 ( Benedettoらの手法) DNA配列の類似度測定、言語不明データの言語識別 、著者不明データの著者推定に関する実験を行った結果を簡単に紹介している。著者推定に関しては 90 文献2) から構成されるコーパスに対して著者推定実験を行い、**93.3%**という高い精度を得ている。

この論文自体の被引用数は少なかったが、元論文の「Language Trees and Zipping」は200以上の引用数があった。ただ元々がPhysical Review Lettersなので、「zip圧縮による文章の著者推定ができる」という文脈で引用されているかは不明。

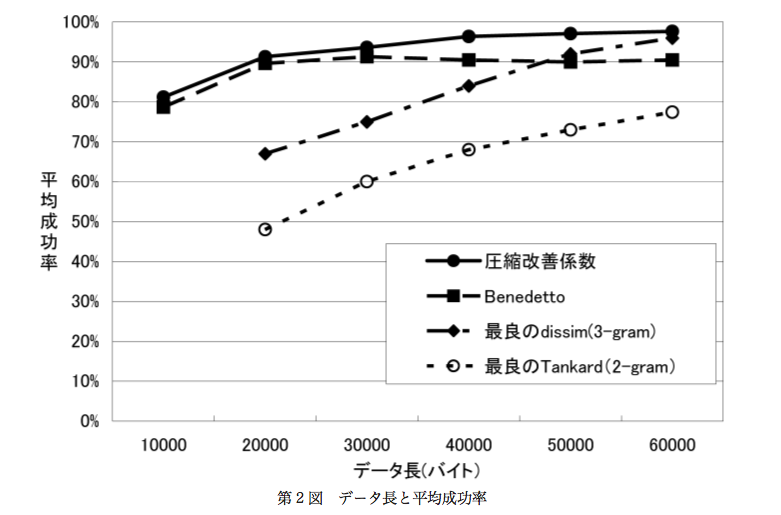
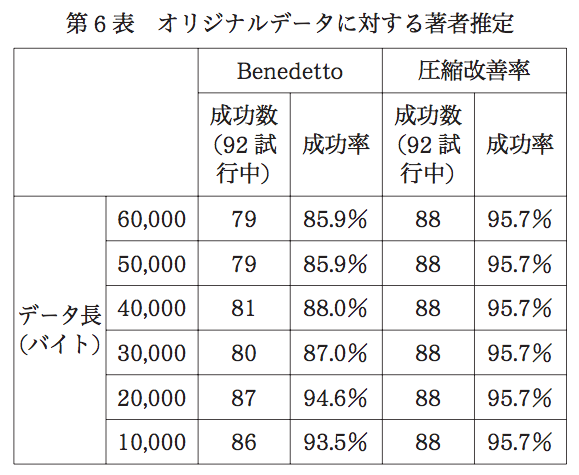
途中を省略し、結果のみを引用してくると

「Benedetto」が引用論文を元にした方法、「圧縮改善率」は、この論文で紹介されている方法。
ざっくりと書いてしまうと、

「zip圧縮により著者の推定に95.7%の精度で成功している」

やべぇ。。。

#自分で検証してみる
##モデル設計

それでも本当にできるとは信用していない。というわけで実際に自分でも検証して見た。

この記事では圧縮を以下のように考える。

LZ_{X} + LZ_{A} = LZ_{X \bigcup A} + \Delta_{X \bigcup A}

$LZ_{X}$は複数の文章の集合$X$の文章を圧縮した時のサイズ、$LZ_{A}$は文章の集合$A$の文章を圧縮した時のサイズ、$LZ_{X \bigcup A}$は文章群$X$と文章群$A$の和集合の文章を圧縮した時のサイズ。
$\Delta_{X \bigcup A}$は簡単に説明すると、文章群$X$と文章群$A$を合わせた文章を圧縮する時に、単体で圧縮するより、減少するサイズと定義できる。

この時、圧縮率$\rho$を定義する。

\rho = \frac{ LZ_{X \bigcup A} } { LZ_{X} + LZ_{A} }

文章を単体で圧縮するより、文章を合わせた方がどれくらい圧縮できるかを示す。

しかし、このままの圧縮率の定義では曖昧さがある。zip圧縮は文章の順番によって圧縮率が変わる。

pi@raspberrypi:/tmp/newtmp/test $ cat 芥川龍之介/羅生門.txt 芥川龍之介/鼻.txt > test2.txt
pi@raspberrypi:/tmp/newtmp/test $ cat 芥川龍之介/鼻.txt 芥川龍之介/羅生門.txt > test1.txt
pi@raspberrypi:/tmp/newtmp/test $ zip test1.zip test1.txt 
updating: test1.txt (deflated 54%)
pi@raspberrypi:/tmp/newtmp/test $ zip test2.zip test2.txt 
updating: test2.txt (deflated 54%)
pi@raspberrypi:/tmp/newtmp/test $ ls -la *.zip
-rw-r--r-- 1 pi pi   13127 Nov 11 12:10 test1.zip
-rw-r--r-- 1 pi pi   13110 Nov 11 12:10 test2.zip

そのため、今回の検証では少し条件を変更している。
今回は以下のようなアルゴリズムを用いている。

1. 著者Aの文章を99編ランダムに選択する
2. 著者Bの文章を1編ランダムに選択する
3. 著者Aの文書をランダムにシャッフルし、出力する。(textA)
4. 著者Bの文章をランダムにシャッフルし、出力する。(textB)
5. 著者A,著者Bの文書をランダムにシャッフルし、出力する(text)
6. textAを圧縮する(zipA)
7. textBを圧縮する(zipB)
8. textを圧縮する(zip)
9. zip,zipA,zipBから、圧縮率$\rho$を計算する。
10. 1-9を複数回計算し、平均の圧縮率$ \overline { \rho } $を計算する。

##検証

データを用意する。今回は、芥川龍之介と夏目漱石のデータを用いて行う。

青空文庫 作家別一括ダウンロード

以下のような実験を行う。

1. 芥川龍之介 99編, 芥川龍之介 1編
2. 芥川龍之介 99編, 夏目漱石 1編

という2つのパターンを実験する。もし著者推定ができるのであれば、1.の方が圧縮率が高いはずである。
今回は、10,000回実験を行う。

make_sample2() {
    l_filelistA=$1
    l_filelistB=$2

    work=`mktemp -d -p ./work`

    text=`mktemp -p $work "text.XXXXX"`
    textA=`mktemp -p $work "textA.XXXXX"`
    textB=`mktemp -p $work "textB.XXXXX"`

    cat $l_filelistA | sort -R | xargs cat > $textA
    cat $l_filelistB | sort -R | xargs cat > $textB
    cat $l_filelistA $l_filelistB | sort -R | xargs cat > $text

    zip=$work"/text.zip"
    zipA=$work"/textA.zip"
    zipB=$work"/textB.zip"
    
    zip $zipA -9 $textA > /dev/null
    zip $zipB -9 $textB > /dev/null
    zip $zip -9 $text > /dev/null
    
    text_size=`cat $text | wc -c`
    textA_size=`cat $textA | wc -c`
    textB_size=`cat $textB | wc -c`
    
    zip_size=`cat $zip | wc -c`
    zipA_size=`cat $zipA | wc -c`
    zipB_size=`cat $zipB | wc -c` 
    
    echo $authorA $authorB $text_size $textA_size $textB_size $zip_size $zipA_size $zipB_size

    rm -r $work
}

make_sample() {
    authorA=$1
    authorB=$2
    l_sample_num=$3
    l_source=$4
    l_target=$5

    root_work=`mktemp -d -p ./work`

    for i in `seq 1 $l_sample_num`
    do
        filelistA=`mktemp -p "$root_work" authorA_list.XXXXX`
        
        find $l_source -type f | sort -R | head -n $authorA > $filelistA
        
        filelistB=`mktemp -p "$root_work" authorB_list.XXXXX`

        find $l_target -type f | sort -R | head -n $authorB > $filelistB
    
        make_sample2 $filelistA $filelistB
    done

    rm -r $root_work
}



try_num=100
sample_num=100

source=$1
target=$2

mkdir work

a_num=99
b_num=1

for i in `seq 1 $try_num`
do
    make_sample $a_num $b_num $sample_num $source $target | while read line
    do
        echo `printf "sample-%03d-%03d-%03d" $a_num $b_num $i` $line
    done
done

これらを集計し、平均圧縮率を調べる。
また、もう１つ実験を行った。
それぞれのサンプルにおいて圧縮率を計算する。
実験ケースごとに圧縮率を組み合わせ比較し、それらの個数を計算した。

#結果

結果1.

実験対象	平均圧縮率$ \overline { \rho } $
芥川龍之介 99編, 芥川龍之介 1編	0.996695176
芥川龍之介 99編, 夏目漱石 1編	0.998729984

結果2.

実験対象	個数
芥川龍之介 99編, 芥川龍之介 1編の圧縮率 < 芥川龍之介 99編, 夏目漱石 1編の圧縮率	64,343,495
芥川龍之介 99編, 芥川龍之介 1編の圧縮率 >= 芥川龍之介 99編, 夏目漱石 1編の圧縮率	35,656,505

#考察

結果1.を見た時、平均圧縮率に関して芥川龍之介の方が圧縮率がわずかながら高かった。しかし、0.02%程度の差なので、実際のところ比較するのは難しい。
一方で結果2.の方を見ると大きな差が出た。それぞれのサンプルケースにおいて比較すると、芥川龍之介単著の方が圧縮率が高いケースが1.8倍程度観測できた。
そのため、**芥川龍之介と夏目漱石のケースにおいて、zip圧縮で著者推定を行うのは、できないわけではない。**という感触を得た。どうやら「zip圧縮で著者推定できる。」というのは嘘ではないらしい。

#感想

この話を聞いた時に、エラー検知に使えるのではないか？という発想になった。
新機能をリリースする前、した後のエラーログを溜め込んでおく。このリリース前後でzip圧縮率が変わるのであれば、理由はよくわからないが、バグが発生したことがわかり、新機能のリリースを止めてロールバックすることができるのではないかなぁ。と思っていました。
で、この話を知り合いに話したところ、いやいや、そんなこと無理だろ・・・という反応をもらって、まぁ私も「笑いのネタ」だと思って話していたので、大して気にもしていませんでした。
で、今週にこの話を、ふと思い出したので、ちょっとやってみました。多分簡単だし。と思って。でも、意外にかかりましたね。実験の機材がRasPiってのもあるのですが、zipするのにも結構コストがかかります。あと久々に論文を斜め読みする。ということをしました。そのせいで手順や実験がめちゃめちゃになったところもあって、辛かったです。。。論文はちゃんと読まなきゃ。。。