卒論でポアソン分布とガンマ分布を扱ったのでメモしておく。
ポアソン分布
ポアソン分布では単位時間あたり平均$λ$回発生するようなランダムな事象があるときに、時刻$t$までに$n$回起こる確率を表現することができる。
その確率を以下のように表せる。
P(n,t)=\frac{\mathrm{e}^{-{\lambda}t}({\lambda}t)^n}{n!}
実装は以下のようになる
python3を用いて実装を行なった。
import math
import matplotlib.pyplot as plt
# ポアソン分布を計算する
# 返り値は単位時間あたり平均λ回発生するようなランダムな事象があるときに、時刻tまでにn回起こる確率
def poisson_probability(n, t, lambda_poisson):
return math.e**(-lambda_poisson * t) * (lambda_poisson * t)**n / math.factorial(n)
# 累積ポアソン分布を計算する
# nは離散であるので積分は用いずΣを用いて計算する
# 返り値は単位時間あたり平均λ回発生するようなランダムな事象があるときに、時刻tまでに0,1,2,3,4...n回起こる確率
def cumulative_poisson_probability(n, t, lambda_poisson):
cumulative_probability = 0
for i in range(0, n + 1):
cumulative_probability += math.e**(-1 * lambda_poisson * t) * (lambda_poisson * t)**i / math.factorial(i)
return cumulative_probability
# ポアソン分布をプロットする
# x軸:n, y軸:確率
# 単位時間あたり平均λ回発生するようなランダムな事象があるときに、時刻tまでにn回起こる確率をnを変動させて出力する
def plot_poisson(time, lambda_poisson):
x_axis = np.linspace(0, 2 * time * lambda_poisson, 2 * time * lambda_poisson + 1)
y_axis = [poisson_probability(x, time, lambda_poisson) for x in x_axis]
plt.title('poisson time: {0} lambda: {1}'.format(time, lambda_poisson))
plt.xlabel('n')
plt.ylabel('probability')
plt.plot(x_axis, y_axis)
plt.savefig("poisson.png")
plt.show()
# 累積ポアソン分布をプロットする
# x軸:n, y軸:確率
# 単位時間あたり平均λ回発生するようなランダムな事象があるときに、時刻tまでに0,1,2,3...n回起こる確率をnを変動させて出力する
def plot_cumulative_poisson(time, lambda_poisson):
x_axis = np.linspace(0, 2 * time * lambda_poisson, 2 * time * lambda_poisson + 1)
y_axis = []
for x in x_axis:
y_axis.append(cumulative_poisson_probability(int(x), time, lambda_poisson))
plt.title('cumulative poisson time: {0} lambda: {1}'.format(time, lambda_poisson))
plt.xlabel('n')
plt.ylabel('probability')
plt.plot(x_axis, y_axis)
plt.show()
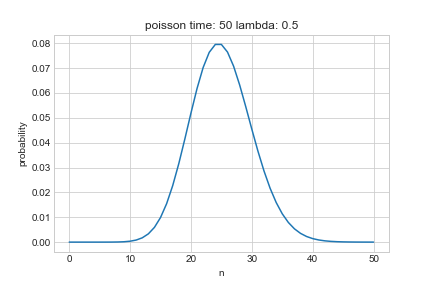
上図はポアソン分布である。単位時間あたり0.5回発生するランダムな事象は時刻50までに発生する回数の確率を表している。直感通り、$n=25$あたりでピークとなっている。
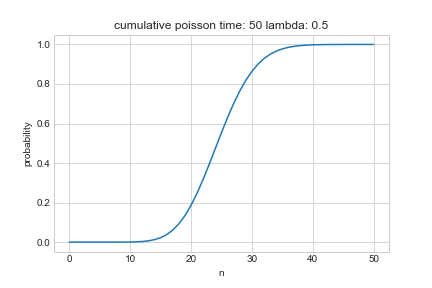
上図は累積ポアソン分布である。累積して確率の和は1に収束する。
ガンマ分布
ガンマ分布では単位時間あたり平均$λ$回発生するようなランダムな事象があるときに、時刻$tに$n$回目が起こる確率を表現することができる。
その確率は以下のように表せる。
f(n,t) = \frac{{\lambda}^n}{(n-1)!}t^{n-1}\mathrm{e}^{-{\lambda}t}
実装は以下のようになる
python3を用いて実装を行なった。
import math
import matplotlib.pyplot as plt
# ガンマ分布を計算する
# 返り値は単位時間あたり平均λ回発生するようなランダムな事象があるときに、時刻tにn回目が起こる確率
def gamma_probability(n, t, lambda_poisson):
return lambda_poisson**n * t**(n - 1) * math.e**(-lambda_poisson * t) / math.factorial(n - 1)
# 累積ガンマ分布を計算する
# 時間tは連続であるので積分を用いて計算する
# 返り値は単位時間あたり平均λ回発生するようなランダムな事象があるときに、時刻0~tにn回目が起こる確率
def cumulative_gamma_probability(n, T, lambda_poisson):
cumulative_probability, abserr = integrate.quad(lambda t: gamma_probability(n, t, lambda_poisson), 0, T)
return cumulative_probability!
# ガンマ分布をプロットする
# x軸:t, y軸:確率
# 単位時間あたり平均λ回発生するようなランダムな事象があるときに、時刻tにn回目が起こる確率をプロットする
def plot_gamma(n, lambda_poisson):
x_axis = np.linspace(0, 2 * n / lambda_poisson , 10 * n / lambda_poisson)
y_axis = [gamma_probability(n, x, lambda_poisson) for x in x_axis]
plt.title('gamma n: {0} lambda: {1}'.format(n, lambda_poisson))
plt.xlabel('time')
plt.ylabel('probability')
plt.plot(x_axis, y_axis)
plt.savefig("gamma.png")
plt.show()
# 累積ガンマ分布をプロットする
# x軸:t, y軸:確率
# 単位時間あたり平均λ回発生するようなランダムな事象があるときに、時刻0~tにn回目が起こる確率をプロットする
def plot_cumulative_gamma(n, lambda_poisson):
x_axis = np.linspace(0, 2 * n / lambda_poisson , 2 * n / lambda_poisson + 1)
y_axis = []
for x in x_axis:
y_axis.append(cumulative_gamma_probability(n, x, lambda_poisson))
plt.title('cumulative gamma n: {0} lambda: {1}'.format(n, lambda_poisson))
plt.xlabel('time')
plt.ylabel('probability')
plt.plot(x_axis, y_axis)
plt.show()
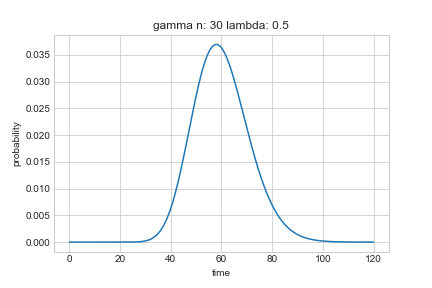
上図はガンマ分布である。単位時間あたり0.5回発生するランダムな事象が30回目に発生する時の確率を表している。直感通り、$t=60$あたりでピークとなっている。
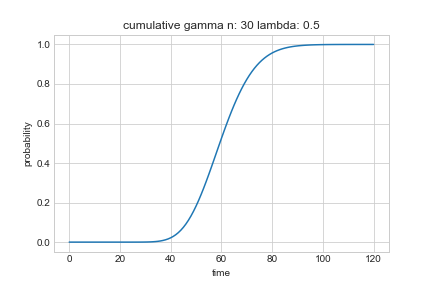
上図は累積ガンマ分布である。$t$は連続であるので積分を行うと確率の和は1に収束する。