この記事は、Ethereum Advent Calendar 2019の 18 日目です。
はじめに
昨日は Ethereum2.0 やコンセンサスアルゴリズムについて書きました。
Ethereum2.0 を例にしてコンセンサスアルゴリズムとは何か説明する
今回は、Ethereum2.0 のコンセンサスアルゴリズムについての研究を紹介する。
どのようにコンセンサスアルゴリズムが研究され改善する方向へ行くかが分かれば嬉しい。
Weighted Voting on the Blockchain: Improving Consensus in Proof of Stake Protocols
この論文は、2019 IEEE International Conference on Blockchain and Cryptocurrency (ICBC)で Best Paper になったものである。
この記事で使われている全ての図表はこの論文から引用している。
どんな研究
CasperFFG でのブロック検証やブロックファイナライズを対象にした研究である。
CasperFFG では、投票によってブロックファイナライズを行っている。
2/3以上が投票されたらファイナライズされる。
しかし、このプロトコルは誤ってまたは悪意を持って棄権した検証者に起因する障害に対して脆弱である。
そこで、この研究では重み付き投票とそれを実現するための仕組みを提案し、それが有効であることを数値シュミレーションで示されている。
どんな手法や技術
CasperFFGではブロックファイナライズにおいて66%以上の投票があればブロックが承認されるとされている。悪意ある検証者が40%いるとすると、66%以上の投票を得ることはできないのでシステムが期待通りの動作をしないことになる。そこで、重み付き投票を用いることで悪意ある検証者の重みを小さくし、善良な検証者の重みを大きくすることで悪意ある検証者に起因する障害に堅牢なシステムを作ると提案している。
ユーザのスコアを導入する。
あるユーザーのスコアは、初期値を0.5としmultiplicative weights updateという手法によって更新していく。正しい検証をすればスコアは上昇し、そうでなければ下がる。重みはスコアによって決定される。
どうやって評価した
モデリングを行い、数値シュミレーションにより評価する。

これは数値シュミレーションの結果であり、縦軸は重み付けされた有効な投票割合で横軸は時間である。
初期状態は悪意ある検証者が40%おり、有効な投票割合は60%である。
しかし、時間経過とともに検証者のスコアを更新していくと有効な投票割合は87%程度まで向上する。
青と赤の違いは、パラメータによる収束速度の違いである。
モデル詳細
時刻はタイムスロットtに分割できる。
t \in\{0,1,2, \ldots\}
時刻tに提案されたブロックを以下のように定義する。
1なら承認すべきブロック、0ならリジェクトすべきブロック
B_t \in \{0,1\}
検証者iは時刻tで投票するかどうかを選択できる。
投票するなら承認、しないならリジェクトという意思である。
X_{i, t}=\left\{\begin{array}{cl}{1,} & {\text { if validator } i \text { voted on the approval of the }} \\ {} & {\text { proposed block } B_{t} \text { in time slot } t} \\ {-1,} & {\text { otherwise }}\end{array}\right.
時刻tにおける検証者iのスコアを以下のよう定義する。
すなわち、正しく提案されたブロックを判断できる確率である。
p_{i, t}:=P\left(X_{i, t}=1 | B_{t}=1\right)=P\left(X_{i, t}=-1 | B_{t}=-1\right)
Committeeという投票を行う検証者の集合の効用は以下のように定義される。
Validなブロックを承認したら嬉しいし、Invalidなブロックをリジェクトしたら悲しいよねみたいな意味である。

multiplicative weights update (MWU) algorithmを使ったpの更新方法は以下で示される。
MWUという手法はこの論文で提案された方法ではなく以前からある手法である。
その手法をPoSのパラメータの更新に用いたという点は新しい。

arxivから引用したので本当にあってるか疑問に残る点がある。
\min \{1-\epsilon,(1+\delta)\}, \max \left\{0.5-\epsilon,(1-\delta)^{\ell_{r}}\right\}, \max \left\{0.5-\epsilon,(1-\delta)^{\ell_{a}}\right\}
ではなく
\min \{1-\epsilon,p(1+\delta)\}, \max \left\{0.5+\epsilon,p(1-\delta)^{\ell_{r}}\right\} ,\max \left\{0.5+\epsilon,p(1-\delta)^{\ell_{a}}\right\}
ではないか?多分
また、重みはスコアpを用いて以下のように定義する。
これもMWUと同様に既存研究からいい感じに引用している。
w_{i, t}:=\ln \left(\frac{p_{i, t}}{1-p_{i, t}}\right)
自分で実装してみた
Pythonで実装して数値シュミレーションを行ってみた。
import math
import random
class Validator():
def __init__(self, p, attacked):
# profile
self.p = p
# 攻撃されているかどうか
# 攻撃されているバリデータは投票できない
self.attacked = attacked
# MWU
def update_profile(self, x, b, delta, lr, la):
if x == b:
self.p = min(self.p * (1+delta), 0.99999)
elif b == 1:
self.p = max(self.p * ((1-delta)**lr), 0.50001)
else:
self.p = max(self.p * ((1-delta)**la), 0.50001)
# 重み
def weight(self):
return math.log(self.p) - math.log(1.0-self.p)
# pから投票を推定する
def p_to_decision(self, proposed_block):
if self.attacked: return -1
return proposed_block if self.p > random.random() else -1 * proposed_block
# バリデータ
# 正答率が正規乱数に従うn人のバリデータを生成
def create_validators(mean, var, n, attacked_rate):
attacked_validator_count = int(n * attacked_rate)
aps = np.random.normal(mean, var, attacked_validator_count).tolist()
attacked_validators = list(map(lambda p: Validator(max(min(0.99999, p), 0.50001), True), aps))
non_attacked_validator_count = n - attacked_validator_count
nps = np.random.normal(mean, var, non_attacked_validator_count).tolist()
non_attacked_validators = list(map(lambda p: Validator(max(min(0.99999, p), 0.50001), False), nps))
validators = attacked_validators + non_attacked_validators
random.shuffle(validators)
return validators
# 重み付き投票のシュミレーション
import random
%matplotlib inline
import matplotlib.pyplot as plt
# パラメータ
alpha = 0.5
delta = 0.001
la = 12
lr = 0.01
# return: 攻撃されていないvalidatorの重み / 全てのvalidatorの重み
def weighted_approval_votes(validators):
non_attacked_validator_weight = 0
all_validator_weight = 0
for validator in validators:
w = validator.weight()
all_validator_weight += w
if not validator.attacked:
non_attacked_validator_weight += w
return non_attacked_validator_weight / all_validator_weight
def weighted_approval_votes_changes(times, validators):
result = []
for t in range(times):
result.append(weighted_approval_votes(validators))
# 提案されたブロックを定義
proposed_block = 0 if alpha > random.random() else 1
# 実際に投票を行いprofileを更新する
for validator in validators:
# 攻撃されている場合、投票することができない
if validator.attacked: continue
if validator.p > random.random():
# 正しく投票のとき
validator.update_profile(proposed_block, proposed_block, delta, lr, la)
else:
# 間違った投票のとき
validator.update_profile(-proposed_block, proposed_block, delta, lr, la)
return result
def plot_weighted_approval_votes(times, validators):
x_axis = list(range(times))
y_axis = weighted_approval_votes_changes(times, validators)
plt.title('weighted approval votes')
plt.xlabel('times')
plt.ylabel('weighted approval votes')
plt.plot(x_axis, y_axis)
plt.savefig("plot_weighted_approval_votes.png")
plt.show()
# 実行
vs = create_validators(0.9, 0, 100, 0.4)
plot_weighted_approval_votes(500, vs)
正しいブロックが提案される確率50%(コード中のalpha)、正しいブロックを承認する嬉しさを1,正しいブロックをリジェクトする嬉しさ-0.01(コード中のl_r),不正なブロックを承認する嬉しさ12(コード中のl_a)、不正なブロックをリジェクトする嬉しさ1とすると以下のようになる。
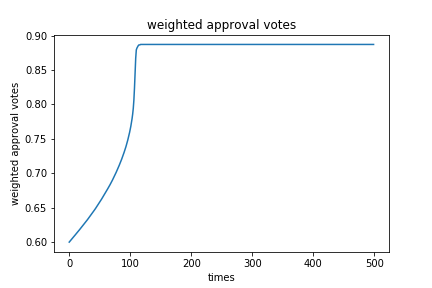
それっぽい図ができた。
さいごに
長くなってしまったので説明を省いたのだが、有効な投票割合が上がるので当たり前といえば当たり前であるが重み付き投票によって全体の効用も向上する。
それに関するモデリングもあったが省略した。
このように既存手法の組み合わせでコンセンサスアルゴリズムの改善が提案がされており面白い。
説明が雑になっていって訳がわからないかもしれないけれど、気楽にコメント等いただけたら嬉しい。
おすすめ論文
Eyal, Ittay, and Emin Gün Sirer. "Majority is not enough: Bitcoin mining is vulnerable." Communications of the ACM 61.7 (2018): 95-102.
Bitcoin において 51%ではなく 33%で攻撃できるSelfish miningという攻撃についての論文で読みやすくて結構面白い。