「精度」と「モデルの複雑さ」に注力しながら、線形回帰をpythonで実装。
目次
- 線形モデル
- 線形モデルによる回帰
- 線形回帰(通常最小二乗法)
- 一次元データに対しての線形回帰
- 高次元データに対しての線形回帰
参考文献
線形モデル
線形モデルは、入力特徴量の線形関数(Linear function)を用いて予測を行う。
線形モデルによる回帰
回帰問題で使われる線形モデルの予測式は、以下のようになる。
$$y = w(0) \times x(0) + w(1) \times x(1) + w(2) \times x(2) + ・・・ + w(p) \times x(p)$$
ここでの$x(0)~x(p)$は、ある1サンプルの特徴量を示す。また、$w$と$b$は、学習されたモデルのパラメータであり、$y$はモデルからの予測である。
特徴量が1つの場合、傾き$w(0)$、切片が$b$の直線になる。
回帰における線形モデルにおいての予測は、特徴量が1つの場合は直線に、特徴量が2つの場合は平面に、高次元の場合は超平面になる。
回帰モデルを用いた回帰には、様々なアルゴリズムが存在する。
それらの異なる点は2つ。
- パラメータwとbを訓練データから学習する方法
- モデルの複雑さを制御する方法
線形回帰(通常最小二乗法)
線形回帰(または、通常最小二乗法 ordinary least squares: OLS)は、最も単純な線形回帰手法である。
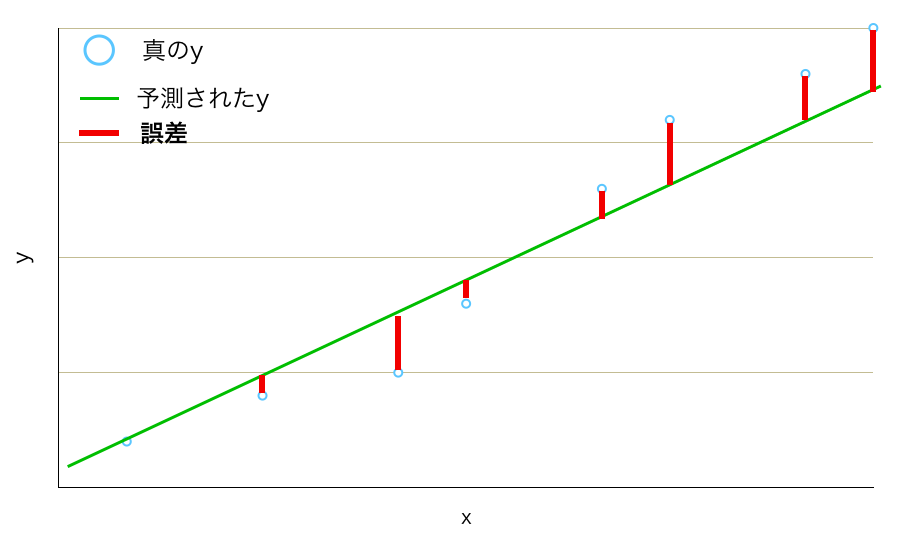
線形回帰は、訓練データにおいて、予測と真の回帰ターゲットyとの平均二乗誤差(mean squared error: MSE)が最小になるような$w$と$b$を求める。
平均二乗誤差は、
$$MSE = \frac{1}{n} \sum_{n=0}^{p} (y − \hat{y})^2$$
誤差をイメージできない人もいると思います(僕は頭に描けなかった)。なので、誤差を図示してみました。
線形回帰は、ハイパーパラメータがない。よって、モデルの複雑さを制御できない。
下準備
$ pip install scikit-learn
$ pip install mglearn
一次元データに対しての線形回帰
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import mglearn
X, y = mglearn.datasets.make_wave(n_samples=60)
print("(サンプル数, 特徴量数): ", X.shape)
# => (サンプル数, 特徴量数): (60, 1)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
lr = LinearRegression().fit(X_train, y_train)
print(f"training dataに対しての精度: {lr.score(X_train, y_train):.2}")
print(f"test dataに対しての精度: {lr.score(X_test, y_test):.2}")
# => training dataに対しての精度: 0.67
# => test dataに対しての精度: 0.66
考察:
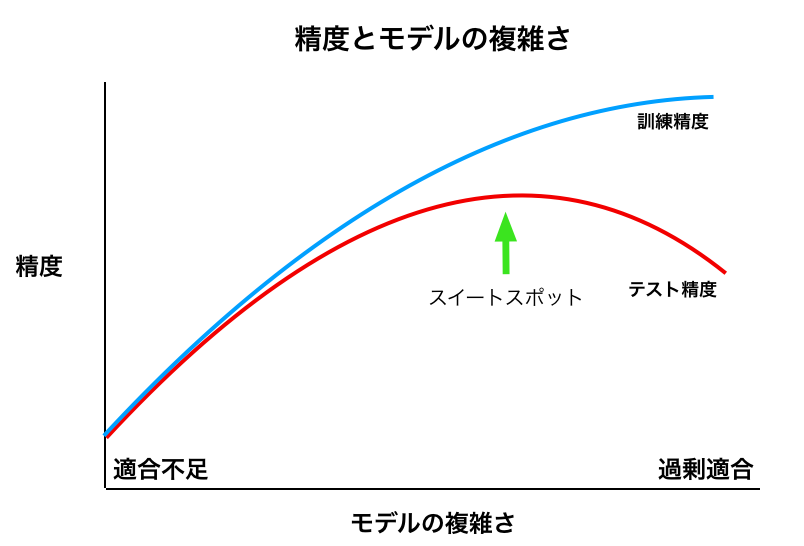
training dataに対しても、test dataに対しても、精度は低い。よって、過剰適合はなく、適合不足である可能性が高い。
下の「精度とモデルの複雑さ」の図でいうと、スイートスポット左側に位置しているのだろう。
線形回帰は、一次元データに対しては、モデルの複雑さが低く、適合不足に陥りやすい。
高次元データに対しての線形回帰
X, y = mglearn.datasets.load_extended_boston()
print("(サンプル数, 特徴量数): ", X.shape)
# => (サンプル数, 特徴量数): (506, 104)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
lr = LinearRegression().fit(X_train, y_train)
print(f"training dataに対しての精度: {lr.score(X_train, y_train):.2}")
print(f"test dataに対しての精度: {lr.score(X_test, y_test):.2}")
# => training dataに対しての精度: 0.95
# => test dataに対しての精度: 0.61
考察:
training dataに対しての精度は非常に良いが、test dataに対しての精度は良くない。これは、過剰適合の可能性が高い。
上記の「精度とモデルの複雑さ」の図でいうと、スイートスポットの右側に来ているのだろう。
よって、汎化性能(test dataに対しての精度)を上げるためには、モデルの複雑度を制御する必要がある。
その手法に、リッジ回帰とLassoがある。
おまけ
次の記事で、モデルの複雑さを制御する手法であるリッジ回帰とLassoについての記事を書く予定です。