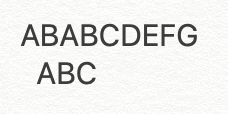文字列探索とは
ここまでは数列からの探索や、数列を期待通りにソートするなど、
数字を中心に扱ってきましたが、次に文字列を扱う探索を学んでいきたいと思います!
文字列探索というのがどういうことかという話なんですが、
ある文字列中とは別の文字列が含まれているかどうかを調べ、含まれていれば、その位置も調べるということです。
例えば、STRINGという文字列からINGを探索すれば、それは含まれていることになり、
文字列中の4番目に位置しているということになります。
探索される側の文字列はテキスト、探索する文字列をパターンと呼ばれることが多いようです。
今回はその文字列探索の中でも基礎的な力まかせ法について見ていきましょう。
力まかせ法とは
力まかせ法とは、その名の通り、
パターンが現れるまで、テキストを頭からひたすら走査していくという、
効率もへったくれもない筋肉質なアルゴリズムのようです。。笑
テキストが ABABCDEFG で、パターンが ABCとしたら、
最初の ABAと比較し、合ってなかったら1文字ずつずらして照合していくというのを繰り返していきます。
数列であれば前から一つずつ値を比較して確認する線形探索にも似ているため、
単純法や素朴法とも呼ばれるそうです。
ABABCDEFGで実際に流れを見てみると、まずは頭からパターンと照合してみます。
パターンの2文字目までは合致しましたが、3文字目が異なったので、
次にテキストの2文字目から照合します。
パターンの1文字目から一致しなかったので、テキストの3文字目から照合します。

3文字目から照合したところ、パターンの全てと一致したので、ここで初めて探索成功となります。
しかし、見て分かる通り、パターンと照らし合わせる際に合わなければ
テキストとの比較はリセットされて、1文字ずつしか前進することができないので、その点は非効率かもしれませんね。。
流れは掴めたので、実際にコードに落とし込んでみましょう!
コードに落とし込んでみる
static int bfMatch(String target, String pat) {
int pt = 0; // targetをなぞるカーソル
int pp = 0; // patをなぞるカーソル
while (pt != target.length() && pp != pat.length()) {
if (target.charAt(pt) == pat.charAt(pp)) {
pt++;
pp++;
} else {
pt = pt - pp + 1;
pp = 0;
}
}
if (pp == pat.length()) { // 探索成功
return pt - pp;
}
return -1; // 探索失敗
}
文字列targetから文字列patを探索し、成功した場合は、patと一致するtargetのインデックスを返します。
文字列target中に文字列patが複数含まれる場合は、一番最初にくる位置のインデックスを返すようにしています。
targetを走査するカーソルをpt、patを走査するカーソルをpp として、最初のインデックスである0で初期化しています 。
その後、 pt がtargetの文字列の長さと同じ かつ ppがpatの文字列の長さと同じ
になるまでwhile文を繰り返します
patが見つかるまで走査するか、そのままtarget全ての走査が終われば探索は終了なので
どちらかがtrueとなれば、探索のwhile文を抜けます。
一番最初の流れは、if文内で
target.chartAt(0) == pat.charAt(0)として1文字目が一致していれば
targetとpatのカーソルを1個ずつ増やしていき、走査対象を前へと進めます。
もし一致していなければ、targetのカーソルを patと合わせて進んだ分の次の要素に合わせたいので、
pt - pp + 1としています。
そして、patのppは最初へと戻していく という繰り返しです。
while文を抜けた後、ppが patの文字列の長さと一致していれば
ppが全て一致する文字列がtargetの中にあったということになるので、
ptが進んだカーソルから、パターン分の文字数を引いて、
パターンと一致した箇所の最初のインデックスを返すようにしています。
もしそうでなければ探索失敗として -1を返しています。
例えば、ABAABCというテキストから、ABCというパターンを探索するとなると、
target に ABAABCを pat にABCが渡されたあと、pt も pp も0から始まります。
target.chartAt(0) == pat.charAt(0) として A同士で一致します
そのままpt と ppをインクリメントして
target.chartAt(1) == pat.charAt(1) としてB同士で一致します
そのままpt と ppをインクリメントして
target.chartAt(2) == pat.charAt(2) としてAとCなのでここで
ptのカーソルは2-2+1で1に戻り、ppは0からとなります
target.chartAt(1) == pat.charAt(0) としてBとAなのでここで
ptのカーソルは1-0+12に戻り、ppは0からとなります
target.chartAt(2) == pat.charAt(0) ` としてAとAなのでここで
そのままpt と ppをインクリメントして
target.chartAt(3) == pat.charAt(1) としてAとBなのでここで
ptのカーソルは3-1+1で3に戻り、ppは0からとなります
target.chartAt(3) == pat.charAt(0) としてAとAなのでここで
そのままpt と ppをインクリメントして
target.chartAt(4) == pat.charAt(1) としてBとBなのでここで
そのままpt と ppをインクリメントして
target.chartAt(5) == pat.charAt(2) としてCとCなのでここで
そのままpt と ppをインクリメントすると
ptは6となり、targetの文字列長と一致し
ppも3となり、patの文字列長さと一致するので、ここでwhile文を抜けます。
その後、ppとpatの文字列長さが一致するので、そのまま
ptからppを引いて、一致する文字の最初のインデックスである3を返す という流れになりますね!
テキストの文字列がnとして、パターンの文字数がmであるとして、
力まかせ法の計算量はO(mn)で、実質的にはO(n)なので、力まかせというものの、そこまで遅いというわけではなさそうです。。
学んだこと
- 文字列探索の基礎に力まかせ法というのが存在し、その名の通り頭かひたすら照合を繰り返す。
- 照合するパターン側は一致しなければリセットされるので、その分は非効率になりやすい。
これまでの探索はkeyとなる数字を見つけてきたり、昇順に数列をソートしたりというのが多かったので
セットとなる文字列を探索するというのはなかなか新鮮でした。。!
力まかせな部分をより効率化したKMP法というのがあるらしいので、引き続き頑張っていきます!