マージソートとは
等間隔で単純挿入ソートを繰り返すシェルと、枢軸よりも大きいか少ないかで交換を行うクイックソートは
共に隣り合う値以外の交換も発生するので、不安定なアルゴリズムでしたが、
今回は隣り合う値同士の交換のみのマージソートについて学んでいきたいと思います。
マージなので色々と合わせるのかなと思いましたが、実際は
配列を前半部と後半部の2つに分け、
それぞれをソートしたものをマージする作業を繰り返すことによってソートを行うアルゴリズム
というものらしいです。。
全体を2つに分けてそれぞれをソートして、最終的に合成することを繰り返せば良いっぽいですね。
実際にイメージで理解していきましょう。
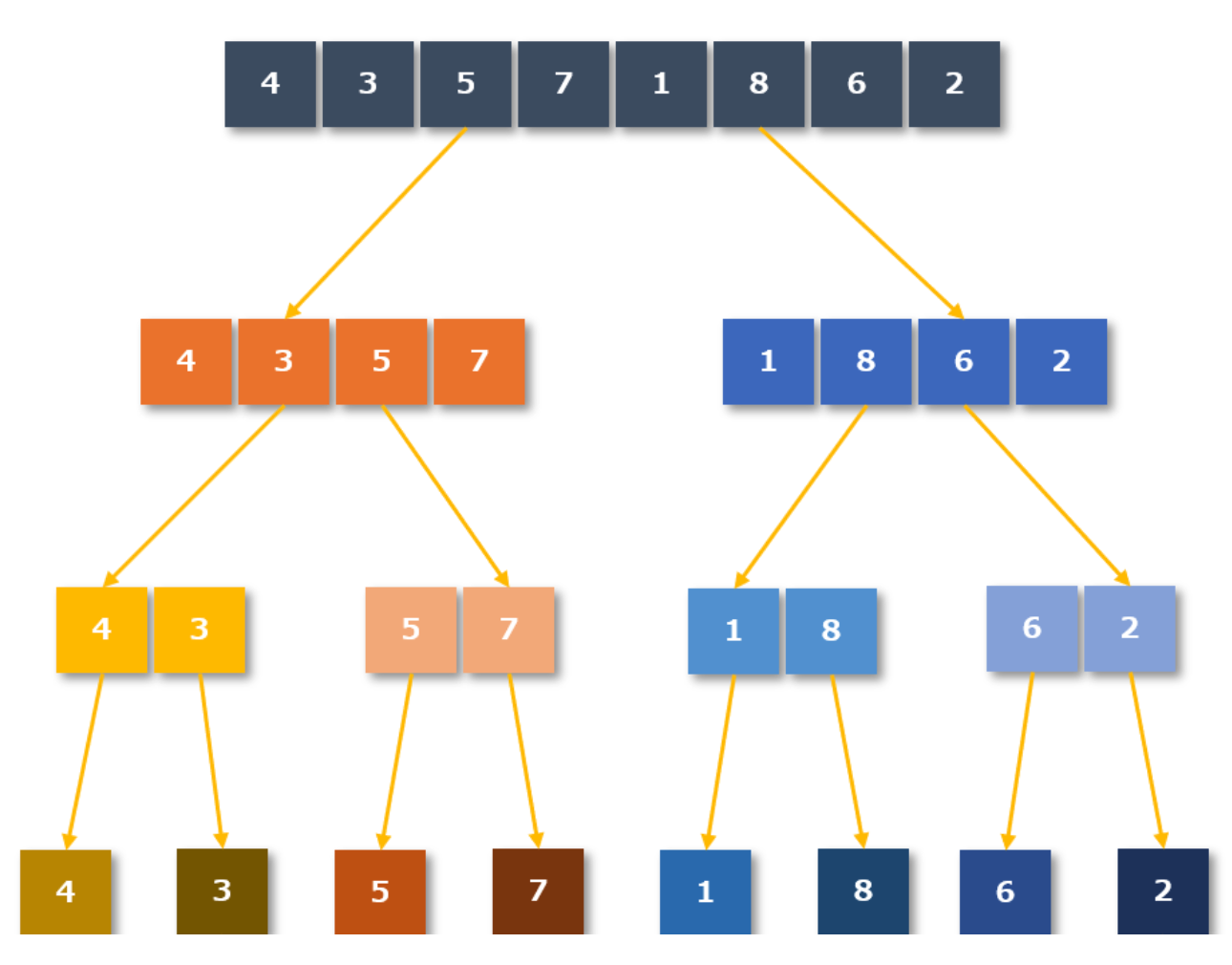
{4,3,6,7,1,8,6,2}という数列をマージソートしてみます。
分割自体は要素数が1になるまで繰り返すので、それぞれが1桁になるまで分割します。
次に分割した要素を戻していきますが、
ただ戻すだけでは、元の数列に戻すだけなので、ここで並び替えをしながら戻してみましょう。
① 1要素に分割された値:「4」「3」「5」「7」「1」「8」「6」「2」
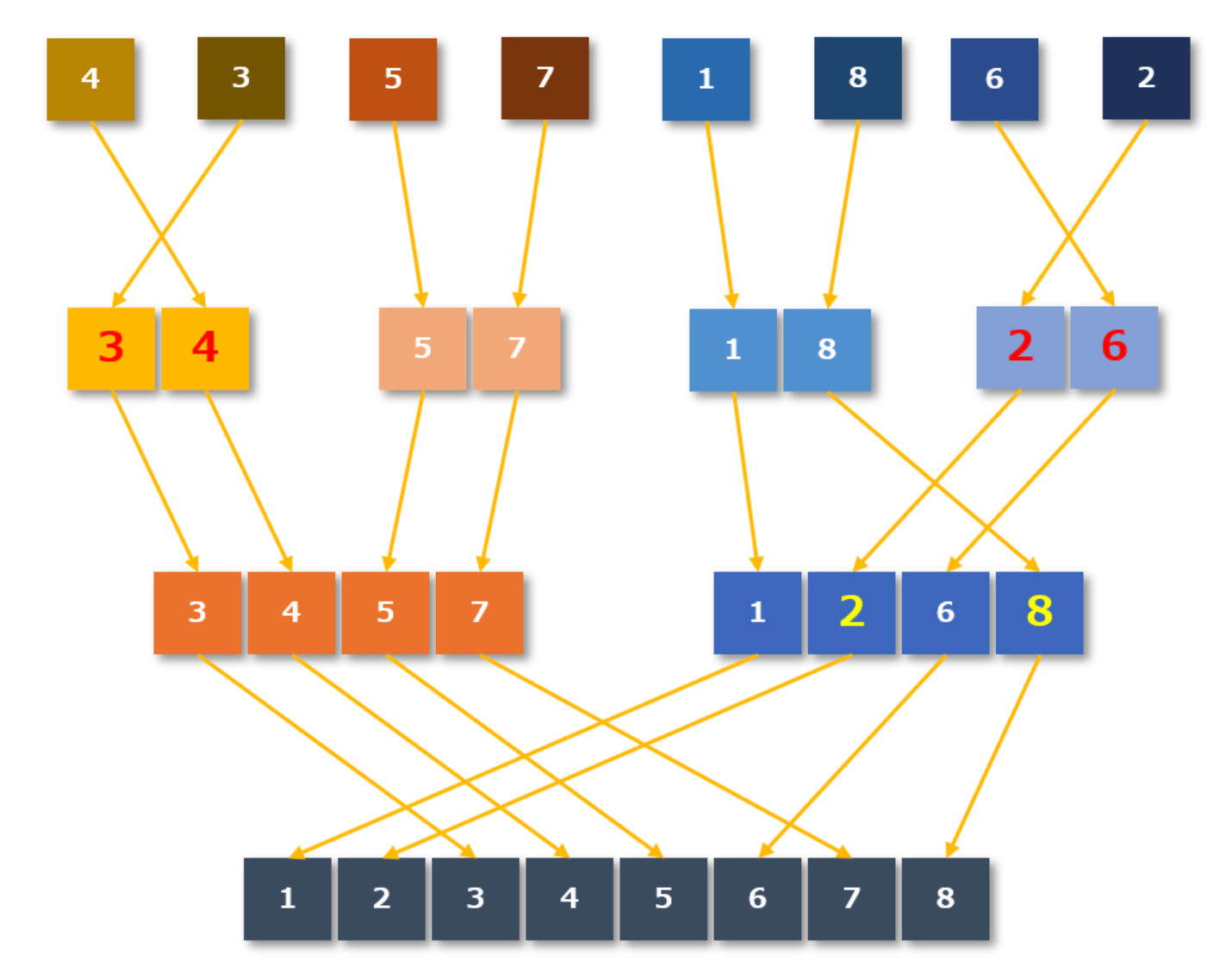
② 並び替えながら戻す:「3,4」「5,7」「1,8」「2,6」
③ 並び替えながら戻す:「3,4,5,7」「1,2,6,8」
④ 並び変えながら戻す:「1,2,3,4,5,6,7,8」
こうすることで、最終的に昇順にソートすることができました。
とはいえ、ソートしながら並びを戻すというのをどうコードで表現していくのか
という話なので、まずは分割した要素をマージするという部分から考えてみましょう。
マージとは
先ほどのイメージでも、マージ済みの配列を合成する際にも、小さいの方の値を
前方に持ってくるソート作業を同時に行い、合成していたので、
2つのソート済みの配列のマージというのは、
各配列の着目要素の値を比較し、小さい方の値を持つ要素を取り出して、第3の配列に格納する作業
であるということが言えそうです。
ここでいう第3の配列がマージ後のソート済みの配列ということになります。
2つのソート済みの数列があったとして、それぞれの配列を先頭から走査し
小さい方の値の要素を第3の配列に追加していくという流れを実際にコードで再現してみましょう。
static void merge(int[] a, int na, int[] b, int nb, int[] c) {
int pa = 0;
int pb = 0;
int pc = 0;
while (pa < na && pb < nb) // 2つの配列のうち、小さい方の値を配列cに格納
c[pc++] = (a[pa] <= b[pb]) ? a[pa++] : b[pb++];
while (pa < na) {
c[pc++] = a[pa++]; // aに残った要素をコピー
}
while (pb < nb) {
c[pc++] = b[pb++];// / bに残った要素をコピー
}
}
aがソート済み配列の1つ目、その要素数がna
bがソート済み配列の1つ目、その要素数がnb
cがマージ後の配列としたときに
aの配列を{2,4,6,8,11,13}
bの配列を{1,2,3,4,9,16,21} として、
2つの数列をマージしてみましょう。
まずは a[0]の2 と b[0]の1 で比較して、
もし、a[0]の方が小さければa[0]の値を、bの方が小さければb[0]の1を配列cに追加します
ここでは、 b[0]の方が小さいので、1を配列cに追加し、
小さかった方の要素を持つ配列、ここでは配列[b]のカーソルのみ次の要素に移行するという流れになります。
互いの配列のカーソルを移動して、どちらかのカーソルが末尾を超えた場合は
while(pa < na && pb < nb)(インデックスが要素数になった場合)は
比較する値がなくなるので、そのまま次のwhile文へ移行します。
cには[1]のみが追加されていて、そのまま続きを見ていくと、
a[0]の2と b[1]の2は同じ値なので、a[0]の2をcに追加します
a[1]の4とb[1]の2はb[1]の方が小さいので、b[1]の2をcに追加します
a[1]の4とb[2]の3はb[2]の方が小さいので、b[2]の3をcに追加します
a[1]の4とb[3]の4は同じ値なので、a[1]の4をcに追加します
a[2]の6とb[3]の4はb[3]の方が小さいので、b[3]の4をcに追加します
a[2]の6とb[4]の9はa[2]の方が小さいので、a[2]の6をcに追加します
a[3]の8とb[4]の9はa[3]の方が小さいので、a[3]の8をcに追加します
a[4]の11とb[4]の9はb[4]の方が小さいので、b[4]の9をcに追加します
a[4]の11とb[5]の16はa[4]の方が小さいので、a[4]の11をcに追加します
a[5]の13とb[5]の16はa[5]の方が小さいので、a[5]の13をcに追加します
この時点で、(pa(6) < na (6))ではなくなり、aには要素が残っていないことを表すので、
次のwhile文に移行します。 あとは、残った方の要素をインデックスを進めながら格納していくだけです。
while (pa < na)はfalse、(配列aには値が残っていない)while(pb(5) < nb(7))はtrueとなり、
b[5]の16、b[7]の21がcに追加され、{1,2,2,3,4,4,6,8,9,11,13,16,21}となり、マージが完了します。
3つの繰り返し文が並べられただけの単純なアルゴリズムで実現されるため
、
マージに要する時間計算量はO(n)らしいです。
このソート済配列をマージする方法を応用したのがマージソートということなので、
実際にマージソートをコードに落とし込んでいきます。
コードに落とし込む
例えば、まだマージされていない{5,6,4,8,3,7,9,0,1,5,2,3}という数列で考えてみましょう。
まず、配列を前半部と後半部の2つに分割します。
ここでは要素数は12なので、6個ずつの配列に分割します。
前半部と後半部のそれぞれをソートし、それらを先ほどの方法でマージすれば配列全体がソートできそうです。
{5,6,4,8,3,7}→ ソート後{3,4,5,6,7,8}
{9,0,1,5,2,3}→ ソート後{0,1,2,3,5,9}
ソート後の配列をマージすると、{0,1,2,3,3,4,5,6,7,8,9}
ということになります。
前半部と後半部に分けた配列のソートも全く同じ手続きで行い、
{9,0,1,5,2,3}→{9,0,1}と{5,2,3}としてソートすると
{0,1,9}と{2,3,5}となるので、マージすると{0,1,2,3,5,9}となります。
分割後のソートも同じ手続きになるので、整理すると次のようになります。
配列の要素数が2以上であれば、以下の手続きを適用する。
- 配列の前半部をマージソートによってソート
- 配列の後半部をマージソートによってソート
- 配列の前半部と後半部をマージ
これを繰り返せばいいので、実際にコードに落としてみましょう。
//--- マージソート ---//
static void mergeSort(int[] a, int n) {
buff = new int[n]; // 作業用配列を生成
__mergeSort(a, 0, n - 1); // 配列全体をマージソート
buff = null; // 作業用配列を解放
}
//--- a[left]~a[right]を再帰的にマージソート ---//
static void __mergeSort(int[] a, int left, int right) {
if (left < right) {
int i;
int center = (left + right) / 2;
int p = 0;
int j = 0;
int k = left;
__mergeSort(a, left, center); // 前半部をマージソート
__mergeSort(a, center + 1, right); // 後半部をマージソート
for (i = left; i <= center; i++) { //前半部分をbuffにコピー ①
buff[p++] = a[i];
}
while (i <= right && j < p) { //後半部分とbuffをマージ ②
a[k++] = (buff[j] <= a[i]) ? buff[j++] : a[i++];
}
while (j < p) { //buffに残った要素をaにコピー ③
a[k++] = buff[j++];
}
}
}
実際にマージソートの処理を行っているのは __mergeSortメソッドですが
メソッド内では以下のようなことを行っています。
- マージ結果を一時的に格納するための作業用配列buffを生成
- ソート作業を行うメソッド__mergeSortの呼び出し
- 作業用配列を解放・破棄
__mergeSortメソッドの引数には、ソート対象の配列aと、
その配列の先頭、末尾インデックスをleftとrightで渡しています。
メソッド全体は if(left < right)で囲っているので、
先頭インデックスよりも、末尾インデックスの方が大きい場合(要素が2以上)の場合のみ処理を行うようにしています。
一番最初に行う処理は、前半部a[left]~a[center]と後半部a[center+1]~a[right]の
それぞれに対して、再帰的に __mergeSortを適用することです。
ソート済みになった前半部と後半部のマージは、作業用配列のbuffを使って行います。
for (i = left; i <= center; i++) にて
配列の前半部a[left]~a[center]をbuff[0]~buff[center - left]にコピーします。
for文終了時のpの値は、コピーした要素の個数となり、center - left + 1となります。
while (i <= right && j < p)では、
配列の後半部a[center + 1] ~ a[right]と、
buffにコピーした配列の前半部のp個をマージして、そのマージ後の配列をaに格納しています。
while (j < p)にて、
配列buffに残った未格納部分の要素を配列aにコピーしています。
実際に{6,5,4,3,2,1}という数列で流れを追ってみましょう。
最初に__mergeSort(a,0,6-1)として呼ばれ、
__mergeSort内はif (left < right)で囲まれているので、ここでfalseならば処理自体がスキップされます。
left 0 < right 5 と、rightの方が大きいので
そのまま処理に入る
中央値のインデックスを (0+5)/2 で
2として
そのまま 再帰的に前半部のマージソートを呼び出し、繰り返していくと、
__mergeSort(a,0,2) → __mergeSort(a,0,1) → __mergeSort(a,0,0)となり
ここで初めて処理がスキップされるので、 __mergeSrot(a,0,1)から見ていきましょう、
※ a配列自体の変化なく、{6,5,4,3,2,1}のままです。
■ __mergeSort(a,0,1)の場合
後半部分のマージソートでは、__mergeSort(a,1,1)となりますが、
ここでも、
left 1 < right 1 はfalseなのでこのまま、①(aの前半部分をbuffへコピー)へ移ります。
①に入る
centerは0で、leftも0なので
buff[0] = a[0]の「1」がそのまま代入され、buffは {6,0,0,0,0,0}となります。
そのまま
iはインクリメントされ、 1 <= 0 がfalseなのでこのまま②(buffとaの後半部分とのマージ)に移ります。
while( 1 <= 1 && 0 < 1)となるので、
もし、buff[0] が、a[1]以下であれば buff[j]を、でなければa[i]を a[0(left)]に代入するというながれ
buff[0]の6は a[1]の5より大きいので、、a[1]の5がそのままa[0]に代入されます。 2 <= 1 がfalseなので
ここで、aの配列は{5,5,4,3,2,1}となり、③(buffの残り要素をaにコピー)へ移ります。
while(0 < 1) となるので、
a[1] = buff[0] となり、5,6,4,3,2,1, ← となり、 1 < 1 はfalseなので、ここで処理は終わり、
__mergeSort(a,0,2)へと処理が移ります。
■ __mergeSort(a,0,2)の場合
center は (0+2)/2となり、後半部分のマージソートは(a,1+1,2)として、
(a,2,2)として呼ばれるが、if文で弾かれるので、(a,0,2)の流れでいくと、まずは①から
buff[0] = a[0]が代入され、buffは{5,0,0,0,0,0}
続いて[1] = a[1]となり、 buffは{5,6,0,0,0,0}ここで 2 <= 1 がfalseなので ②に移ります。
while(2 <= 2 && 0 < 2) なのでこのまま
buff[0]の「5」はa[2]の「4」よりも大きいので
a[0]に a[2]の「4」を代入し、 aの配列は{4,6,4,3,2,1,}となります
while(3 <= 2)の時点でfalseなのでこのまま③に移ります。
while(0 < 2)なので、
a[1] = buff[0] を代入 {4,5,4,3,2,1,}
a[2] = buff[1]を代入 {4,5,6,3,2,1,}
となり、2 < 2 がfalseなのでこのまま抜けることになり、
前半部分のマージソートである__mergeSort(a,0,2)が完了します。
ここが終了したら、__mergeSort(a,3,5)へと移り、
今度は同様に後半部分のマージソートへ移るという感じです。
このように、大元の配列をまずは前半部と後半部に分けて
分けた後の配列も同様に前半部と後半部に分けて。。ということを再帰的な呼び出しで実現しています。
なお、離れた要素の交換は行わないので、冒頭の通り、安定なアルゴリズムということになります。
学んだこと
- 「マージする」というのは、ソート済みの2つの配列をソートしながら合成することを指す。
- コード上でのマージは、作業用の配列に元の配列の前半部分代入していき、aの後半と比較しながらマージしていく流れ
- 再帰的に呼ぶことで、繰り返しを実現できる
マージソートにおけるマージをイメージできればあとはそれをひたすら繰り返していく
という流れは掴めましたが、実現のために再帰呼び出しが複数使われるとなかなか理解が難しくなりそうですね汗
引き続き頑張っていきます!
※記事内の画像はITをわかりやすく解説から拝借致しました。