クイックソートとは
前回の記事では、単純挿入ソートをアップグレードしたシェルソートについて学んでみましたが、
今回はその流れでクイックソートについて学んでみたいと思います!
その名の通り、広く一般的に使われる高速なアルゴリズムであることからクイックソートと呼ばれていますが、
ざっくり言うと、中間位置を定めてその前後のグループ分けでソートを繰り返すといったようなものです。。
シェルソートでは等間隔のグループでソートを繰り返し、できる限りソート済の状態に近い形に持っていきましたが、
クイックソートでは、枢軸と呼ばれるグループ分けの基準のようなものを設けて、その前後でソートを行います。
と言葉にしてもイメージしにくので、実際に流れでやっていきましょう!
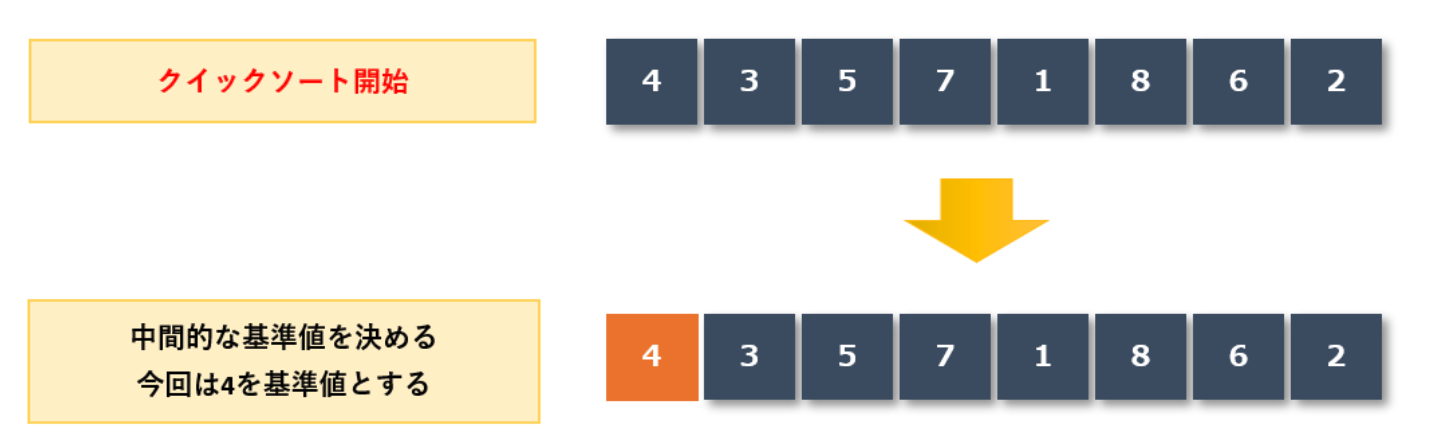
{4,3,5,7,1,8,6,2} という数列を昇順にソートしたいとして、
この内の中間的な値である「4」を枢軸として、その前後でグループ分けします。
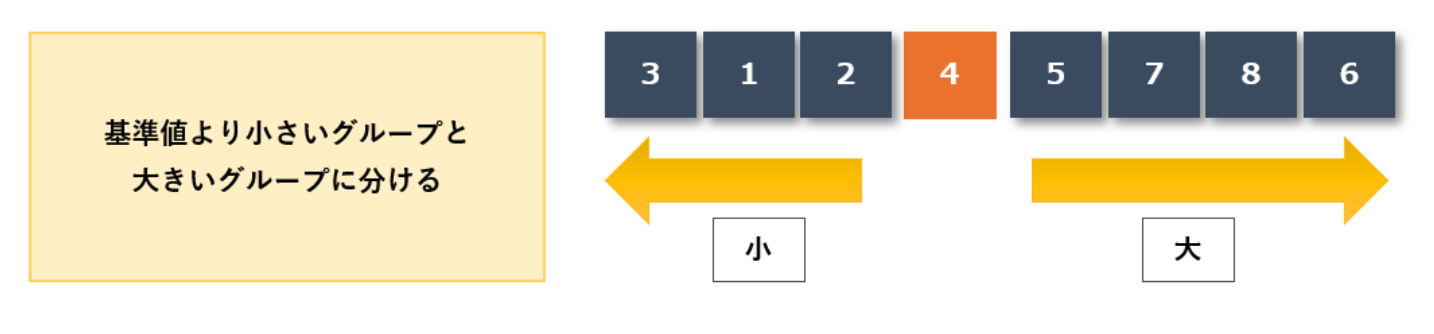
この「4」よりも大きいか小さいかでグループを二つに分けると、、
4よりも小さければ左に、大きければ右に寄せることで
4より小さいグループ:{3,1,2}
4より大きいグループ:{5,7,8,6} と分けることができました。
次に、小さいグループの中でも最初と同様に「2」を枢軸としてグループ分けします。

その「2」よりも大きいか小さいかでさらにグループ分けをすると、{1,2,3}という並びにすることができます
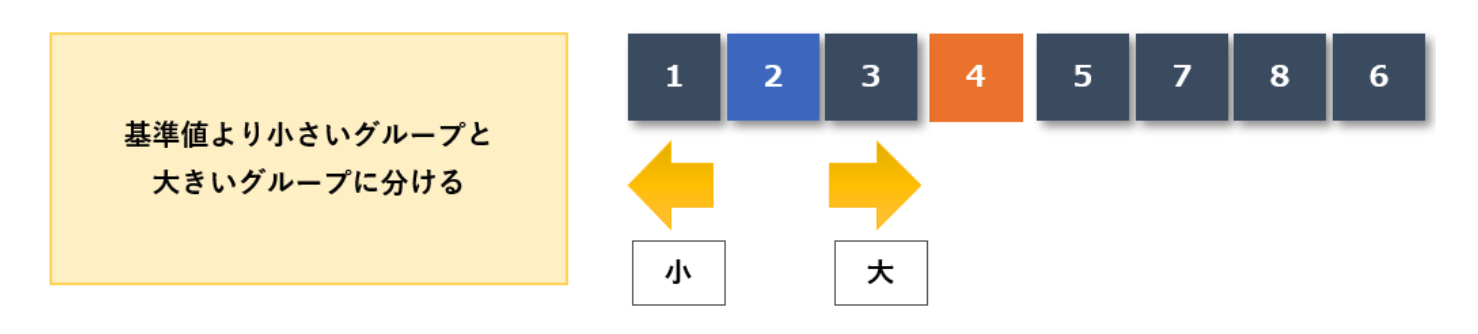
次に大きいグループも枢軸を「6」として同様のグループ分けを行います。

「6」よりも大きいか小さいかでさらにグループ分けすることで、{5,6,7,8}となりました。
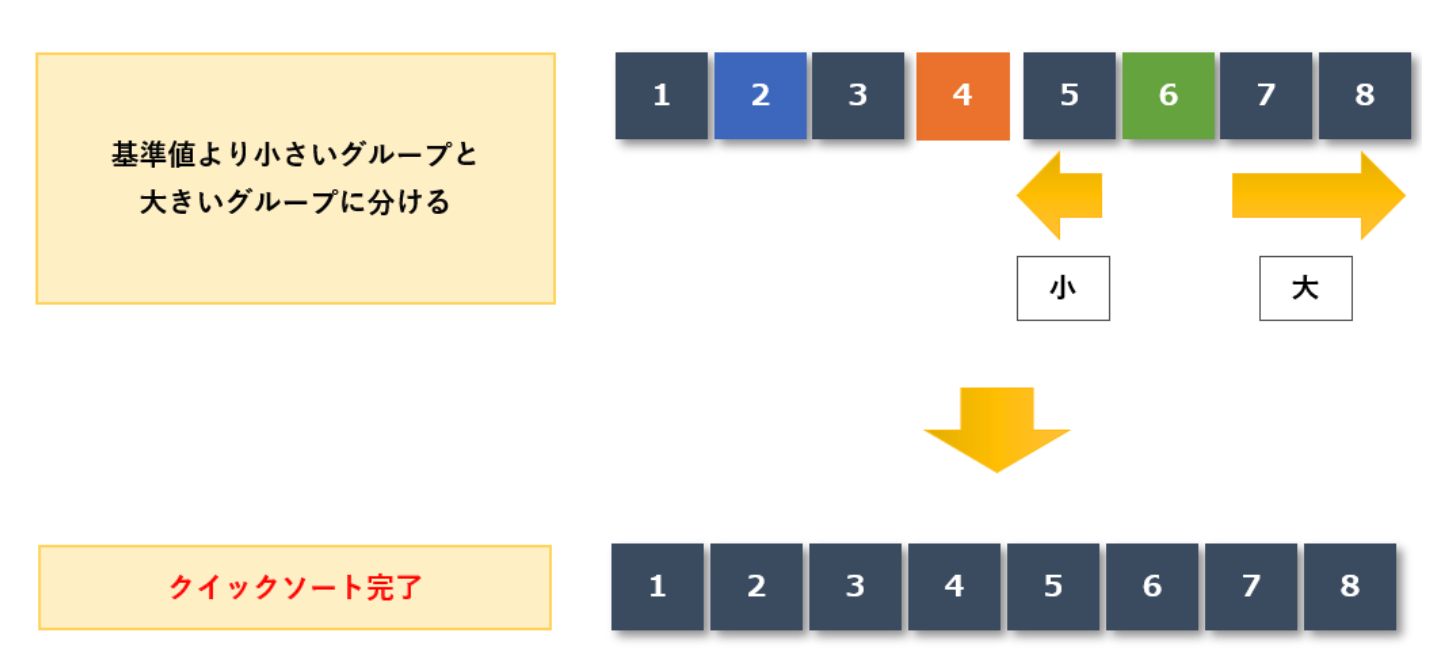
このように、枢軸よりも大きいグループ、小さいグループという分け方を続けることで
結果的に{1,2,3,4,5,6,7,8}とソートを完了させることができました。
これがクイックソートの流れですが、コードで表現するとなると、
分割の手順(枢軸を決めて大小でグループ分けを行う)をどう実現するかが肝になってきそうです。。
コードでどう表現するのか?
まずは分割する方法を考えていきたいところですが、基本的には下記2つの移動を実現させる必要がありそうです。
- 枢軸以下の要素を配列の左側(先頭寄り)に移動させる
- 枢軸以上の要素を配列の右側(末尾寄り)に移動させる
{5,7,1,4,6,2,3,9,8}という数列 aで考えてみると
枢軸をx とし、中央の「6]をxとします。
左端のインデックスをpl(左カーソル)
右端のインデックスをpr(右カーソル)としたとき、下記のように言い換えることができそうです。
- a[pl] >= xが成立する要素が見つかるまでplを右方向に走査する
- a[pr] <= xが成立する要素が見つかるまでprを左方向に走査する
左カーソルが x(枢軸)以上になるまで右方向に
右カーソルがx(枢軸)以下になるまで左方向に 走査する必要があるので、
{5,7,1,4,6,2,3,9,8}に上記の操作を行うと、下記の時点でストップします。
- plはa[2]である 「7」 >= 「6」でストップ
- prはa[6]である「3」 <= 「6」でストップ
左カーソルは枢軸以上の時、右カーソルは枢軸以下の時にストップするということですね。
ここで、左右のカーソルが位置する要素a[2]の「7」とa[6]の「3」の値を交換します。
すると、枢軸以下の値が左側に、枢軸以上の値が右側に移動するので、{5,3,1,4,6,2,7,9,8}となります
再び走査を続けると、左右のカーソルは
plはa[4]である「6」 >=「6」でストップ、prはa[5]である「2」<= 「6」でストップしますね。
左右のカーソル位置の値を交換すると、{5,3,1,4,2,6,7,9,8}
となり、
さらに走査を続けると、plとprは交差するのでこの時点で交換を終えると、カーソル位置は先ほどの交換の次にいくので、pl[5],pr[4]となります。
枢軸である「6」より小さいか、大きいかで以下のグループに分けることができました。
{5,3,1,4,2}と{7,8,9}
枢軸以下のグループ a[0]…a[pl-1] 先頭インデックス~左カーソルの手前まで
枢軸以上のグループa[pr+1]… a[n-1] 右カーソルの次~末尾インデックス
というグループ分けを行うことができます。
また枢軸と一致するグループが生まれる場合もあり、
例えば、{1,8,7,4,5,2,6,3,9}という数列で 「5」を枢軸にしたとすると、
plはa[1]である 「8」 >= 「5」でストップ
prはa[7]である「3」 <= 「5」でストップ → 交換を行い {1,3,7,4,5,2,6,8,9}
plはa[2]である 「7」 >= 「5」でストップ
prはa[5]である「2」 <= 「5」でストップ → 交換を行い {1,3,2,4,5,7,6,8,9}
plはa[4]である 「5」 >= 「5」でストップ
prはa[4]である「5」 <= 「5」でストップ → 交換を行い {1,3,2,4,5,7,6,8,9}となります
3回目の走査では、左右のカーソルが両方とも「5」でストップしており、
枢軸と一致する中央グループが登場することがわかります。 (分割完了時に、pl > pr + 1が成立するときのみ)
この分割過程をコードに落とし込んでみましょう。
static void partition(int[] a, int n) {
int pl = 0; // 左カーソル
int pr = n - 1; // 右カーソル
int x = a[n / 2]; // 枢軸(中央の要素)
do {
while (a[pl] < x) pl++; //左カーソルが枢軸未満の場合はplのインデックスを右に
while (a[pr] > x) pr--; //右カーソルが枢軸より大きい場合はplのインデックスを左に
//右カーソルが左カーソル以上の(交差してなければそのまま交換を行う)
if (pl <= pr){
swap(a, pl++, pr--);
}
} while (pl <= pr); //交差するまで(グループ分けが完了する)繰り返す
枢軸の値は配列の中央に位置する値ということにして、
do-while文で分割を繰り返しています。
a[pl]左カーソルが枢軸未満まで plのインデックスを インクリメントして右に移動
a[pr]右カーソルが枢軸より大きくなるまで prのインデックスをデクリメントして左に移動という流れです。
先ほどの{1,8,7,4,5,2,6,3,9}であれば、
plは0から、prは9-1 で8から始まり、xはa[9/2]なので、5とします。
while(a[0] < 5) の間は plをインクリメントするので
a[0]「1」 < 5 → a[1]「8」 < 5 でfalseなので pl は1となる
while(a[8] > 5)の間はデクリメントするので、
a[8]「9」> 5 →a[7]「3」> 5 で falseなので pr は7となる
if(1 <= 7)で交差はしていないので、
swap(a,1,7)で「8」「3」 の交換を行い、 {1,3,7,4,5,2,6,8,9}となります。
そのまま繰り返し処理の冒頭に戻りますが、
swapメソッドの引数でplは後置インクリメント、prは後置デクリメントしているので
plは 2 、prは6から始まります。
while(a[2] < 5) の間は plをインクリメントするので
a[2]「7」 < 5 → でfalseなので pl は2となる
while(a[6] > 5)の間はデクリメントするので、
a[6]「6」> 5 → a[5]「2」 > 5でfalseなのでplは5となる
if(2 <= 5)で交差はしていないので、
swap(a,2,5)で「7」「2」 の交換を行い、 {1,3,2,4,5,7,6,8,9}となります。
といったように、先ほどは文章で表した分割の流れをコードで再現することができました!
さらに、この配列分割を発展させてクイックソートを実現していきましょう。。!
コードに落とし込んでみる
先ほどの分割コードで、枢軸よりも大きいグループ、小さいグループで2つに分けることができましたが、
この分割後のグループにも最初の分割と同じ手続きを踏ませることで、クイックソートを実現できそうです。
static void quickSort(int[] a, int left, int right) {
int pl = left; // 左カーソル
int pr = right; // 右カーソル
int x = a[(pl + pr) / 2]; // 枢軸(中央の要素)
do {
while (a[pl] < x) pl++;
while (a[pr] > x) pr--;
if (pl <= pr)
swap(a, pl++, pr--);
} while (pl <= pr);
if (left < pr) quickSort(a, left, pr);
if (pl < right) quickSort(a, pl, right);
}
もし
要素数が1つしかないグループは、それ以上の分割は不要なので、
再分割を適用するのは要素数が2以上のグループとしたとき、
prが先頭より右側に位置する状態(left < pr)であれば、leftからprまでのグループで再度ソート
plが末尾より左側に位置する状態(pl < right)であれば、plからrightまでのグループで再度ソート
つまり、prが先頭まで、plが末尾まで来た場合それ以上は分割する必要がないということになります。
これを繰り返し行うので、再帰呼び出しで実現させることができるということですね!
{5,8,4,2,6,1,3,9,7}で実際にの処理過程を見てみましょう。
最初の呼び出しては quickSort(配列、0,8)
として、左端が0、右端が8というインデックスが渡されます
。
そのまま0が左カーソルのpl、8が右カーソルprとして、枢軸であるxはa[8/2]の6となります。
while(a[0] < 6) の間は plをインクリメントするので
a[0]「5」 < 6 → a[1]「8」 < 5 でfalseなので pl は1となります。
while(a[8] > 6)の間はprをデクリメントするので、
a[8]「7」> 6 →a[7]「9」> 6 → a[6] 「3」 > 6でfalseなので pr は6となります。
1 <= 6で交差はしていないので、そのままa[1]「8」,a[6]「3」を交換し
→{5,3,4,2,6,1,8,9,7}として
plが2prは5となり、 2 <= 5 はtrueなので、再度走査を続けます。
while(a[2] < 6) の間はplをインクリメントするので
a[2]「4」 < 6 → a[3]「2」 < 6 → a[4] 「6」 < 6 でfalseなのでplは4となります。
while(a[5] > 6)の間はprをデクリメントするので、
a[5]「1」> 6 で falseなのでprは5となります。
4 <= 5 で交差はしていないので、そのままa[4]「6」とa[5]「1」を交換し
→{5,3,4,2,1,6,8,9,7}
として、でplは5、prは4となり
5 <= 4 はfalseとなるので、while文を抜け、次のif文に移行します。
if (left < pr) で left 「0」 < 4 であれば再帰的に呼び出す
→ quickSort(a,0,4)で左グループのソート
if (pl < right) で 5 < right「8」であれば再帰的に呼び出す
→ quickSort(a, 5, 8)で右グループのソート
となるので、
左a[0] ~ a[4]{5,3,4,2,1}
右a[5] ~ a[8] {6,8,9,7}という2グループでそれぞれ同様の操作を行うことになる。
■{5,3,4,2,1}の場合
plは0 prは4で、枢軸は{5,3,4,2,1,6,8,9,7}
のa[(0 + 4)/2]である「4」となります。
while(a[0] < 4) の間は plをインクリメントするので
a[0]「5」 < 4 でfalseなのでplは0となります。
while(a[4] > 4)の間はデクリメントするので、
a[4]「1」> 4 でfalseなのでprは4のまま
0 <= 4で a[0]「5」 とa[4] 「1」を交換し、{1,3,4,2,5} そのまま plは1 pr は3となります。
while(a[1] < 4) の間は plをインクリメントするので
a[1]「3」 < 4 → a[2]「4」 < 4 でfalseなので pl は2ととなります。
while(a[3] > 4)の間はデクリメントするので、
a[3]「2」> 4 でfalseなのでprは3となり、
2 <= 3
で a[2]「4」とa[3]「2」を交換し {1,3,2,4,5}
plは3 pr は2となります。
while(a[3] < 4) の間は plをインクリメントするので
a[3]「4」 < 4 はfalseなので pl は3となります。
while(a[2] > 4)の間はデクリメントするので、
a[2]「2」> 4 はfalseなのでprは2となる
3 <= 2 はfalseとなるのでwhile文を抜け、次のif文に移行します。
if (left < pr) で left 「0」 < 2 であれば再帰的に呼び出す → quickSort(a,0,2)で左グループのソート
if (pl < right) で 3 < right「4」であれば再帰的に呼び出す → quickSort(a, 3, 4)で右グループのソートを
{5,3,4,2,1}から、左は{1,3,2}右は{4,5}とグループ分けされます。
■ {6,8,9,7}の場合
pl が5 prが8で、枢軸は{1,3,2,4,5,6,8,9,7}
のa[(5+8)/2]である「8」となります
while(a[5] < 8) の間は plをインクリメントするので
a[5]「6」 < 8 → a[6] 「8」< 6 falseなので pl は6となります。
while(a[8] > 8)の間はデクリメントするので、
a[8]「7」> 8 はfalseなのでprは8となります。
6 <= 8なので、そのままa[6]「8」とa[8]「7」を交換して{6,7,9,8}となり、plは 7 prは7 なので
while(a[7] < 8) の間は plをインクリメントするので
a[7]「9」 < 8 → falseなので pl は7となります。
while(a[7] > 8)の間はデクリメントするので、
a[7]「9」> 8 → a[6]「7」 > 8 でfalseなのでprは6となります。
7 <= 6ではないのでここでwhile文を抜け、次のif文に移行します。
if (left < pr) で left 「5」 < 6 であれば再帰的に呼び出す → quickSort(a,5,6)で左グループのソート
if (pl < right) で 7 < right「8」であれば再帰的に呼び出す → quickSort(a, 7, 8)で右グループのソートを
{6,7}{9,8}でそれぞれソートを行う。。という繰り返しを行うことで、クイックソートの手順を実現させることができそうです。
グループ分けをしてソートしているという表現になりますが、実際は常に配列aをquicksortに渡しているので、
着目する範囲のインデックスをそれぞれ前半と後半に分けてソートしているだけで、実際に分割しているわけではなさそうですね。。
ちなみに、クイックソートは隣接していない離れた要素を交換するので不安定という点には注意が必要です!
学んだこと
- 枢軸を選択し、その大小でソート範囲を決めていくので、ソートする範囲は常に近い値で2分されるためクイックなソートが可能
- 先頭、末尾からカーソルを動かすことで、大小のグループ分けを行える
- 配列を操作する上では、インデックスで着目範囲を決めれば分割という操作を実現することができる
使用機会が多いクイックソートですが、分割をどうやって表現するんだろう。。と悩みましたが
カーソルと、着目要素をずらしていき、再帰的に処理することで実現できスッキリできました!
インデックスを変えれば、事実上分割しているかのように処理できるので、この考え方は
今後も使っていきたいですね。。引き続き頑張っていきます!
※記事内の画像はITを分かりやすく解説から拝借しております。