NumpyのFFT入門(2) np.fft実習

Last updated at 2024-08-07Posted at 2024-08-04

NumPyのFFT機能

NumPyは、Pythonで科学技術計算を行うための強力なライブラリであり、FFTを実行するための多くの関数を提供しています。これにより、信号処理やデータ解析を簡単に行うことができます。ここでは、np.fftモジュールの基本的な機能を紹介します。

np.fftモジュールの概要

np.fftモジュールは、NumPyでFFTおよび逆FFTを行うための一連の関数を提供します。このモジュールを利用することで、複雑な信号を効率的に周波数領域に変換し、また時間領域に戻すことが可能です。主要な関数には、fft（FFTの計算）、ifft（逆FFT）、fftfreq（周波数成分の生成）、およびfftshift（周波数成分のシフト）が含まれます。

1. np.fft.fftとnp.fft.ifftの基本的な使い方

np.fft.fft

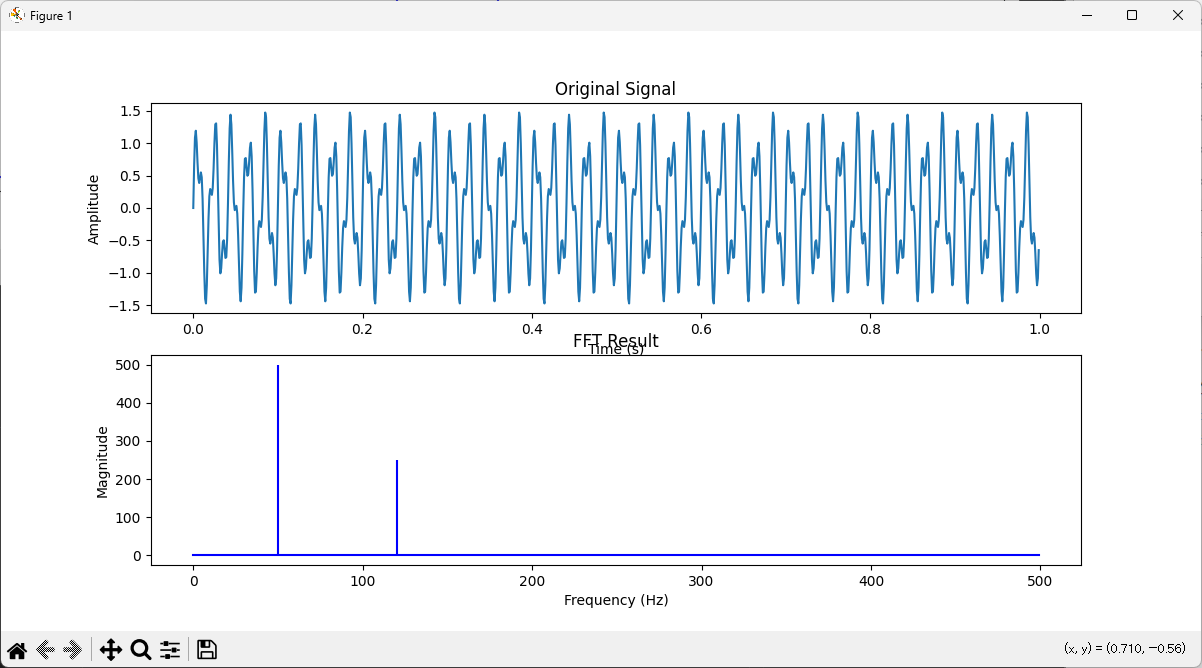
np.fft.fftは、時間領域の信号を周波数領域に変換するための関数です。FFTを計算することで、信号内の周波数成分の強度と位相を取得できます。

import numpy as np
import matplotlib.pyplot as plt

# サンプルデータの生成
sampling_rate = 1000  # サンプリング周波数（Hz）
T = 1.0 / sampling_rate  # サンプリング間隔
t = np.arange(0, 1.0, T)  # 時間ベクトル

# 信号生成（50Hzと120Hzのサイン波を重ねたもの）
f1 = 50  # Hz
f2 = 120  # Hz
signal = np.sin(2*np.pi*f1*t) + 0.5*np.sin(2*np.pi*f2*t)

# FFT実行
fft_result = np.fft.fft(signal)

# 周波数軸の計算
freqs = np.fft.fftfreq(len(signal), T)

# FFT結果のプロット
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(t, signal)
plt.title('Original Signal')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')

plt.subplot(2, 1, 2)
plt.stem(freqs[:len(freqs)//2], np.abs(fft_result)[:len(freqs)//2], 'b', markerfmt=" ", basefmt="-b")
plt.title('FFT Result')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.tight_layout()
plt.show()

コードの解説

FFT実行

fft_result = np.fft.fft(signal)

np.fft.fft(signal):
- np.fft.fft()はNumPyライブラリの関数で、**離散フーリエ変換（DFT）**を計算します。
- 引数:
  - signal: FFTを適用する対象の信号データです。この信号は時間領域のデータであり、FFTを適用することで周波数領域のデータに変換されます。
- 戻り値:
  - fft_result: 周波数領域での複素数の配列。振幅と位相情報を含みます。np.abs(fft_result)で振幅を、np.angle(fft_result)で位相を取得できます。

周波数軸の計算

freqs = np.fft.fftfreq(len(signal), T)

np.fft.fftfreq(n, d=1.0):
- np.fft.fftfreq()は、FFT結果に対応する周波数の配列を生成します。
- 引数:
  - n: 信号のデータ点の数。この場合、len(signal)が渡され、信号のサンプル数（データ点の総数）を指定しています。
  - d: サンプリング間隔（秒）。ここではTが渡されており、1秒あたりのサンプリング数に基づくサンプリング時間です。Tは1.0 / sampling_rateで計算され、サンプリング周波数の逆数です。
- 戻り値:
  - freqs: FFTの結果に対応する周波数の配列。この配列は正負の周波数を含み、信号の周期性を表す周波数成分を示しています。

全体の流れ

サンプルデータの生成:
- サンプリング周波数1000 Hzで、1秒間の時間ベクトルtを生成し、50Hzと120Hzのサイン波を重ねた信号signalを作成します。
FFTの実行:
- np.fft.fft()を使って、時間領域の信号を周波数領域に変換し、その結果をfft_resultに格納します。
周波数軸の計算:
- np.fft.fftfreq()を用いて、FFT結果に対応する周波数の配列freqsを計算します。
プロット:
- 元の信号とFFT結果の振幅スペクトルをプロットして、時間領域と周波数領域での信号の特性を視覚的に確認します。

このようにして、元の信号の周波数成分を明らかにすることができ、例えば信号中に存在する特定の周波数成分（この例では50Hzと120Hz）が確認できます。

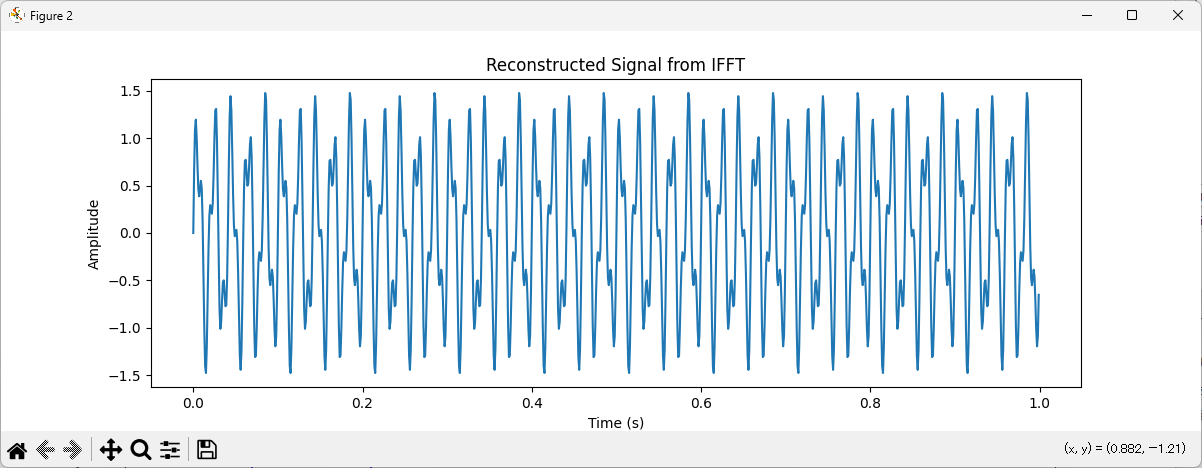
np.fft.ifft

np.fft.ifftは、周波数領域のデータを時間領域に逆変換するための関数です。これにより、FFT後に処理した信号を元の時間領域信号に戻すことができます。

# 逆FFT実行
ifft_result = np.fft.ifft(fft_result)

# 元の信号と再構築信号の比較
plt.figure(figsize=(12, 4))
plt.plot(t, ifft_result.real)
plt.title('Reconstructed Signal from IFFT')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.show()

以下では、逆フーリエ変換（Inverse Fast Fourier Transform, IFFT）を実行する部分について解説します。

逆FFT実行

ifft_result = np.fft.ifft(fft_result)

np.fft.ifft(fft_result):
- np.fft.ifft()はNumPyライブラリの関数で、**逆離散フーリエ変換（IDFT）**を計算します。FFTによって周波数領域に変換されたデータを、再び時間領域に戻すために使用します。
- 引数:
  - fft_result: 逆FFTを適用する対象の周波数領域のデータ。このデータはnp.fft.fft()を用いて取得されたもので、周波数領域の複素数配列です。
- 戻り値:
  - ifft_result: 時間領域の信号に戻った複素数の配列。この配列はもとの時間領域信号を復元したもので、理想的には元の信号signalと同じです。ただし、数値計算誤差のため、小さな虚数成分が含まれることがあります。

全体の流れにおける役割

信号の周波数領域への変換:
- np.fft.fft()を使用して、時間領域の信号を周波数領域に変換します。この変換により、信号中の周波数成分を解析することができます。
周波数領域からの信号復元:
- np.fft.ifft()を使用して、周波数領域で得られたデータを再び時間領域に戻します。このプロセスは、周波数領域で行った操作（例：フィルタリングや圧縮）を逆に適用し、元の信号を再構築するために重要です。

数値例

例えば、元の信号signalが
$$ \text{signal}(t) = \sin(2\pi \times 50 , t) + 0.5 \sin(2\pi \times 120 , t) $$
であるとき、FFTを行うと、周波数領域でのスペクトルが得られます。これに対して逆FFTを適用することで、元の時間領域信号に近い形に戻すことができます。

注意点

数値誤差: IFFTを適用した結果には、計算上の小さな誤差が生じることがあります。この誤差により、出力が完全に実数にはならず、わずかな虚数成分が現れることがあります。この場合、ifft_result.realを用いて実数部を抽出することが一般的です。
信号処理の目的: IFFTは、信号処理において周波数領域での操作を反映させた信号を再構築する際に不可欠です。例えば、ノイズを除去したり、特定の周波数を強調したりするための操作を周波数領域で行い、その後にIFFTを適用することで、処理結果を時間領域で確認できます。

2.np.fft.fftfreqとnp.fft.fftshiftの活用

np.fft.fftfreq

np.fft.fftfreqは、FFTの結果に対応する周波数成分を計算するための関数です。サンプル数とサンプリング間隔を指定することで、各周波数成分の値を取得できます。

# 周波数成分の計算
freqs = np.fft.fftfreq(len(signal), T)

# 計算された周波数の表示
print(freqs[:10])  # 最初の10個の周波数成分を表示

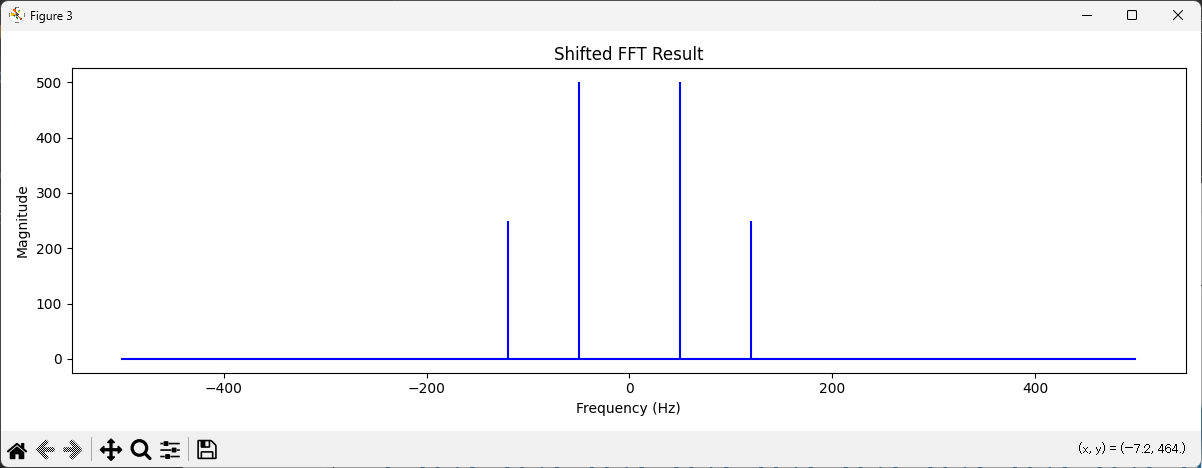
np.fft.fftshift

np.fft.fftshiftは、周波数成分をゼロ周波数成分を中心にシフトするための関数です。これにより、周波数の対称性を可視化しやすくなります。

# FFTのシフト
shifted_fft = np.fft.fftshift(fft_result)
shifted_freqs = np.fft.fftshift(freqs)

# シフト後のFFT結果のプロット
plt.figure(figsize=(12, 4))
plt.stem(shifted_freqs, np.abs(shifted_fft), 'b', markerfmt=" ", basefmt="-b")
plt.title('Shifted FFT Result')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.show()

そもそもnp.fft.fftshiftが使われる理由

np.fft.fftshiftは、FFT（高速フーリエ変換）を行った後に得られる周波数スペクトルを見やすくするために使用される関数です。これが必要とされる理由を、以下のポイントを中心に解説します。

周波数スペクトルの対称性

FFTの出力:
- FFTを適用すると、出力は周波数成分の配列として得られます。この配列は、通常、0 HzからNyquist周波数までの正の周波数成分が前半に、-Nyquist周波数から0 Hzまでの負の周波数成分が後半に配置されています。
- 具体的には、FFTの出力は通常、以下のように並びます：
  - [0, f1, f2, ..., fN/2, -fN/2, ..., -f2, -f1]
可視化の問題:
- この出力のままでは、周波数スペクトルの可視化が直感的ではありません。通常、ユーザーは周波数軸が中央（0 Hz）から左右対称に広がる形を好みます。
- 中央に0 Hzを配置し、その左右に負と正の周波数成分を配置することで、信号の周波数特性を視覚的に把握しやすくなります。

np.fft.fftshiftの役割

役割:
- np.fft.fftshiftは、FFTの結果として得られた周波数配列を再配置して、周波数成分を0 Hzを中心に並べ替えます。
- 具体的には、前半の正の周波数成分と後半の負の周波数成分を入れ替えます。
効果:
- 配列をシフトすることで、スペクトルが以下のように配置されます：
  - [-fN/2, ..., -f2, -f1, 0, f1, f2, ..., fN/2]
- これにより、スペクトルをプロットした際に、0 Hzがグラフの中央に位置し、その左右に対称的に負と正の周波数が広がるため、視覚的に理解しやすくなります。

np.fft.fftshift結論

np.fft.fftshiftを用いることで、周波数スペクトルの中央に0 Hzを配置し、その左右に対称的に周波数成分を配置できるため、周波数特性の分析や可視化が容易になります。
特に、信号処理やスペクトル解析の際に、信号の対称性や特性を直感的に理解しやすくするために有用です。

まとめ

以下にNumPyのFFT関数の使用例とその効果を整理します。

関数	目的	使用例	効果
`np.fft.fft`	時間領域を周波数領域に変換	`fft_result = np.fft.fft(signal)`	信号の周波数成分を取得
`np.fft.ifft`	周波数領域を時間領域に逆変換	`ifft_result = np.fft.ifft(fft_result)`	周波数領域での操作を時間領域に戻す
`np.fft.fftfreq`	周波数成分を計算	`freqs = np.fft.fftfreq(len(signal), T)`	各周波数成分に対応する周波数を取得
`np.fft.fftshift`	周波数成分をゼロ周波数を中心にシフト	`shifted_fft = np.fft.fftshift(fft_result)`	周波数の対称性を可視化しやすくする