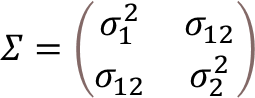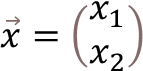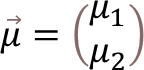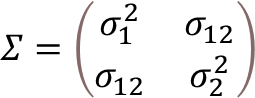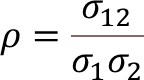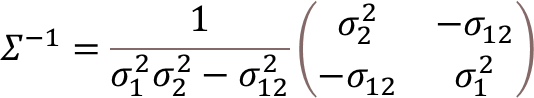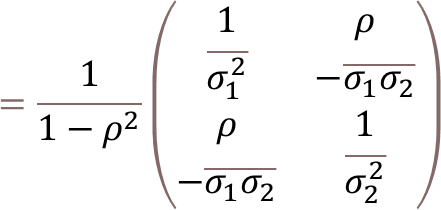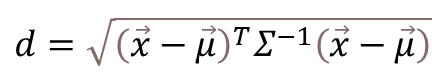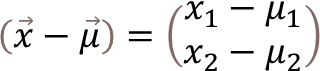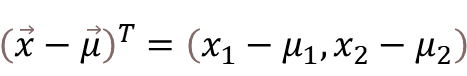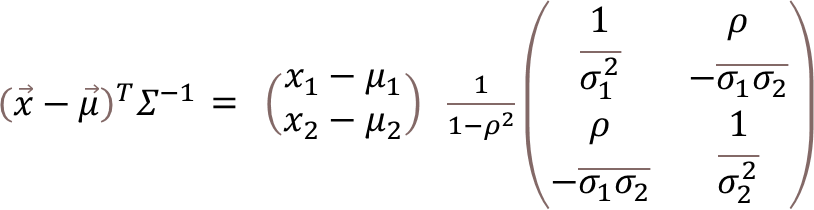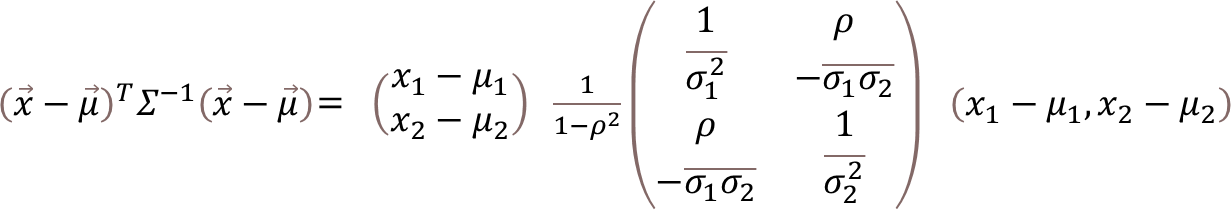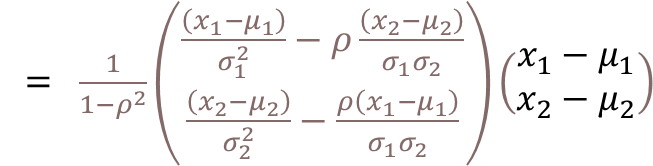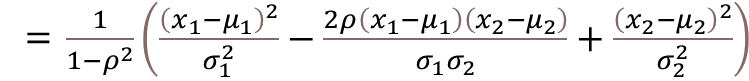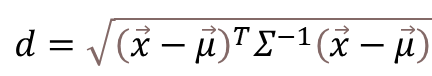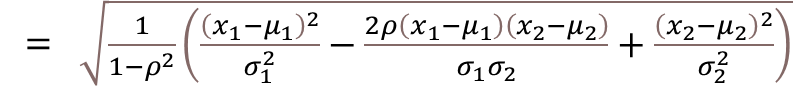#1. はじめに
先日、井手剛さんのTwitterで注目すべき発言がありました。異常検知においてSOTAは、マハラノビス距離であるとの報告でした。素晴らしいと思いました。
＊井手剛さんは、名著入門機械学習による異常検知の著者です。
ということで、統計を専門的に学んでない方を対象に、このマハラノビス距離を嚙み砕いて説明したいと思います。
#2.マハラノビス距離とは
##2.1. マハラノビス先生
最初、マハラノビス先生について、お話させてください。活動時期がラマヌジャンと似ていて、なんだかインド生まれの変わった風貌を持つ天才数学者のイメージがありましたが、実写の写真を見るとかなりインテリのイメージでした。彼の功績を見ると、天才数学者であることは間違いありませんが。ケンブリッジ大学に留学した後、インドのコルカタに戻り、インド統計研究所(Indian Statistical Institute)で数理統計学の研究を続けました。
マハラノビス距離については、1936年のProceedings of the National Institute of Sciences of Indiaに“On the generalized distance in statistics”のタイトルでその概念を発表しました。他の数学天才の論文と違い、ちゃんと数式を展開しながら内容も説明してくれるので、理解しやすい論文ですので、ご興味のある方は直接に読んでみてください。個人的には、このGeneralized Distanceのタイトルにマハラノビス先生の自信が見えてました。汎用的な、あらゆる分野で適用できる素晴らしい距離の概念である。という先生の主張が「Generalized」という言葉に現れたと感じました。
##2.2. マハラノビス距離
マハラノビス距離とは、多変数間の相関関係を取り入れて、既知のサンプルとの関係を明らかにする距離です。
(1) 多変数の意味は、1変数を含めた多変数を取り扱う問題に使える
(2) そして、その多変数間の相関関係を考慮した内容
(3) 既知のサンプルとの関係は、例えば品質管理において良品のデータの分布を持っている場合、それを基準に異常検知に使える基準が作れることを意味します。
よく使われるユークリッド距離とマハラノビス距離の違いを説明する図を下記に示します。
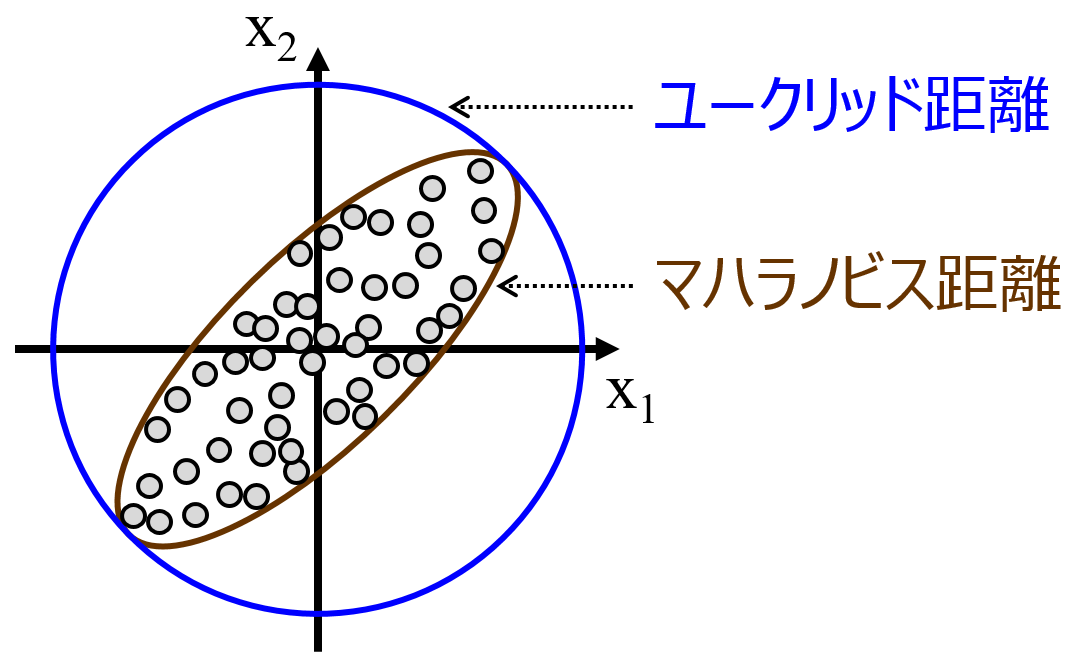
"出典：金子研究室HP＠明治大学"
#3.数式の理解
マハラノビス距離dは下記の式で定義されます。
各記号の意味はこちらになります。
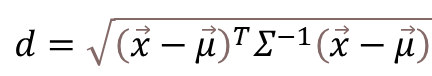
ここで、注目して頂きたいのは、𝛴と表記される分散・共分散行列です。英語のVariance-Covariance Matrixを直訳した言葉で、𝛴と書かれたため、合計の演算子と読み間違えらえることがありますが、中身は行列式になります。
例えば、X1,X2の2次元のデータがあるとき、このデータの分散・共分散行列は下記のように表記されます。
データが3次元の場合は、下記のようになります。
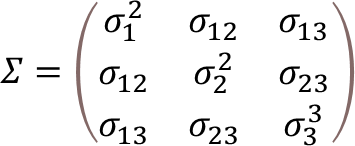
𝛴=(■(𝜎_1^2&𝜎_12&𝜎_13@𝜎_12&𝜎_2^2&𝜎_23@𝜎_13&𝜎_23&𝜎_3^3 ))
#3.1. 2次元のマハラノビス距離
ここでは、X1,X2の2次元のデータがあるとき、マハラノビス距離dの数式を解いてみたいと思います。簡単な計算でありながら、案外もその過程が説明されてなかったため、ここでご説明することにします。
まず、データのベクトルです。
次に平均のベクトルです。
分散・共分散行列です。これは前章で説明した通りです。
ここで、相関係数を下記の式のようにすると、
分散・共分散行列の逆行列を下記に表記することができる。
ここで、マハラノビス距離の式に代入する。
マハラノビス距離のルートの中の式を完成していきます。
従って、マハラノビス距離のdは、下記の式のようにスカラーになることが分かる。
#4. 次回の予定
Pythonで多次元データからマハラノビス距離を求め方を説明します。
#5. 参考資料