# 画像処理 エッジ&コーナー検出のための空間フィルタリング(2)

本記事では、前回投稿した記事の続きでノンローカルミーンフィルタについて記していきます。

前回記事はこちらです。

ノンローカルミーンフィルタとは

ノンローカルミーンフィルタの考え方としては、注目する画素の周辺と、他の画素の周辺の類似度を調べ、類似度が高ければ重み付けを大きくし、逆に低ければ重み付けを小さくするという考え方になっています。

このフィルタリングを用いることで、残すべき輪郭を残しながらノイズの平滑化を行えるようになっています。

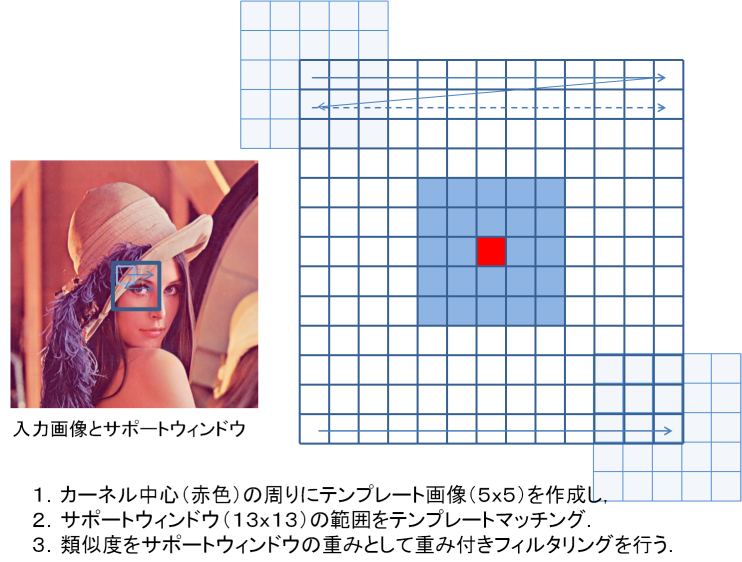
この写真は、こちらの「OpenCV」のホームページから引用させていただきました。

そのため、カーネルの大きさ(上記画像の大きい枠(13×13))と、比較する周辺範囲の大きさ(上記画像の小さい枠(5×5))の2つを決めてフィルタリングを行いますので、この2つの大きさをあらかじめ定める必要があります。

ノンローカルミーンフィルタの理論

注目する画素$p$に対する周辺画素$q$の重みを$w(p, q)$とするとき、重み$w(p, q)$は以下の式で表されます。

\begin{align}
w(p, q) &= \frac{1}{Z(p)}\exp\Biggl(-\frac{\max\bigl(||v(p) - v(q)||^2 - 2\sigma^2, 0\bigr)}{h^2}\Biggr)\\
Z(p) &= \sum_{q\in S}\exp\Biggl(-\frac{\max\bigl(||v(p) - v(q)||^2 - 2\sigma^2, 0\bigr)}{h^2}\Biggr)
\end{align}

$Z(p)$は規格化するためにカーネルの総和で割るために計算をしています。
また、$v(p)$と$v(q)$はそれぞれ注目している画素とその周辺の画素の画素値の情報です。
その差分についてノルム計算を行うことによって類似度を計算します。ノルム計算結果が小さいほど類似度が高いと判断できます。

また、パラメータとして$\sigma$と$h$の2つを調整する必要があります。

$\sigma$はノイズの分散の値になるように調整すると良いとされております。
また、$h$は画素比較の敏感さを表しております。値が大きくなるほど違いに対して鈍感(値の違いが大きくても似ていると判断)になり、逆に小さくなるほど敏感(値の違いが少しでも異なると違うものとして判断)するようになります。
この2つのパラメータは、画像ごとに適宜調整していく必要があります。

Pythonでの実装

import numpy as np
import cv2

# カーネル関数
def kernel_function(v_p, v_q, sigma, h):
    # 配列を一次元化
    v_p, v_q = v_p.flatten(), v_q.flatten()
    # ノルム計算
    v = (np.sqrt(np.sum((v_p - v_q) ** 2))) - 2 * (sigma ** 2)
    # 0より大きいかどうかを比較
    v_max = v if v > 0 else 0
    return np.exp(-(v_max / (h ** 2)))

# カーネルを作成する関数
def create_kernel(window, matrix, sigma, h, kernel_size):
    kernel = np.zeros((kernel_size))
    matrix_shape = matrix.shape
    for x in range(kernel_size[1]):
        for y in range(kernel_size[0]):
            template = window[y: y + matrix_shape[0], x: x + matrix_shape[1]]
            kernel[y][x] = kernel_function(template, matrix, sigma, h)
    kernel_norm = kernel / np.sum(kernel)
    return kernel_norm

# ノンローカルミーンフィルタ
def non_local_means_filter(img, template_size=(5, 5), kernel_size=(13, 13), sigma=1, h=1):

    # フィルタをかける画像の高さと幅を取得
    height, width = img.shape

    # カーネル作成に必要な範囲を計算
    require_height, require_width = template_size[0] + int(kernel_size[0]- 1), template_size[1] + int(kernel_size[1]- 1)

    # それぞれの幅を計算
    height_ignore, width_ignore = int((require_height - 1) / 2), int((require_width - 1) / 2)
    template_range = (int((template_size[0] - 1) / 2), int((template_size[1] - 1) / 2))
    kernel_range = (int((kernel_size[0] - 1) / 2), int((kernel_size[1] - 1) / 2))

    # 出力画像用の配列
    img_filter = img.copy()

    # フィルタリングの計算
    for y in range(height_ignore, height - height_ignore):
        for x in range(width_ignore, width - width_ignore):
            # カーネルを作成
            window = img[y - height_ignore: y + height_ignore + 1, x - width_ignore: x + width_ignore + 1]
            matrix = img[y - template_range[0]: y + template_range[0] + 1, x - template_range[1]: x + template_range[1] + 1]
            kernel = create_kernel(window, matrix, sigma, h, kernel_size)
            # カーネルを用いて計算
            calculate_kernel = img[y - kernel_range[0]: y + kernel_range[0] + 1, x - kernel_range[1]: x + kernel_range[1] + 1]
            img_filter[y][x] = np.sum(calculate_kernel * kernel)
    return img_filter

少しごちゃごちゃしていますが、自分なりに数式を再現した結果がこのソースコードになりました。

これらの関数を用いてフィルタリングを行います。

# 入力画像を読み込み
img_gray = cv2.imread("/ml_directory/dl/filter/rankuru_noise.jpg", cv2.IMREAD_GRAYSCALE)
img_filter = non_local_means_filter(img_gray, template_size=(5, 5), kernel_size=(13, 13), sigma=2.7, h=2.7)

import matplotlib.pyplot as plt
fig, (ax1, ax2) = plt.subplots(nrows=2, ncols=1, figsize=(20, 30))
ax1.imshow(img_gray, cmap='gray')
ax2.imshow(img_filter, cmap='gray')
ax1.set_xticks([]); ax1.set_yticks([])
ax2.set_xticks([]); ax2.set_yticks([])
plt.show()

実行結果は以下のようになりました。

バイラテラルフィルタの時と同様、輪郭をしっかり残した状態でフィルタリングができていることがわかります。
(OpenCVのライブラリより精度が劣った結果となってしまっていますが...)

計算量が他のフィルタに比べ増加しているため、実行にはかなり時間を要してしまう問題点があります。
また、OpenCVのノンローカルミーンフィルタでは、$\sigma$と$h$のパラメータをノイズ推論を用いて最適になるように調整する設計となっているようです。
このソースコードは推論する機能はないので最適解を実験を通して調べていきましたが、調整がかなりシビアになってしまう問題があります。

まとめ

本記事では、前回のガウシアンフィルタとバイラテラルフィルタに続き、ノンローカルミーンフィルタについて理論について勉強し、そしてPythonで自力実装をしてみました。

これはあくまで機械学習でいう前処理的な立ち位置ですので、次回以降では、このフィルタを応用したエッジ検出などについて書いていこうと思います。

以上となります。