前置き
本記事はfreeeデータに関わる人たち Advent Calendar 2020におけるDay 8のエントリーです。
目的
いくつかの有名な統計分布について、計算機実験で再現することで「わかったつもり」から「腑に落ちた状態」を目指します。
自分で数理モデルを組む際に、仮定する分布まで気を使える繊細さを身に着けたい(願望)
ここで扱う統計分布は以下の通り。いずれもベーシックな教科書に出てくるもので、統計学入門を参考にしつつ、主に待ち時間分布として知られる分布群にフォーカスします。
- 正規分布
- 指数分布
- ガンマ分布
- ワイブル分布
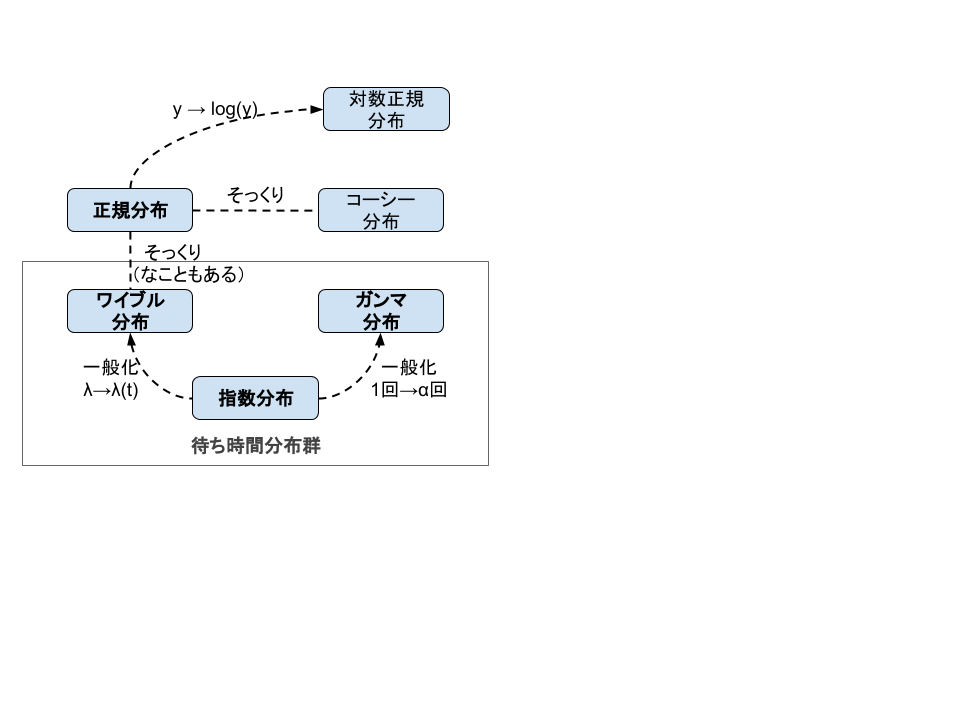
扱う統計分布とその関係性
計算機実験で分布を再現する前に、今回対象にしたそれぞれの分布の関係性を図に落としてみます。
ここでは納得感を優先してザクッとした限定的な関連で描くので、一般性や網羅性には欠けてても気にしないことにします
正規分布周辺はおまけで書いてますが、今回はほぼ対象外です。
待ち時間分布として知られる指数分布と、その一般化分布であるガンマ分布、ワイブル分布が今回の主なターゲットです。一般化の方向が異なるのがおもしろポイント。
特に発生確率に時間依存性入れたものに対応するワイブル分布は、工学的な応用と対応づけることができてかなり興味深い分布といえます。
計算機実験で再現してみる
正規分布
理論化学〜物理バックグラウンドを持つ僕はGauss分布と呼びたくなる超有名分布。最近やっと自然と正規分布って言えるようになりました。
$\mu, \sigma$を平均、標準偏差とすると、密度関数は以下で表されます。
f(x) = \frac{1}{\sqrt{2\pi\sigma}}\exp\left(\frac{-(x-\mu)^2}{2\sigma^2}\right)
測定誤差分布や生物測定の分野によく見いだされる分布。他にも正規分布はランダムな系列の和や平均としても生じ、中心極限定理へとつながっています。
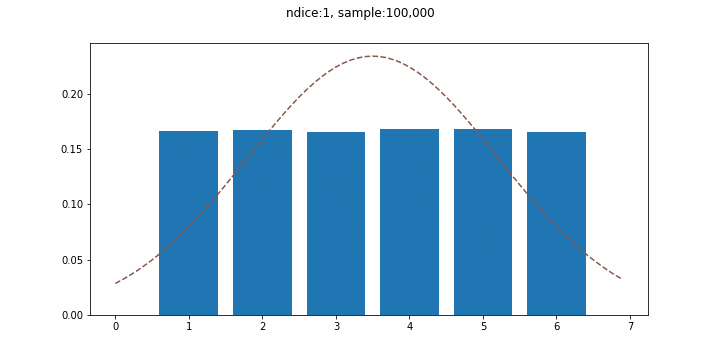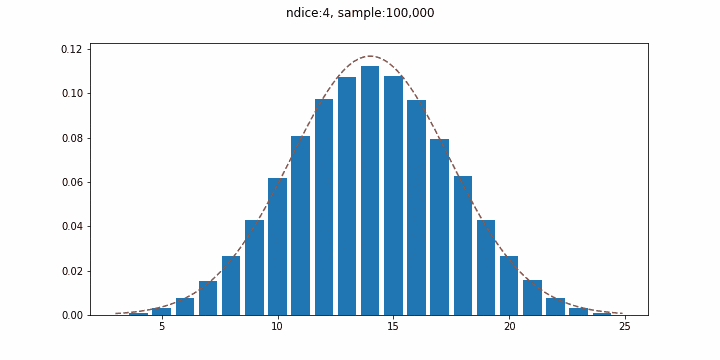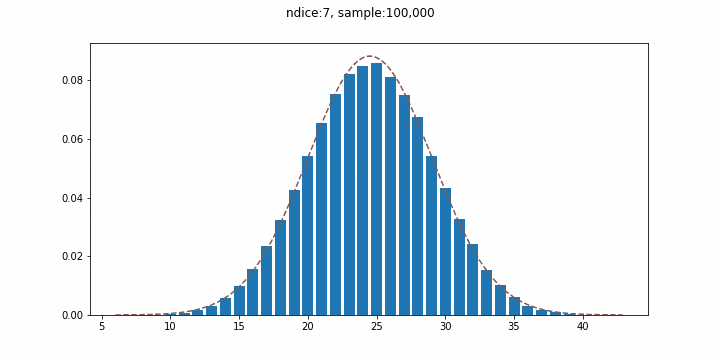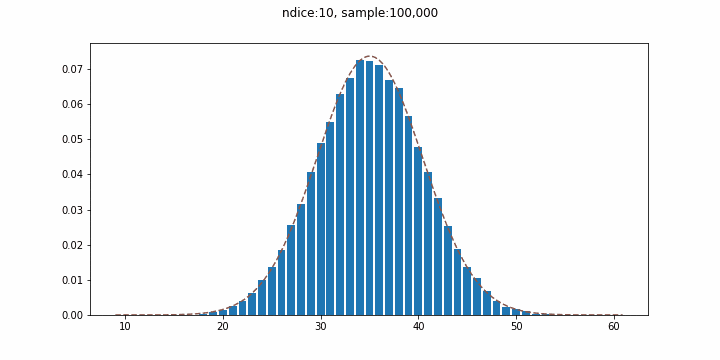
ここでは、$n_{dice}$個のサイコロを振った際の目の和の分布として正規分布を再現し、段々とサイコロの数を増やしてみることにします。点線は実際の正規分布を表し、棒グラフが概ね近似的な正規分布となっていることが確認できます。
指数分布
指数の肩に負の一次関数を載せたものは単調減少の確率分布として成立します。
$\lambda$を正の数として、密度関数は以下。
f(x) = \lambda \exp\left(-\lambda x\right)
平均、分散はそれぞれ $\lambda ^{-1}, \lambda ^{-2}$で表され、$x\geq 0$の範囲でのみ定義されます。
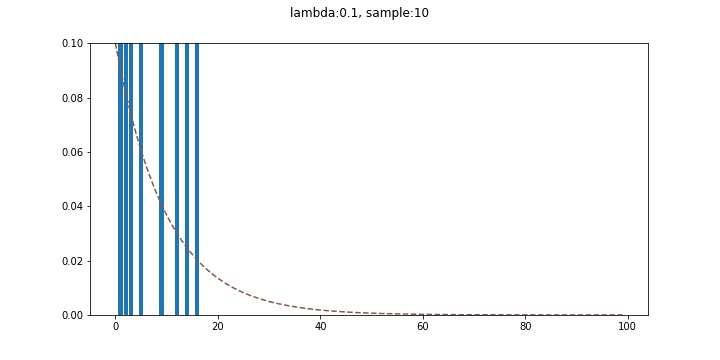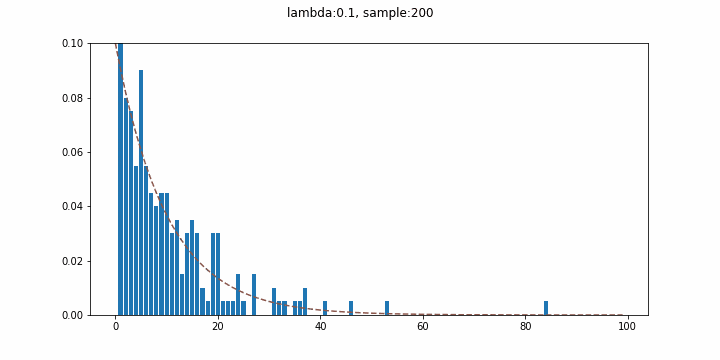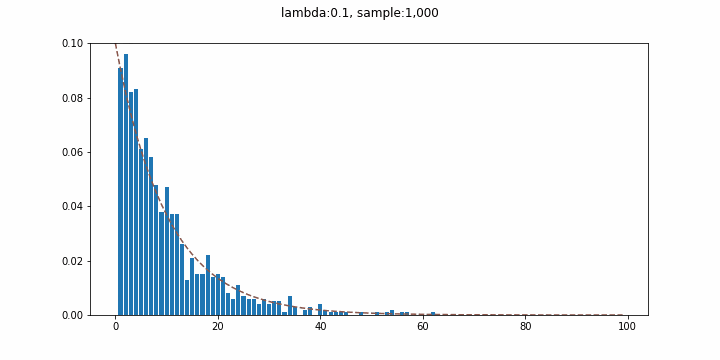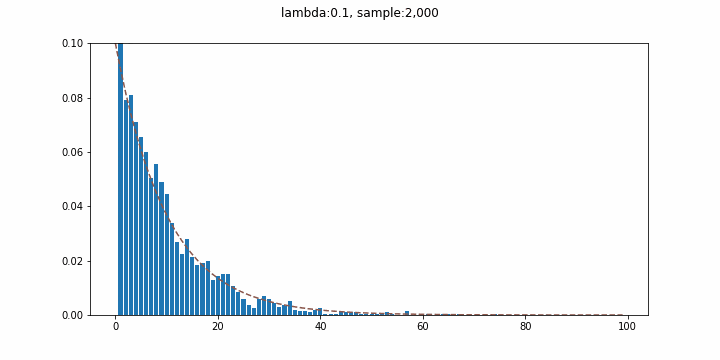
連続的な待ち時間分布として有名な指数分布。ここでは発生確率$\lambda = 0.1$の事象が初めて発生するまでの時間の分布を描き、試行回数を増やしていくことで指数分布を再現してみます(実質幾何分布やんというツッコミはあるかもしれない)。
ガンマ分布
指数分布を一般化したものの一つ。
$\alpha$を正の数として、密度関数は以下。指数分布同様に$x\geq 0$で定義されます。
f(x) = \frac{\lambda ^\alpha}{\Gamma(\alpha)} x^{\alpha - 1}\exp\left(-\lambda x\right)
ただし、$\Gamma(\alpha)$は規格化定数。$\alpha = 1$のときに指数分布に合致します。
指数分布が待ち時間分布として初めて特定の事象が発生するまでの時間を表していたのに対し、ガンマ分布は該当事象が$\alpha$回発生するまでの分布に対応します。$\alpha$を1~3まで変化させて分布を生成すると以下のようになります。指数分布($\alpha = 1$)では単調減少の関数系だったのに対し、$\alpha\geq 2$では山形となっており、$\alpha$とともに少しずつ分布のピーク位置が大きい方へずれていくことが確認できます。
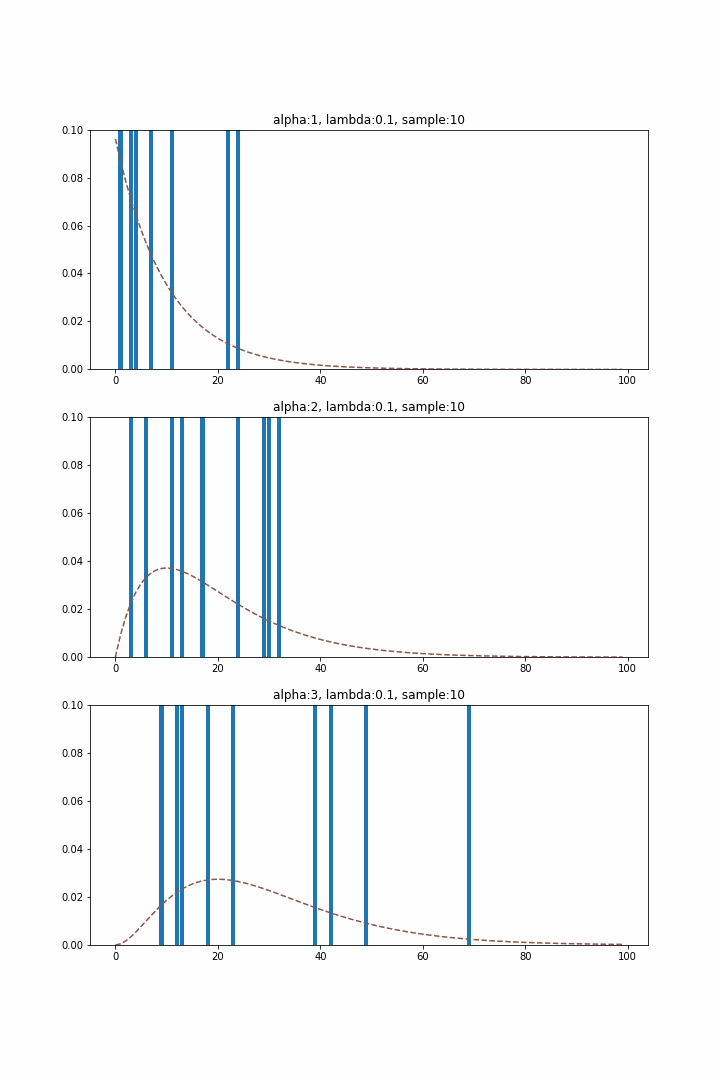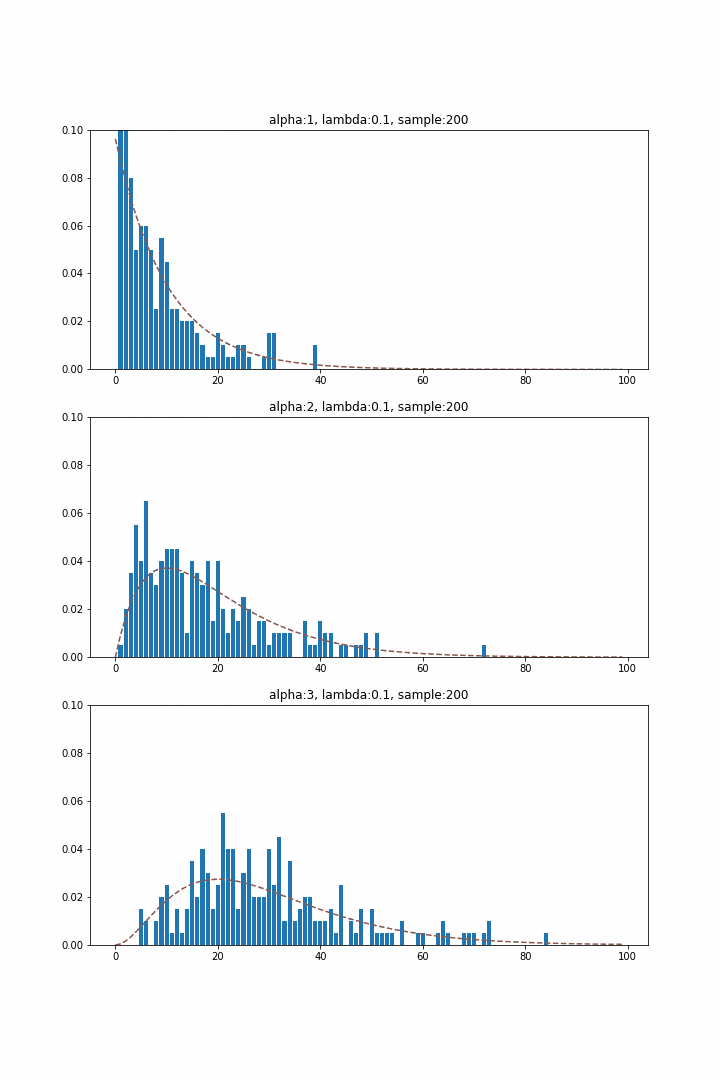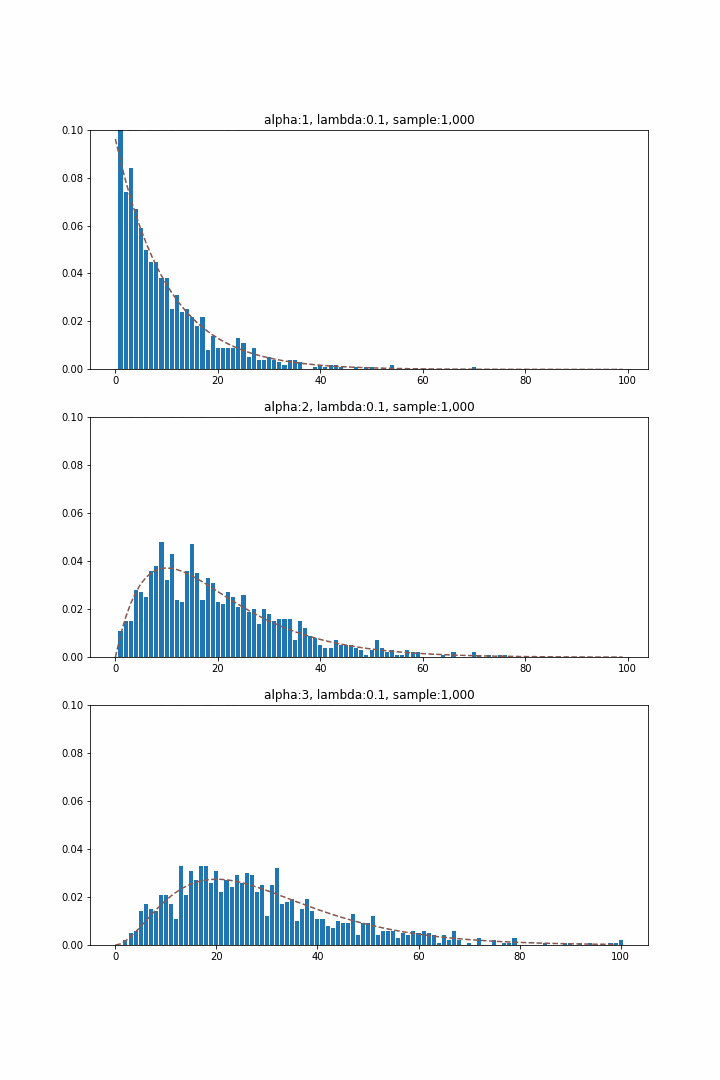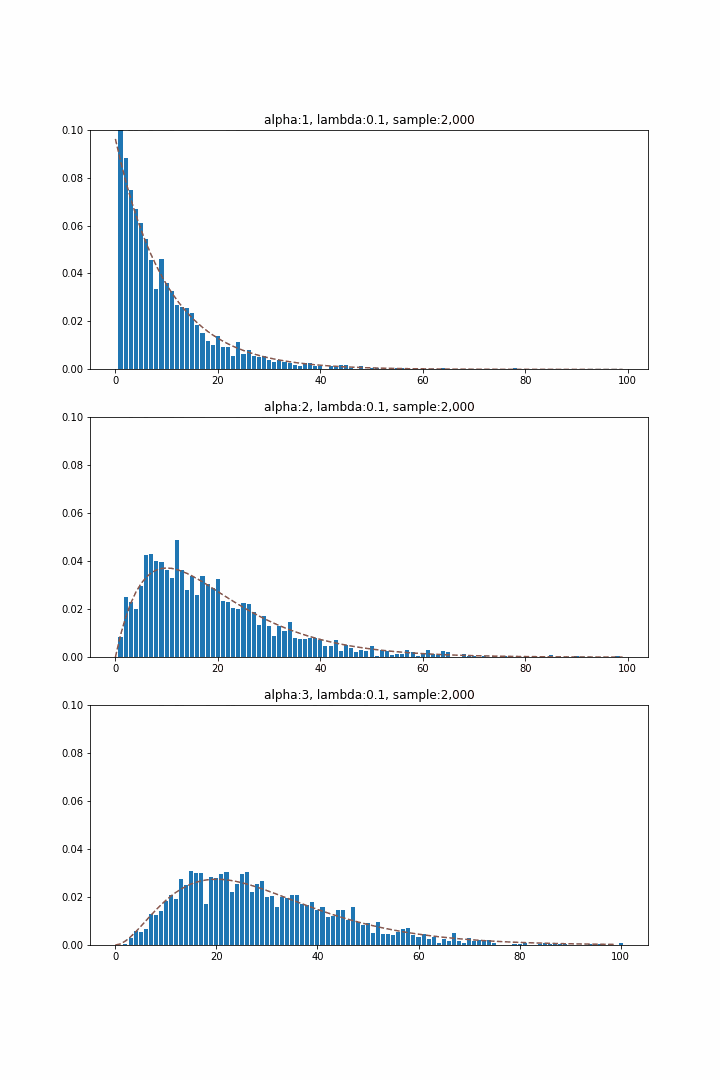
ワイブル分布
指数関数の一般化したものの一つ。
$a,b$を正の数として、密度分布は以下。指数分布、ガンマ分布と同様に$x\geq 0$で定義されます。
f(x)=\frac{bx^{b-1}}{a^b}\exp\left(-\left(\frac{x}{a}\right)^b\right)
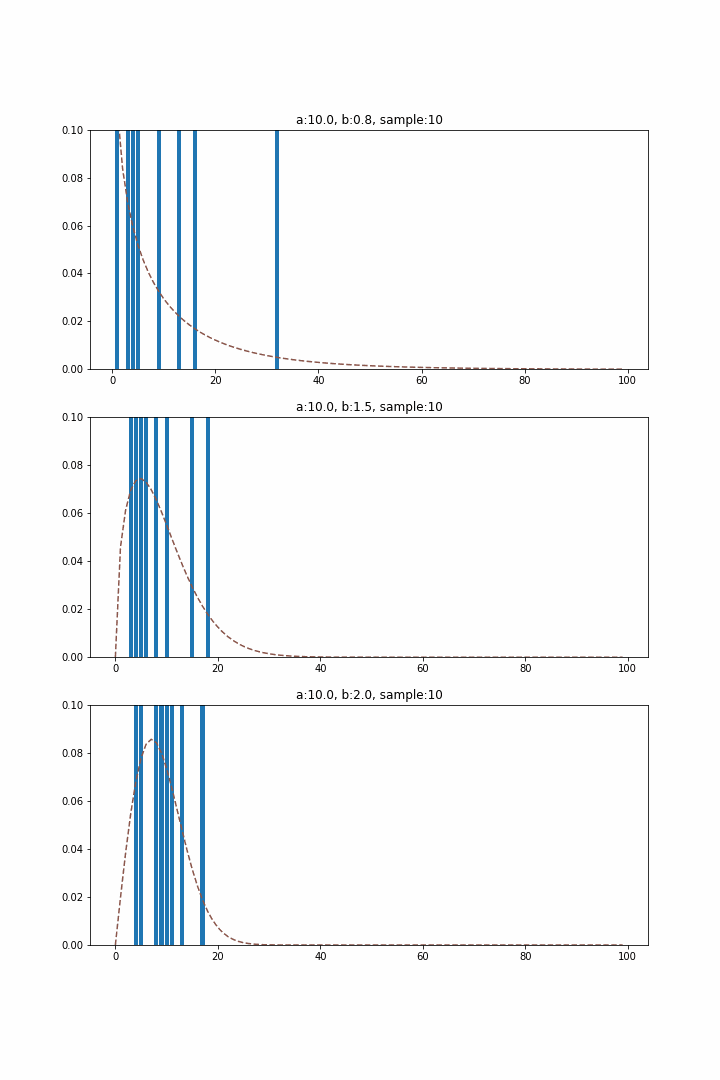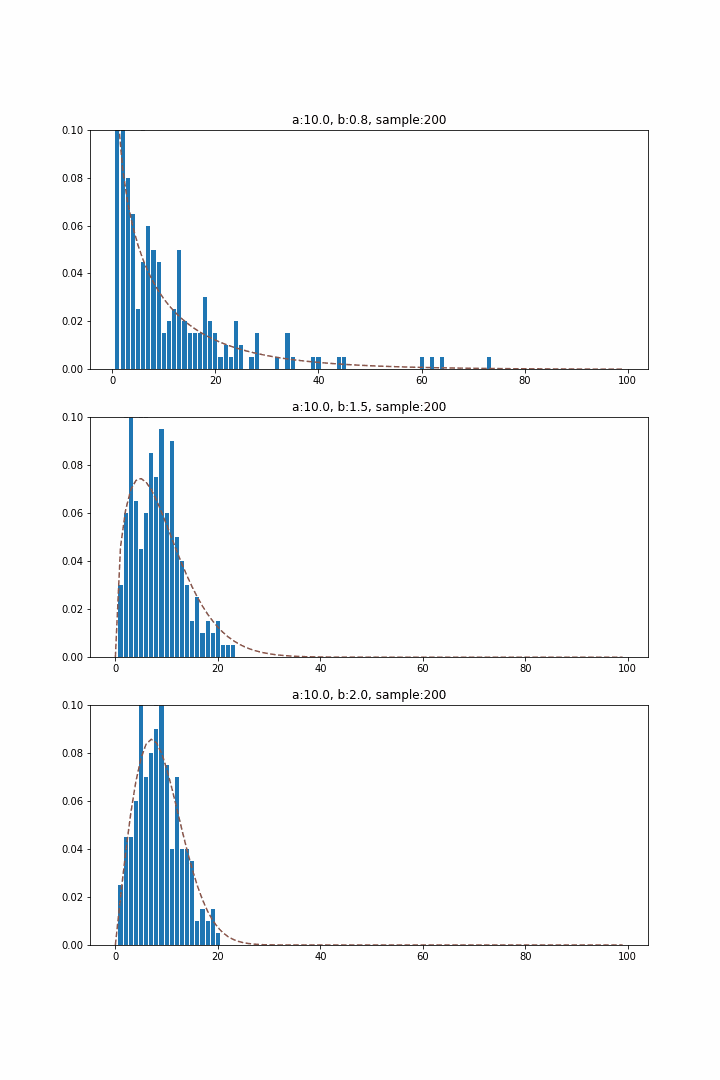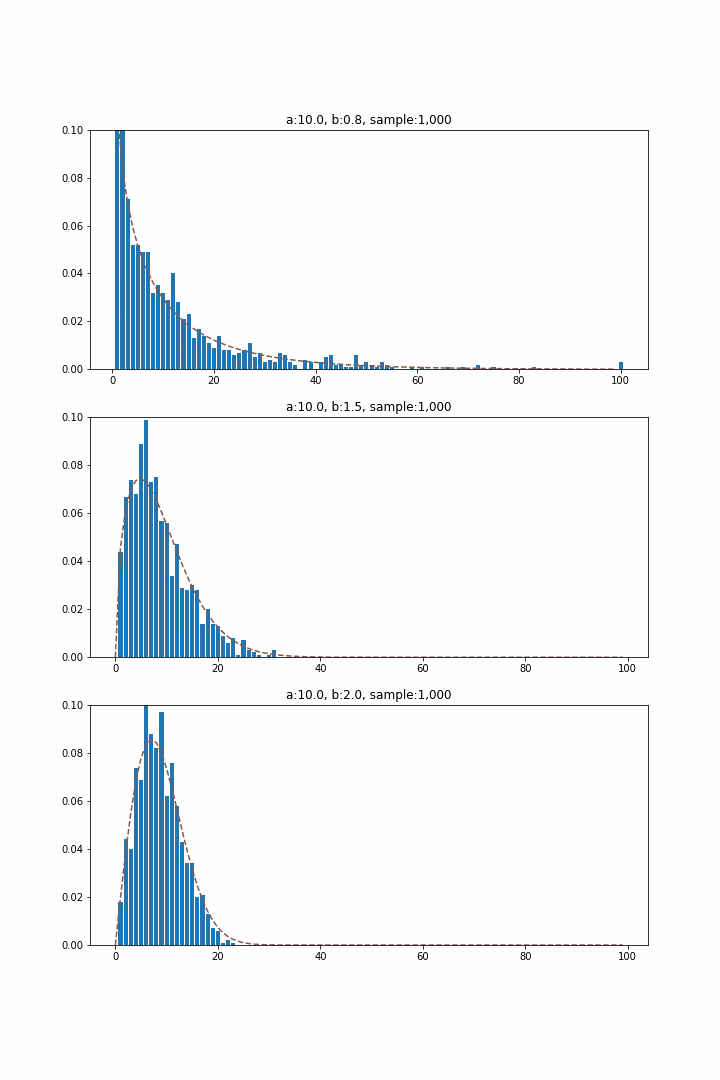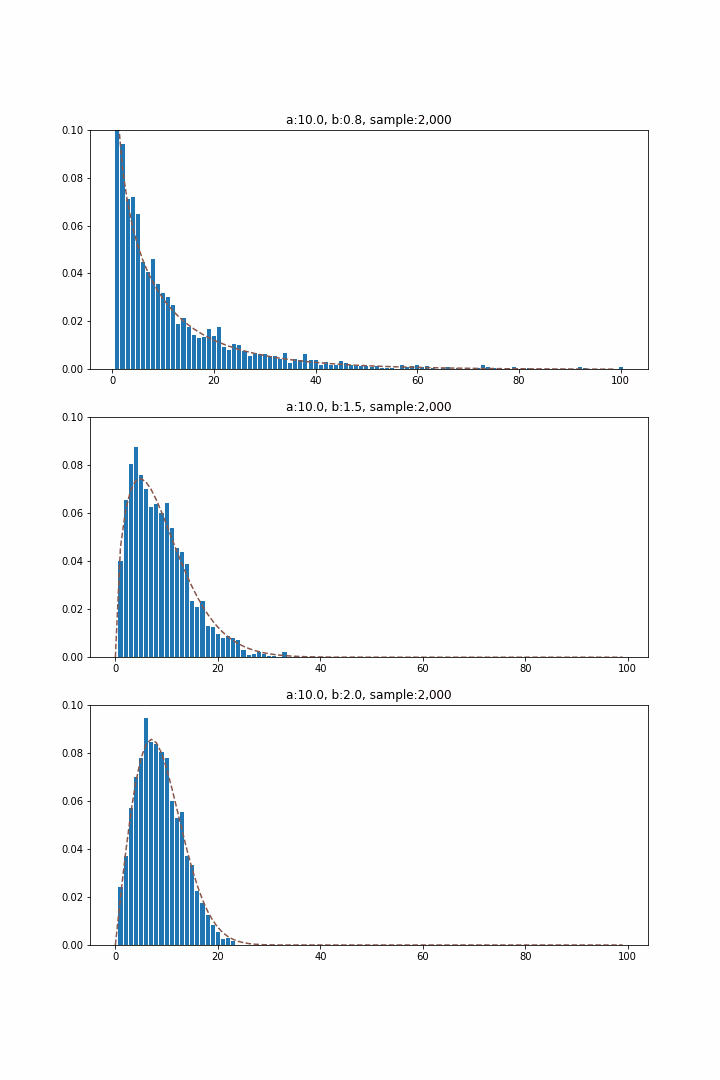
ガンマ分布は待ち時間分布としての指数分布を発生回数起点で一般化したものであるのに対し、ワイブル分布は発生確率に時間依存性を許容した一般化に対応するため、故障現象を説明するためによく用いられます。発生確率は以下の式で表され、$b=1$の場合に時間に対する依存性がなくなり指数分布に合致します。
\lambda(x)=\frac{b}{a^b}x^{b-1}
ここで、$b$は発生確率の時間依存性の指数部分を決める項で、1より大きければ単調増加、小さければ単調減少となり、それぞれ摩耗的な故障、初期的な故障と対応付けることが可能です。
おわりに
いくつかの有名な統計分布について、計算機実験によって再現してみました。
ピュアに数式を変形していくことで理解していくほうが圧倒的にエレガントだとは思うのですが、数式変形で得られた発生メカニズムをもとに、計算機実験で再現すると多面的な理解が得られてこれもまた良しという感じです。
実際、一通りの実験を通じてなんだか腑に落ちた感があるし、何より自分で組んだ分布の関数の形に収束していく様を自らのコーディングベースで確認できると気持ちよさがあるのでよければトライしてみてください!
今回計算機実験で書いたコードはこちら。
明日のfreeeデータに関わる人たち Advent Calendar 2020は、東北出身の むすび丸 Kurotsuさんです!