M-1グランプリ分析2023；今年の盛り上がり

Last updated at 2023-12-25Posted at 2023-12-25

まえがき

今年も24日にM-1がありました。キャッチフレーズは「爆笑が，爆発する」です。
今年は決勝進出常連組が半分，新顔が半分ということもあり，盛り上がりそうだなあと思っておりました。
幸い，年内の予定が全て終わって余裕がある週末であり¹，先にお風呂入って，ピザを頼んで，ビアサーバ用意して，と準備万端でテレビに向かいました²。

それぞれ面白く，令和ロマンの優勝も妥当だなあ，と思いました。個人的な推しはオズワルドだったんですが敗者復活から上がれず³，さや香の一本目は最高なんだけど二本目でちょっと捻り入れすぎて，受け入れられないんじゃないかなーと思ってたら案の定・・・という感じでしたな。いや，いいコンテンツでした。

果たして爆発したのかな

良い大会でしたが，個人的には「爆発」がなかったような印象。笑いが止まらん！みたいな大爆笑がなくて，「いつ爆発するかな」と思ってるうちに終わっちゃうということが多くて。ヤーレンズなんかは特徴的で，ずっと何か喋っててずっとクスクス面白いんだけど，終わる時にスッと止まる，みたいなパタンが多かった気がしますな。

で，点数的にどうなんかな，と思って分析してみました。
自分でも採点してますが⁴，Githubでもデータがあるし，早速更新されているので興味がある人はお手元で再現してみてください。

データは2016年以降のものを使います。2015に第二シーズンが始まって，その年は審査員がかつてのM1勝者ということだったのでちょっと毛色が違うかな，と。2016年以降のジャッジボードは，入れ替わりもありましたが基本的に安定しているので。

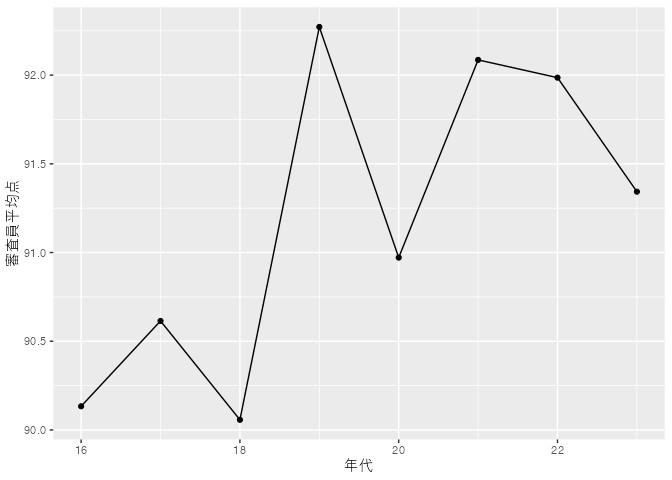
さて，年代ごとの平均点の推移をプロットします。

dat <- read_csv("M1score2023.csv", na = ".")

## Rows: 179 Columns: 36
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## chr  (1): 演者
## dbl (35): 年代, ネタ順, 山田邦子, 博多大吉, 富澤たけし, 塙宣之, 海原ともこ, 中川礼二, 松本人志, 小杉考司, 立川志らく, 春...
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

M1data <- dat %>%
  dplyr::select(-小杉考司) %>%
  pivot_longer(-c(演者, 年代, ネタ順)) %>%
  na.omit() %>%
  mutate(
    PlayerID = as.numeric(as.factor(演者)),
    JudgesID = as.numeric(as.factor(name))
  ) %>%
  filter(年代 > 15)

M1data %>%
  group_by(年代) %>%
  reframe(M = mean(value)) %>%
  print() %>%
  ggplot(aes(x = 年代, y = M)) +
  ylab("審査員平均点") +
  geom_point() +
  geom_line()

## # A tibble: 8 × 2
##    年代     M
##   <dbl> <dbl>
## 1    16  90.1
## 2    17  90.6
## 3    18  90.1
## 4    19  92.3
## 5    20  91.0
## 6    21  92.1
## 7    22  92.0
## 8    23  91.3

やっぱりね。最近インフレ気味だったんだけど，今年はこの3年の流れから行くと低めです。大爆発とはいかなかったな，という印象の傍証にはなりましょう。

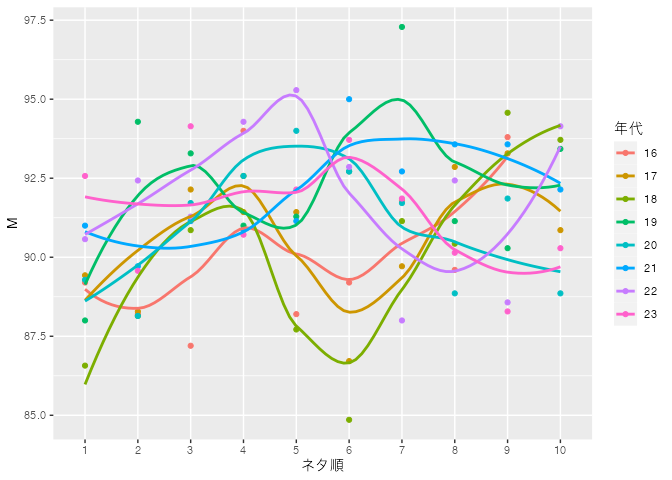
ネタ順を横軸にとって，点数の平均を見るともう少しはっきりします。
点数の推移をスムージングする関数(geom_smoothのデフォルト，loess関数です)で繋げてみるとよくわかります。

M1data %>%
  group_by(年代, ネタ順) %>%
  mutate(年代 = as.factor(年代), ネタ順 = as.factor(ネタ順)) %>%
  reframe(M = mean(value)) %>%
  ggplot(aes(x = ネタ順, y = M, group = 年代, color = 年代)) +
  geom_point() +
  # geom_line() +
  geom_smooth(se = FALSE)

## `geom_smooth()` using method = 'loess' and formula = 'y ~ x'

23年は，92点ぐらいから始まって6番目(マユリカ)でちょっと上がりましたけど，その後下降気味。
昨年のように5番目(さや香)で盛り上がって，最後(ウエストランド)にまたぐっと上がるとか，18年のように7番目(ミルクボーイ)ぐらいでピークがあって終盤戦に，というのがエンタメとしてはいい流れなんじゃないかなとおもいます。それに比べると今年は「イマイチ盛り上がりにかけたな」というのが点数からも明らかですなあ。うーん，難しい。
個人的には，今年最後のモグライダー，滑舌がもっと良ければ大爆発もあったんじゃないかと思ったけど。
皆さんはいかがだったでしょうか。

審査員を審査する

さて，今年のM-1の注目ポイントの一つに審査員として海原ともこが選出されたことがありますな。関西人なら彼女の実力というか面白さというか，その辺は疑うものではないんですが，全国的にはTHE MANZIぐらいしか知られていないのかな。いずれにせよ，審査員はどうやっても賛否両論になってしまうので，引き受けるのも覚悟がいるでしょうが(さらにこうして残った記録で分析までされちゃってまぁ)，一夜明けてネットニュースなんかをみると比較的好意的に受け止められていそう⁵。

で，実際のところどうなんでしょうね。ということでデータを見てみましょう。
まずは今年だけにデータを区切り直して，演者間の相関などをみてみます。

M1.mat <- M1data %>%
  filter(年代 == 23) %>%
  dplyr::select(演者, name, value) %>%
  pivot_wider(
    id_cols = name,
    names_from = 演者,
    values_from = value
  )

judge <- M1.mat$name
M1.mat <- M1.mat[, -1]
player <- names(M1.mat)
row.names(M1.mat) <- judge

## Warning: Setting row names on a tibble is deprecated.

M1.mat %>%
  as.matrix() %>%
  t() %>%
  colSums()

##   山田邦子   博多大吉 富澤たけし     塙宣之 海原ともこ   中川礼二   松本人志 
##        915        903        923        913        928        917        895

合計点は928点と，審査員のなかで一番高めに評価してますな。ちなみに松本人志が今年は辛口で，895点止まりです。
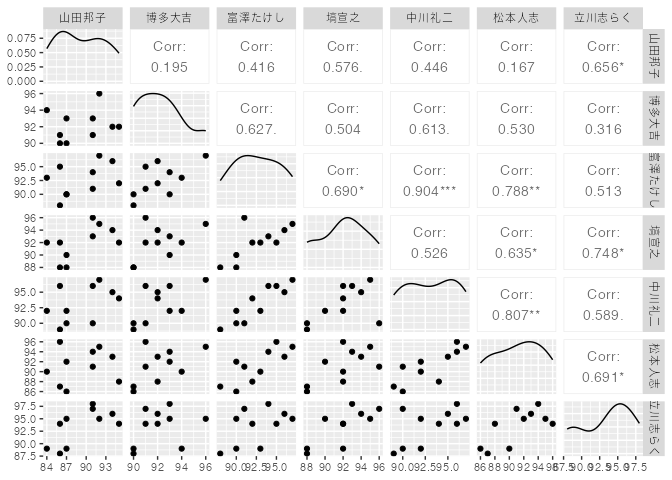
で，相関関係。

M1.mat %>%
  as.matrix() %>%
  t() %>%
  as.data.frame() %>%
  ggpairs()

中川礼二との相関係数が0.846とかなり近い判断。ここは同郷・同期ですからな。面白いの感覚，評価基準が近いんでしょう。で，実は驚いたのがここではなくて山田邦子と松本人志の相関係数。なんと0.007しかないんです。つまりほとんど独立ですわ。関東と関西，女性と男性という違いもあるのかなあ。なんにせよ，こんなに相関関係がないのも，実データを触っている上では珍しい方だと思われます。別にこの2人のどちらかが尖った点数の付け方をしてる！とか言いたいわけじゃないですよ。他の人との相関を見ると0.43–0.56ぐらいの相関はあるし，松本人志も他の人と0.46–0.69の相関があるので。実に興味深い。

確認してみたら，審査員になった去年も松本人志や博多大吉との相関係数が低く，やはり違う視点で評価していることが伺えます⁶。

dat %>%
  dplyr::select(-小杉考司) %>%
  filter(年代 == 22) %>%
  pivot_longer(-c(演者, 年代, ネタ順)) %>%
  na.omit() %>%
  pivot_wider(id_cols = c(年代, 演者), names_from = name, values_from = value) %>%
  dplyr::select(-年代, -演者) %>%
  ggpairs()

繰り返しますが，相関係数が高いことがいい，低いことが悪いというものではなくて。評価次元は多次元である方がいいし，ある人が見つけられない長所を他の人が拾うこともあるので，人選としては素晴らしいと個人的には思ってます。

MDSはいいぞ

別の切り口から可視化してみましょう。
相関ではなくて，実際につけた点数の審査員間距離からMDSをしてプロットします。
MDSがいいのは，点数の順序関係が保持されるようなプロットということ⁷。だいたい，人間の評定は機械の数値化とは違うし，M-1の審査員がよく「1組目が基準点」というように，最初の人に90点をつけたら，次の人はそれより上か下か，その次は上か下か中間か，というように順序的な判断がせいぜい，ということが往々にしてあるわけです。私も今年は最初の令和ロマンを85点にしたもんだから，全体的に低めになっていったし。その程度の精度しかない数字に対して，精緻な統計分析をすることにどれほどの意味がうわなにをするくぁwせdrftgyふじこlp

失礼しました。ともかくMDSは値の大小関係だけを保持して可視化してくれますからな。今回のようなデータに向いているわけです。
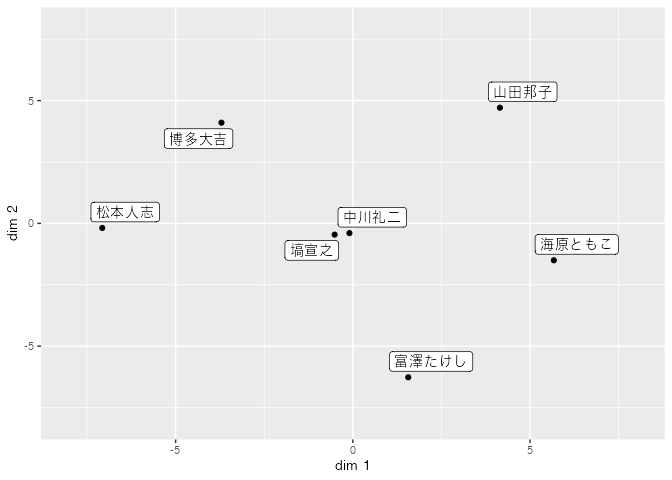
やってみたのがこちら。

M1.dist <- M1.mat %>%
  as.matrix() %>%
  dist()

stress <- c()
for (k in 2:6) {
  tmp <- isoMDS(M1.dist, k = k)
  stress <- c(stress, tmp$stress)
}
# いろんな次元数でストレス値の確認
print(stress, digits = 2)

## [1] 3.3e+00 5.0e-14 6.0e-14 5.2e-14 3.0e-14

# 2次元で十分と判断。
result.MDS <- isoMDS(M1.dist, k = 2)

## initial  value 12.126755 
## iter   5 value 3.518767
## iter  10 value 3.279136
## iter  10 value 3.276741
## iter  10 value 3.276384
## final  value 3.276384 
## converged

result.MDS$points %>%
  as.data.frame() %>%
  mutate(judge = judge) %>%
  print() %>%
  ggplot(aes(x = V1, y = V2, label = judge)) +
  geom_point() +
  geom_label_repel() +
  xlab("dim 1") +
  ylab("dim 2") +
  xlim(-8, 8) +
  ylim(-8, 8)

##                     V1         V2      judge
## 山田邦子    4.14992865  4.7116627   山田邦子
## 博多大吉   -3.70664604  4.1017320   博多大吉
## 富澤たけし  1.56380866 -6.2694379 富澤たけし
## 塙宣之     -0.51303875 -0.4579023     塙宣之
## 海原ともこ  5.67173390 -1.5047157 海原ともこ
## 中川礼二   -0.09553298 -0.3963926   中川礼二
## 松本人志   -7.07025344 -0.1849462   松本人志

2次元で十分なプロットができてそう。松本人志と海原ともこ，博多大吉と富澤たけし，という二つの大きな評価次元があるようです。中川礼二と塙宣之は，点数で見ると中庸なんですな。関西・関東の代表的漫才師，バランスよくみているということでしょうか。素敵な布陣だとおもいます。

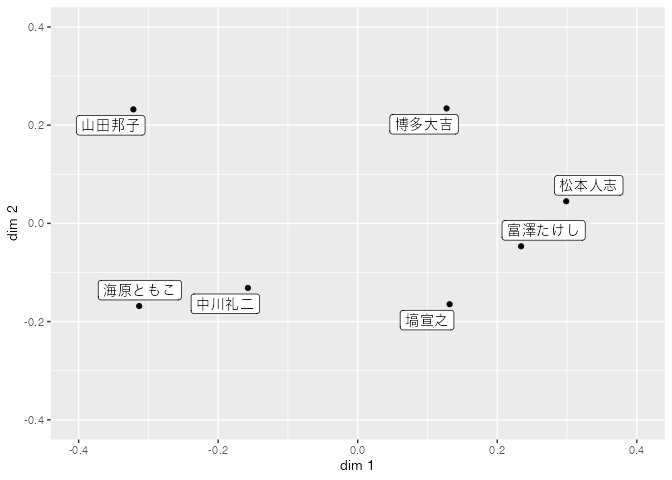
ちなみに相関係数を距離と見立てて(相関が高い＝距離が近い)MDSをすることも可能。評価が相対的で，個人の平均点も違うのですから，標準化したスコア(=相関係数)で分類する方がフェアなのかもしれません。それでプロットしてみたのがこちら。

M1.cor <- M1.mat %>%
  t() %>%
  cor()
M1.cor <- 1 - M1.cor


result.MDS <- isoMDS(M1.cor, k = 2)

## initial  value 17.908761 
## iter   5 value 8.154180
## iter  10 value 7.061288
## iter  15 value 5.847222
## iter  20 value 4.903923
## iter  25 value 4.224041
## iter  30 value 4.131214
## iter  30 value 4.127123
## iter  30 value 4.127123
## final  value 4.127123 
## converged

result.MDS$points %>%
  as.data.frame() %>%
  mutate(judge = judge) %>%
  print() %>%
  ggplot(aes(x = V1, y = V2, label = judge)) +
  geom_point() +
  geom_label_repel() +
  xlab("dim 1") +
  ylab("dim 2") +
  xlim(-0.4, 0.4) +
  ylim(-0.4, 0.4)

##                    V1          V2      judge
## 山田邦子   -0.3214594  0.23207624   山田邦子
## 博多大吉    0.1273405  0.23413507   博多大吉
## 富澤たけし  0.2341641 -0.04663906 富澤たけし
## 塙宣之      0.1317190 -0.16466278     塙宣之
## 海原ともこ -0.3132308 -0.16841644 海原ともこ
## 中川礼二   -0.1573588 -0.13148844   中川礼二
## 松本人志    0.2988254  0.04499542   松本人志

これはこれでまた印象が違って，相関係数でいうと松本・富澤が近くにいる感じに。
ただここでも松本ー山田・海原の軸はあるみたいなので，やはり審査員もジェンダーに配慮したり，多角的に評価できるようにするのは大事だなあ，と思いますな。

標準化するかしないかとか，尺度水準をどう考えるかによって，プロットの形は変わってきます。
どの表現も何らかの意味を持っているように読み取れるし，どれが正解というわけではないけど，色々なものの見方をするというのは，お笑いに限らずデータ分析においても大事なこと。そしてもちろん，しっかり記録して考えるということが大事。
点数をつけるというのは，感覚的なものを言語化し，社会に触れる形にすることでもあります。数字になんてできないよというのではなく，しっかりと数字にして考えるヒントにすることが大事だなあという思いを強くしました。

素敵なお笑いをくれた演者の皆さん，勇気ある審査をしてくれた審査員に感謝。
メリークリスマス＆良いお年を。

追伸　来年もがんばってね，オズワルド！さや香！

実は25日朝にオンライン会議があったのですが，カレンダーを確認せず「今年は終わった」と思い込んでいたので，大遅刻するという大失敗を犯しました。年内最後であって欲しいし，来年以降こんなことないように・・・！ ↩
野田クリスタルがラジオで「日本全国，みんな正座して準備万端見てるだろう」といって，相方に「そんなことないです」と訂正されていましたが，私はちゃんと正座して見るし，子供達には小さい頃から「今日は大事な日だから，演者が演技中はもちろん，全体的に静かにみろ」と申し渡します。 ↩
敗者復活も見ましたが，オズワルドは相変わらず高いレベルで安定したいいネタでした。ただ，そのレベルで完成してしまうと，もう一歩上まで行くのは難しいのかなとも思います。 ↩
こちらのサイトに置いてあります。私の採点も入っているのはご愛嬌。分析に際しては使いませんので。 ↩
たとえばYahoo!で海原ともこ、初Ｍ－１審査員に称賛の声相次ぐ「愛があった」「一生審査員席に」など。 ↩
別の切り口で評価した記事も去年書いてるので，よろしければどうぞ。M-1グランプリ分析；山田邦子さんの評定やいかに ↩
非計量MDSといいます。RではMASSパッケージのisoMDSで実行可能。あるいはsmacofパッケージもおすすめ。 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up