結論;M-1は毎年面白い。
アドカレが近づくたびに,今年はM-1のデータをどうやって調理しようかな,とひぐらし,Rにむかひて,そこはかとなくコードを書き作れば,あやしうこそものぐるほしけれ。
この記事のモデル概略
- 毎年演者も評定者も変わる世界で,どうやって相互比較しようかなあと考えました。
- 松っちゃんは2回を除いてほぼ毎回審査員席に座っているので,彼を基準にしようと考えました。手順は次の通り。
- 毎年の審査員評定から,MDSで審査員のプロットを作ります
- 松っちゃんを座標<1,0>に固定します。そのために,審査員プロットを回転させ,伸縮します。
- 審査員の空間が固定したので,そこに演者をプロットします。
- これでM-1の世界を2次元に押し込むことができた・・・のかな。
この記事のコードにおける去年からの私の成長点
- ソースコード,データはOSFにて公開してあります( DOI 10.17605/OSF.IO/WK4TM)
- tidyr::gatherからpivot_longer, pivot_widerで書くようになったよ。これは便利だホイ。
- nestしてpurrr,を使えるようになったよ。慣れるとすごさがわかるねえ。
はじめに
M-1は言わずと知れた漫才賞レースです。毎年色々なドラマがあります。今年は決勝戦に来たのがほとんど新人!という大波乱必至の回でしたね。
さて毎年面白いんですが,「面白い」の基準は毎年違うのでしょうか。それとも「面白い」はある程度時代,人を超えて共通するものでしょうか。
審査員が審査するわけですから,彼らにはきっと何らかの基準,軸があるはずだ,とは誰しもが思うもの。それを引っ張り出してくるのがデータ解析の面白いところです。
今回もMDSを使ってその辺を探っていきたいと思います。
MDSは一言で言えば(非)類似度行列から地図を作る手法です。これを使うと,評定値から地図が作れちゃうわけで,心の中を探ってやろうってな心理学者にとってはとても嬉しい手法(のはず)。
データは類似度行列ですが,これは普通の評定値から作ることができます。点数の距離がそれに該当するからで,例えば松本人志が90点つけて,上沼恵美子が85点なら,二人の距離は5点,とけいさんできるわけです。
ということで,M-1審査員の評定パターンから,審査員の地図を作ることができます(逆に演者の地図を作ることもできますわよ)。
さてM-1の地図を作ろう,ということですが,困ったことに決勝進出者はもちろん,審査員も毎年少しずつ変わります。
毎年新しい地図を作ることはできるのですが,全部を通じて共通の地図みたいなのが作れない。これでは年度ごとの比較が難しいですね。
三次元方向にMDSを拡張する方法はINDSCALなどあるのですが(Rのsmacofパッケージにあります。昨日の記事も参照),完全なデータがないと作れません。
例えば立川談志が(生きていたら)今年誰に何点をつけたか,というデータは欠損しているわけですから,この方法は使えない。
ところが,かろうじて,毎回のように出ている審査員がいました。そうです,ご存知松本人志。お笑いの神様のように言われていますが(確かにその才能は私,認めるところなんですが),少なくともデータポイントが多いので何かの基準にはなりそうです。
そこで,毎回のMDSの結果(各回は完全データですから)をつかってMDSをした後で,座標合わせをしてやることにしました。MDSの地図は東西南北が特に定まっていませんから,松本人志が常にx軸にあるように回転をかけることは問題ないわけです。また,距離関係は相対的に解釈するしかない=絶対的な距離ではないので,軸の伸び縮みも自由でしょう。なので,毎回松本人志が<1,0>の座標にいるように回転してやれば良いと考えました。こうすることで,他の評定者は松本人志から相対的にどのあたりに離れて存在するか,を考えることができるようになります。
ということで,まず回転をかける関数を作りました。
rotMat <- function(conf, theta, norm) {
# 引数として,回転前の座標,回転角度,基準となる人のノルムを得ます
# RMが回転行列です
RM <- matrix(c(cos(theta), sin(theta), -sin(theta), cos(theta)), ncol = 2)
# 回転させて,ノルムで割ります
rotated <- as.matrix(conf[, -1]) %*% RM / norm
# データフレームにして,審査員の名前を付け足します
rotated <- data.frame(rotated)
rotated$Judge <- conf$rowname
# お返しします
return(data.frame(rotated))
}
全体の座標confを,どの角度で回し(theta),どのように伸縮するのか(norm)を与えてやれば,回転後の座標を返す関数です。
ちなみに面倒なので2次元に限定しています。
あとはこれを使って,毎年のデータをMDSにかけて,得られた座標にこの関数を与えてやれば良いのです。同じことを繰り返すので,purrrの出番!
m1 %>%
# いらない変数を除外します
dplyr::select(-ネタ順, -演者) %>%
# 年代ごとにグループ化,ネストします
group_by(年代) %>%
nest() %>%
# 縦横反転させて・・・
dplyr::mutate(tp = purrr::map(data, ~ t(as.matrix(.)))) %>%
# 欠損値を削除します。これで審査に加わっていない人のデータが削られます
dplyr::mutate(comp = purrr::map(tp, ~ na.omit(.))) %>%
# 審査員同士の距離を計算します。普通のユークリッド距離です。
dplyr::mutate(distance = purrr::map(comp, ~ dist(.))) %>%
# 計量MDSで二次元座標を得ます
dplyr::mutate(Dimension = purrr::map(distance, ~ cmdscale(., k = 2) %>%
data.frame() %>%
tibble::rownames_to_column(.))) %>%
# 座標の中で「松本人志」がx軸となす角度,および松本人志ベクトルのノルムをとります
dplyr::mutate(
# atan2関数を使えば,ベクトルのなす角がわかるよ!
theta = purrr::map(Dimension, ~ atan2(.[.$rowname == "松本人志", ]$X2, .[.$rowname == "松本人志", ]$X1)),
# Rってノルムを計算する関数なかったっけ。面倒だからそのまま計算したけど
norm = purrr::map(Dimension, ~ sqrt(.[.$rowname == "松本人志", ]$X2^2 + .[.$rowname == "松本人志", ]$X1^2))
) %>%
# 先ほど作った回転関数で,他の審査員の座標を回転・伸縮します
dplyr::mutate(rotConf = purrr::map(Dimension, ~ rotMat(conf = ., theta = unlist(theta), norm = unlist(norm)))) -> m1DataSet
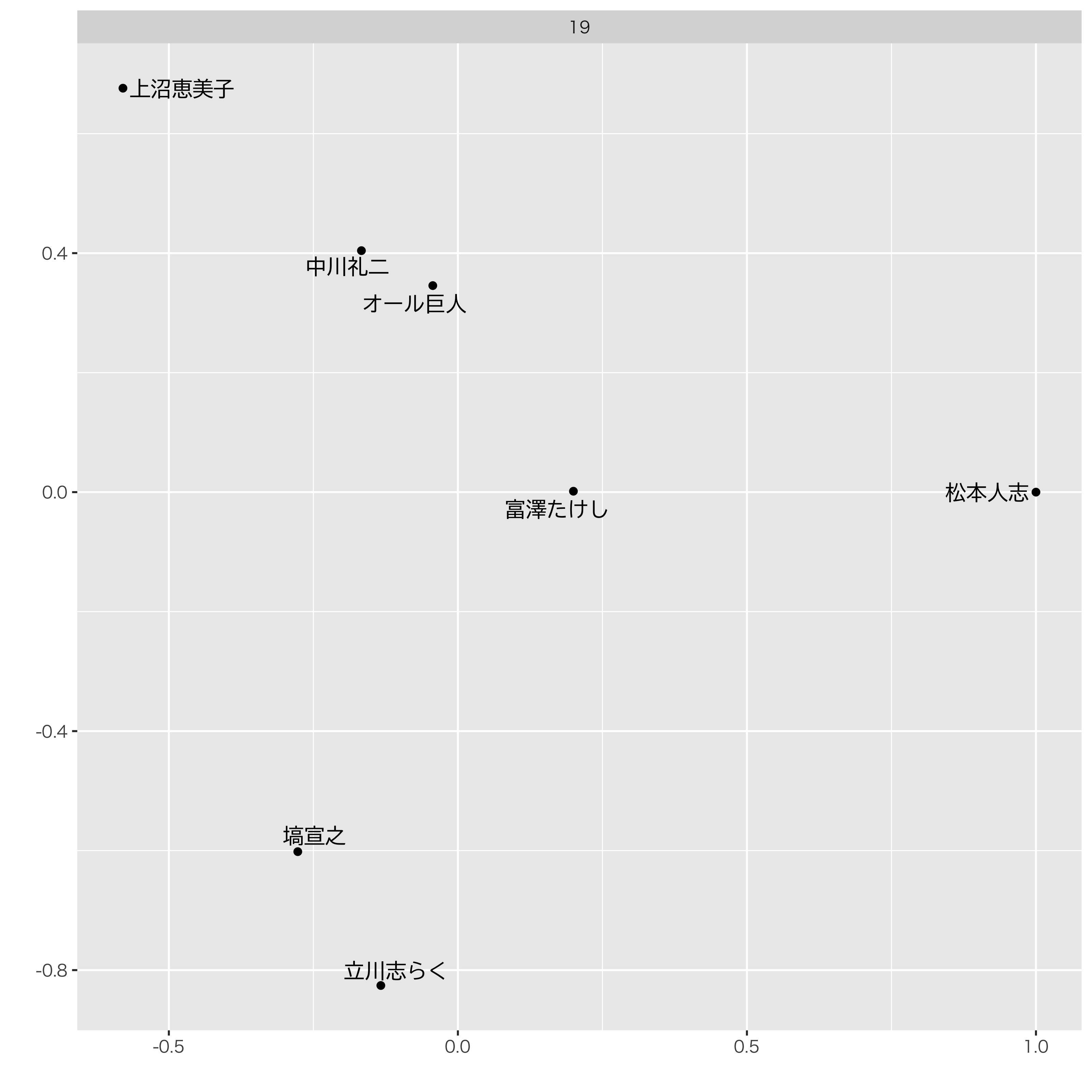
これで得られた審査員空間がこれです。松本人志が常に<1,0>にいますよ。
2010年の渡辺正行は松っちゃんの真逆の軸にいたんだなあ,てなことがわかります。上沼恵美子もちょっと松っちゃんとは違う目の付け所なんだねえ。
今年はどうだったのか
さて,2019年のM-1は過去最高レベルとも言われるほど面白く,激戦,白熱した戦いでした。いい戦いはいい戦いなんですが,こう言う時って,審査員も視聴者に評価されちゃうんですよね。
ひょっとしたらネットでは色々いわれ始めてるのかもしれません。個人的には(いつも言ってますが),審査員は我々常人とは違う経験をしてあの場所にいるわけですから,違って当たり前なんですけど,やっぱり「俺の思った通りにならない!」というのは嬉しくないかも。私も,からし蓮根に対するえみちゃんの評価はちょっと高すぎるんじゃないのー,とか思いましたから。
松っちゃんが<1,0>に固定されていますが,彼は他の人とは違う判断をしてるようです。左上が関西の笑い,右下が関東の笑いの軸でしょうか。
まあでも,極端ではありますが,えみちゃんもある種の笑いの方向性を確立してるんだなあってことがわかります。フムゥ。
では,これと演者の関係はどうなってるんでしょ。
分析
おや,ここまでStanの話が出て来てないぞ?と思った人もいるかもしれません。
そうです,ここまでは確率モデルでも何でもないんですが(もちろんMDSを確率モデルにすることもできるんですが,色々面倒なので今回はパス!),ここからちょっとStanの力を借りたいと思います。
毎年,演者は審査員に評価されるわけですが(そりゃそうだ),審査員の世界のどのあたりに演者がいるのか,これを推定していきたいと思います。
審査員$i$の第$p$次元目の座標を$x_{ip}$とすると,演者の座標もどこかにあるはずで,この演者$j$の座標を$\delta_{jp}$とします。
審査員(の観点)に近ければ近いほど評価が高いと考えると,審査員と演者の距離($d_{ij}=\sqrt{\sum(x_{ip}-\delta_{jp})^2}$)の関数として毎回のスコア$S_{ij}$が得られるはず・・・ですわな。
ということで,こんな回帰モデルにしました。
$$ S_{ij} \sim normal(\beta_{0j}+\beta_{1j}d_{ij},\sigma^2) $$
このもでるから,演者の座標$\delta_{jp}$を探し出すのが今回の目的です。
ちなみにStanコードは次のようになりました。
data{
int<lower=1> N; //審査員
int<lower=1> M; //演者
int<lower=2> D; //次元
vector[D] x[N]; //審査員座標
matrix[N,M] s; //スコア
}
parameters{
vector<lower=-20,upper=20>[D] delta[M]; //探したい座標
real beta0[M]; //回帰係数
real beta1[M];
real<lower=0> sig;
}
transformed parameters{
real<lower=0> d[N,M];
for(i in 1:N){
for(j in 1:M){
real tmp = 0.0;
for(p in 1:D){
tmp = tmp + (x[i,p] - delta[j,p])^2;
}
d[i,j] = sqrt(tmp);
}
}
}
model{
for(i in 1:N){
for(j in 1:M){
s[i,j] ~ normal(beta0[j] + beta1[j]*d[i,j],sig);
}
}
sig ~ student_t(4,0,5);
beta0 ~ normal(0,10);
beta1 ~ normal(0,10);
}
これを毎年のデータに適用していくのですが,その辺は面倒なので「自分でもやってみたい」というひとはこちらのコードを使ってくださいませよ。
結果
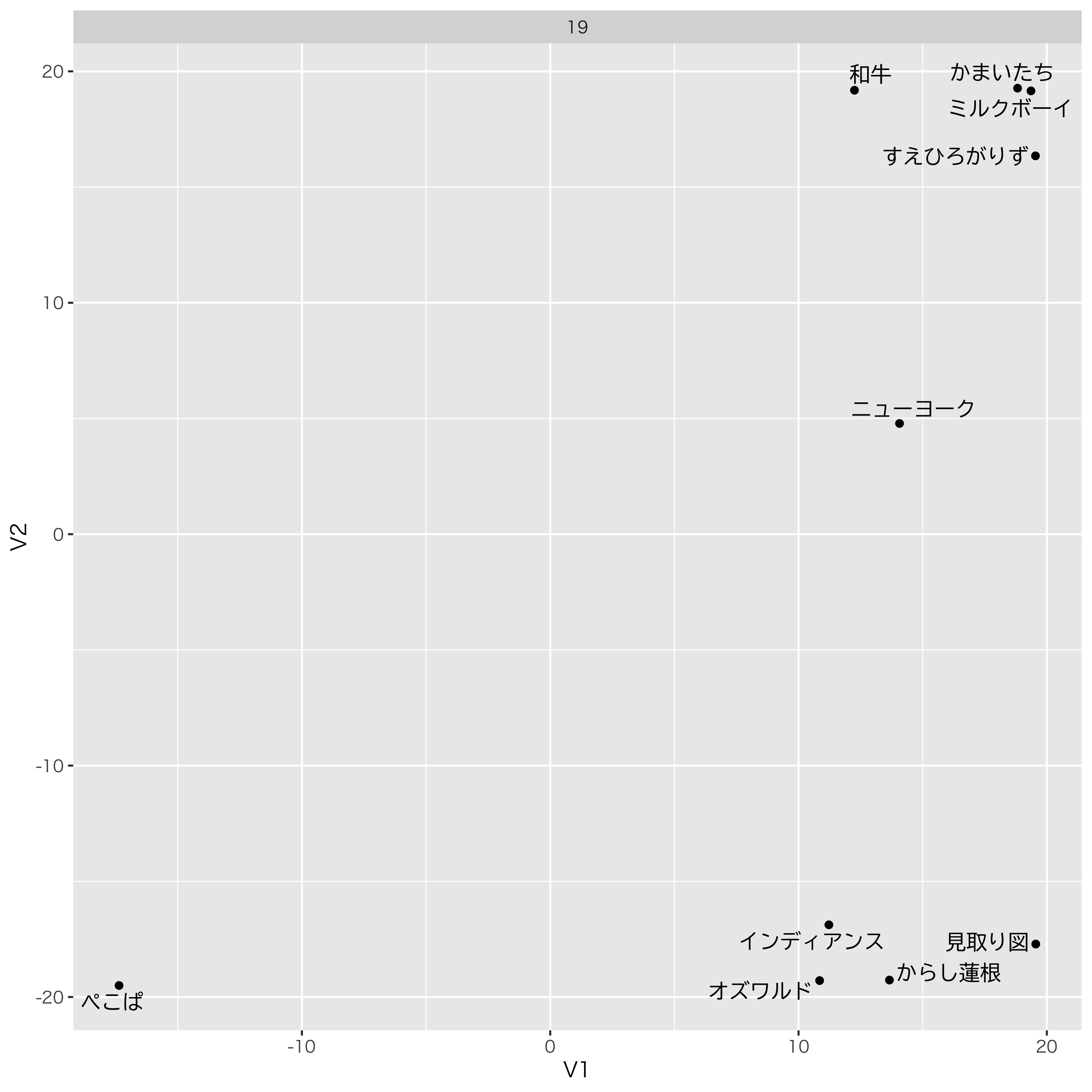
これが2019年の世界です。
かまいたちとミルクボーイは同じ領域,つまり漫才の極が今年はこのへんにあったのでしょうか。同じ領域で戦ったため,審査員も判断しにくかったのかもなあ。和牛も当然そっちの世界にいますね。
いがいとすゑひろがりずも笑いとしては同い時系列だったのか。
ニューヨーク,悪いけどあんまり印象に残ってないです。だから真ん中らへんなんでしょうか。
そしてぺこぱ・・・違う方向で笑いを作っていこうとした,その心意気やよし!来年以降に期待です。
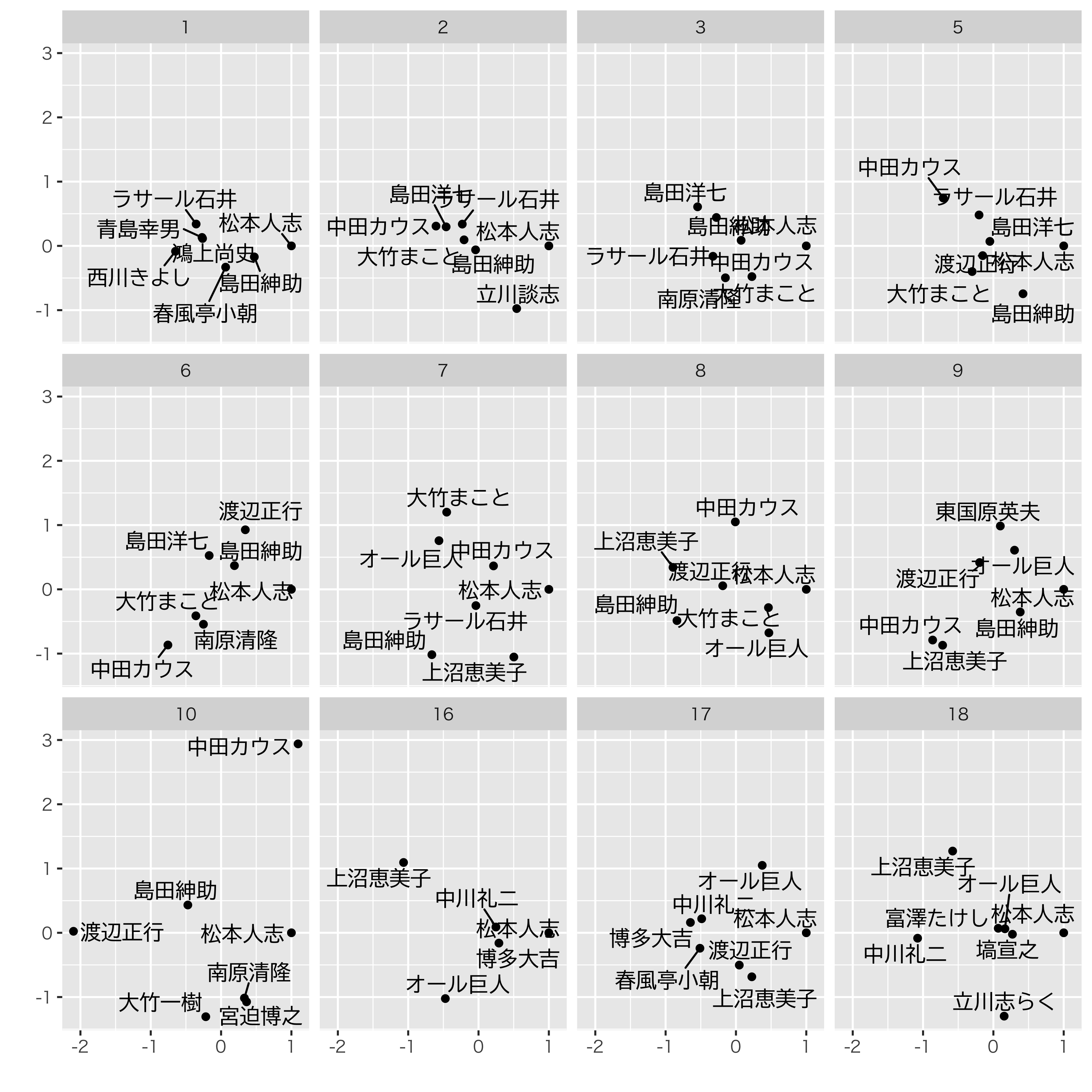
そしてこれが年ごとの演者の世界です。毎年いろんなグルーピングができてますねえ。

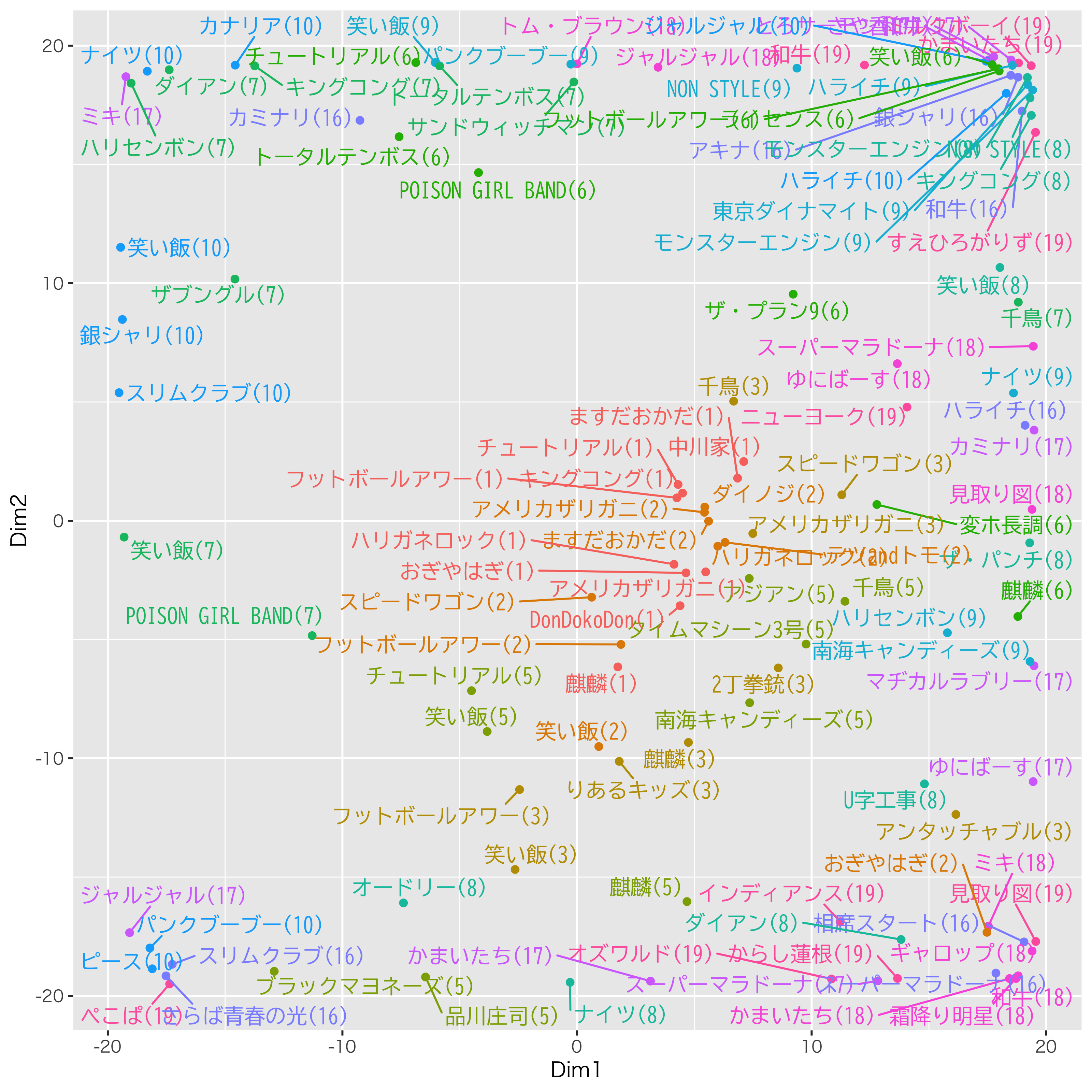
さて,そしてこれが歴代のM-1の演者を一枚の地図にしたものです。(カッコ内が出場年度)
うーん,わかりやすいようなわかりにくいようなw
みなさん,お酒でも飲みながらこの地図を見て,あーでもない,こーでもないと遊んでいただければ。
展望というか補遺というか
今回のこのモデルですが,言うならば「列の座標を先に求めてから,行の座標を求める2段階推定」になっておりまして,この1段目の座標位置合わせがちょっとした工夫点ではあるのですが,実は2段階にしなくても,「行と列の重みを同時に求める方法」ってのはすでにあるんですね。例えばCoombsの展開法モデル(Coombs,1950;足立,2000;清水,2018)なんかがそうですし,あるいは双対尺度法(西里,2010),数量化III類,対応分析なんかもそうです。後者の確率モデルは知らないですけど。
あと,MDSの空間に選好度をプロットする,というのはPrefmapという手法でもあります(岡太・今泉,1994)。今回の手法はPrefmapの確率モデル版みたいなものです。
何れにせよ,データの中の次元,パターンを見つけて,その場所にいろんなオブジェとか色とか追加する,そんな感じでいろいろ楽しめるところが私は好きです。
しかもMDSとかだと別にビッグデータいらないし。身の回りのちょっとした感覚を地図とかモデルで表すってだけでも,楽しいのではないでしょうか。
Stanのおかげで,複雑な確率モデルを数学的に解かなくても,アイディアだけでこうやって楽しめるようになったことは,本当に嬉しいです。科学技術万歳だ。
みなさん,来年もいろんなことを考えて遊んでいきましょうね!
Enjoy Stan! Enjoy Modeling! And Merry Christmas!
今年もStan Advent Calendarを書いてくれた人,見てくれた人にポケットいっぱいの感謝を込めて。
引用文献
- 足立浩平 (2000) 軽量多次元展開法の変量モデル, 行動計量学,27,12-23.
- Coombs,C.H. (1950) PSychological scaling without a unit of measurement. Psychological Review,57,145--158.+
- 西里静彦(2010) 行動科学のためのデータ解析,培風館
- 岡太彬訓・今泉忠(1994)パソコン多次元尺度構成法,共立出版
- 清水裕士 (2018) 阪神ファン-巨人ファンの2大勢力構造は本当か?,豊田秀樹(編)たのしいベイズモデリング,北大路書房,21-32.