はじめに
皆さん、Wolframってる?
というわけでロボカッケー皆さんコンバトラー†[□ □]■━
私は王国騎士ロボットVTuberのKoshiだ🗡💥 (@Koshi_VTuber)
今回は、Wolfram Mathematicaで画像を線画抽出してみただけだ。(発見、備忘録)
環境
Windows 10 Home
Wolfram Mathematica 12
1. 画像を用意する
線画(線ばかりで描いた絵)が望ましい。
今回は私をお借りさせていただいた。(すべり)

2. ソースコードを用意する
お借りしたソースコード
Githubのaomoriringoさんのソースコードを利用させてもらいました。
任意画像の輪郭を数式に変換してプロットする (Mathematica ver.8)
https://gist.github.com/aomoriringo/7706985
3. 実行する
Mathematica 12を起動する
新規ドキュメントを開く
ソースコードを貼り付ける
imageURLに画像パスを入力するだけ
Shift + Enter で実行する
imageURL="";
すごい(小並感)
せっかくなので画像を保存する。

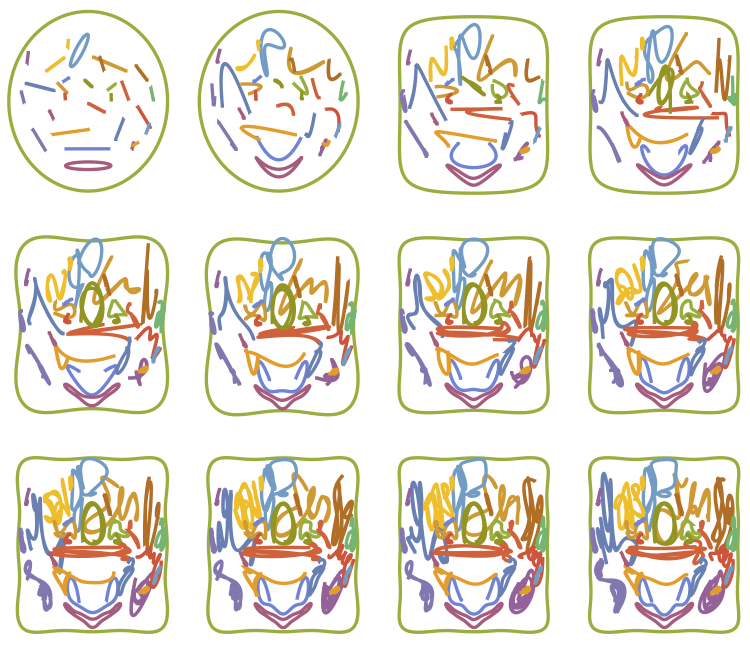
4. 画像の変換過程
画像の変換過程を出力することができる。
続けて、こちらのコードを記述する
Partition[Table[paraplot[n], {n, 1, 12}], 4] // GraphicsGrid
出力結果
5. 数式化
続けて、こちらのコードを記述する
curves = makeFourierSeries[#, t, 200] & /@ fCs;
Style[Map[Short, Rationalize[curves, 0.002]], 16] // TraditionalForm
出力結果(数式化)
{{(5053 cos(t))/53+693/19 cos(2 t)+421/19 cos(3 t)+<<612>>+1/157 sin(200 t)+3864/19,<<1>>},{-((2115 cos(t))/19)+1720/37 cos(2 t)+626/17 cos(3 t)+<<588>>+18466/27,(801 <<1>>)/17+<<575>>},{-((3734 cos(t))/23)+<<586>>+1/181 sin(200 t)+5351/10,<<1>>},{-((482 cos(t))/9)-289/29 cos(2 t)-2131/16 cos(3 t)+<<609>>+9481/16,<<1>>},{(437 cos(t))/10-586/17 cos(2 t)+415/19 cos(3 t)+<<602>>+1/12 sin(199 t)-1/28 sin(200 t)+4357/22,<<1>>},{-((707 cos(t))/19)+319/20 cos(2 t)+93/43 cos(3 t)+<<571>>+21691/24,(487 <<1>>)/10+<<608>>},{<<566>>+3322/7,-((2521 cos(t))/27)+<<579>>+1/95 sin(200 t)-6353/24},{(651 cos(t))/11-10/23 cos(2 t)-143/14 cos(3 t)+<<592>>+1/44 sin(200 t)+7698/25,<<1>>/25+<<581>>},{-((148 cos(t))/25)-349/20 cos(2 t)+<<588>>+21068/25,<<1>>},{<<578>>+1/172 sin(200 t)+28448/53,(661 cos(t))/31-89/48 cos(2 t)+<<593>>+1/27 sin(200 t)-7891/16},{<<583>>+43192/47,(1457 cos(t))/20-277/11 cos(2 t)-32/9 cos(3 t)+<<595>>},{(2139 cos(t))/14+<<569>>+12314/23,(6 cos(t))/31+4094/53 cos(2 t)+<<576>>},{-((1372 cos(t))/11)+573/5 cos(2 t)-866/33 cos(3 t)+<<606>>+6146/15,<<1>>},{(775 cos(t))/33-3/2 cos(2 t)-231/37 cos(3 t)+<<414>>+9103/17,<<1>>},{-((345 cos(t))/37)+101/7 cos(2 t)+<<576>>+1/35 sin(199 t)+1/73 sin(200 t)+33183/34,<<1>>/3+<<610>>},{(306 cos(t))/11+31/20 cos(2 t)-141/10 cos(3 t)+<<524>>+1/266 sin(200 t)+15803/21,<<1>>},{-((986 cos(t))/31)-861/16 cos(2 t)+<<565>>+6383/18,<<1>>},{-((877 cos(t))/33)-904/27 cos(2 t)+361/17 cos(3 t)+<<562>>+15307/22,-((226 <<1>>)/11)+<<535>>},{<<517>>+1/247 sin(<<1>>)+1/231 sin(200 t)+31703/40,-((7253 cos(t))/117)+<<547>>},{<<390>>+1/340 sin(147 t)+1/494 sin(152 t)+1003/12,-((1079 cos(t))/28)+1267/27 <<1>>+<<467>>},{<<372>>+1/474 sin(194 t)+8831/14,-((3608 cos(t))/79)-229/16 cos(2 t)+<<519>>},{-((113 cos(t))/9)-7 cos(2 t)+<<301>>+1/457 sin(121 t)+4726/5,<<1>>},{-((29 cos(t))/12)+57/10 cos(2 t)+<<231>>+1/382 sin(77 t)-1/367 sin(85 t)+4349/11,<<1>>},{-((107 cos(t))/22)+132/23 cos(2 t)+32/27 cos(3 t)+<<175>>+1/456 sin(88 t)+1/481 sin(89 t)+1747/15,<<1>>},{-((9 cos(t))/19)+17/11 cos(2 t)-173/14 cos(3 t)+<<225>>+1/494 sin(110 t)+15960/23,<<1>>/7+<<375>>},{<<247>>+9017/24,-((499 cos(t))/33)+346/19 cos(2 t)+<<347>>+1/492 sin(147 t)-9329/16},{-((350 cos(t))/17)+22/3 cos(2 t)+132/25 cos(3 t)+<<217>>+1/387 sin(30 t)+1/453 sin(36 t)+3409/9,<<1>>},{<<330>>+1/491 sin(<<1>>)+1/440 sin(115 t)+109983/127,(389 cos(t))/37+<<312>>},{<<177>>+3680/13,-((306 cos(t))/11)+481/35 cos(2 t)+102/19 cos(3 t)+<<242>>}}
最後に、
コードを理解して改変したら、もっと面白くなりそう
以上、Unityゲーム王国騎士ロボットVTuber Koshiがお送りしました!
†■━ †■━ †■━ †■━ †■━ †■━ †■━
もし、この記事が役に立ったら、
「いいね」「ストック」
押してね🗡💗
私のステータスだ⚔共にこの世界を救おう
Twitter⚔ twitter.com/Koshi_Vtuber
YouTube⚔ t.co/I9eMMgpS8P?amp=1
niconico⚔ nicovideo.jp/user/90553212
bilibili⚔ space.bilibili.com/476988586
公式HP⚔ koshi-4092b.firebaseapp.com
参考
Mathematicaで任意画像の輪郭を数式に変換する
https://aomoriringo.hateblo.jp/entry/2013/11/30/074758