論文を読んでたら**PSNR(Peak signal-to-noise ratio:ピーク信号対雑音比)**を訓練の評価に使っていたのがあったので、実装してみました。画像の拡大、縮小といった超解像ではよく出てくる概念です。
ざっくり言ってPSNRって?
(拡大や縮小、圧縮などで)画像がどれだけ劣化をしたかを示す値。値が小さいほど劣化していて、大きいほど元の画像に近い。
Wikipediaによると以下の式で定義されます。
$$PSNR=10\cdot\log_{10}\frac{MAX_I^2}{MSE} $$
本来の定義はこの式です。MSEは2つの画像の画素ごとの平均2乗誤差、$MAX_I$は画素値の取りうる最大の値で、0~255なら255、0~1.0なら1です。機械学習では大抵0~1のスケールに変換するため、後者の$MAX_I=1$が多いと思います。
なぜこれが劣化の尺度になるのかというと、MSEは画像がどれだけ違うかという距離を表します。MSEが大きいほど2つの画像が異なるというわけです。上の式から、もしMSEが大きければPSNRは小さくなるので、PSNRの値が小さいほど画像が劣化(異なっている)ということができます。
ちなみに、上の式では画像が同一の場合はPSNRは定義できません(MSE=0で割ることになるので)。ただし、桁落ちのことを考えるとディープラーニングのような数値計算では次のようにしたほうがいいと思います。
$$PSNR=10\cdot\log_{10}\frac{MAX_I^2}{MSE+\epsilon} $$
εは$10^{-7}$とか微小な値です。これで同一画像でもNaNではなく、PSNRは十分大きな値となります(εが大きすぎて潰れてしまった場合は調整してください)。今回はこの式を使います。また$MAX_I=1$という前提を置くと、
$$PSNR=-10\cdot\log_{10}(MSE+\epsilon)=-10\cdot\frac{\ln(MSE+\epsilon)}{\ln10} $$
となります。Kerasの場合は10を底とした対数の関数がないので、底の変換公式により自然対数lnに変換します(高校数学って大事ですね!)。
Kerasのジェネレーターもどき
通常はImageDataGeneratorなどで画像を読み込ませるのですが、説明のために「縮小→拡大」のできるジェネレーターを作りました。今やりたいことは、オリジナルの画像と、縮小→拡大した画像との間でどれだけ画質が劣化しているかをPSNRを用いて計算するということです。これをリサイズのアルゴリズムを変えて見ていきます。
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
from keras.objectives import mean_squared_error
import keras.backend as K
# ここに画像一覧を入れる。今はレナ1枚だけあるものとする
images_list = ["lenna.png"]
# データジェネレーターを模したもの
def data_gen(resize_method=Image.NEAREST, batch_size=1, return_original=False):
images = []
while True:
for imgfile in images_list:
with Image.open(imgfile, "r") as img:
# return_orginal = Trueの場合はオリジナルを返す
if return_original:
images.append(np.asarray(img))
# それ以外は1/2に縮小→倍に拡大をする
else:
x = img.resize((img.width//2, img.height//2), resize_method)
x = x.resize((img.width, img.height), resize_method)
images.append(np.asarray(x))
if len(images) == batch_size:
# 255で割って返す
batch = np.asarray(images) / 255.0
images = []
yield batch
Pillowで画像を読み込んでnp.asarrayでNumpy配列に変換するというよくある例です。説明のためのコードなので詳しくは気にする必要ないです。ちゃんと読み込めるか確認しましょう。
if __name__ == "__main__":
# オリジナル
original = next(data_gen(return_original=True))
# 縮小→拡大
resize = next(data_gen(resize_method=Image.NEAREST))
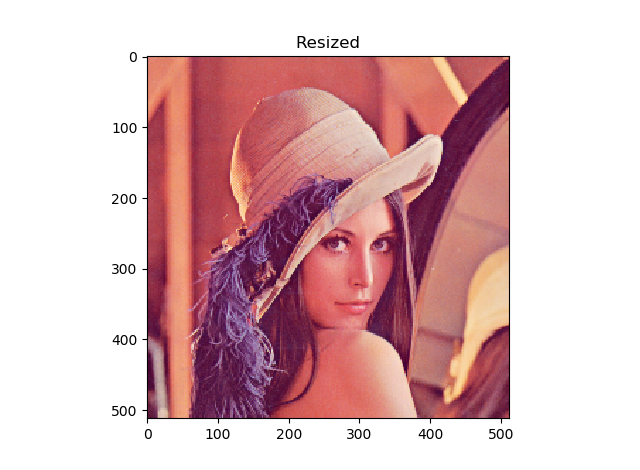
plt.imshow(original[0])
plt.title("Original")
plt.show()
plt.title("Resized")
plt.imshow(resize[0])
plt.show()
リサイズ方式がNearest Neighbour(k-NNとは違う。もっとも基本的な画像補間アルゴリズム)なので、リサイズしたほうがゴツゴツした感じになっているのがわかります。
PSNRのKeras実装
さて先程の式を実装します。Kerasの評価関数で用いることを前提としているので、テンソル演算となっているのをご了承ください。
# PSNRの計算
def psnr(y_true, y_pred):
n_samples = K.int_shape(y_true)[0]
# element-wiseなMSEを取るために平滑化する
mse = mean_squared_error(K.reshape(y_true, (n_samples, -1)), K.reshape(y_pred, (n_samples, -1)))
# 10の対数がないので底の変換公式より(0 divideを避けるためにεを足す)
return -10.0 * K.log(mse+K.epsilon()) / np.log(10)
y_true, y_predとも(バッチサイズ, y, x, チャンネル)という形のテンソルであることを前提とします。ここではy_trueにオリジナル画像、y_predに縮小→拡大した画像が入ります。1行目はバッチサイズを取っています。
2行目はMSE(平均2乗誤差)の計算。keras.objectives.mean_squared_errorを使うと簡単にできるのですが、ピクセル間でMSEを取りたいので、2階のテンソルに変換しています。
3行目は先程の式にならってPSNRを計算します。環境ごとのεはK.epsilon()で計算できます。
画像補間アルゴリズムの比較
ではこの関数を使って画像補間アルゴリズムを比較してみましょう。Pillow.Imageにも定義されていますが、一般的に補間アルゴリズムは最近傍法(Nearest Neighbour)、バイリニア法(Bilinear)、Lanczos法などいろいろあります。
よく「最近傍法は粗い、Lanczos法はきれい」と言われますが、それをPSNRを使って計測してみましょう。これまでと同様に、オリジナルの画像と、半分のサイズに縮小→元のサイズに拡大した画像とを比較します。
def calc_psnr(resize_method):
# 画像の読み込み
original = next(data_gen(return_original=True))
resize = next(data_gen(resize_method=resize_method))
# テンソル化
image_true = K.variable(original)
image_resize = K.variable(resize)
# PSNR
psnr_array = K.get_value(psnr(image_true, image_resize))
return psnr_array[0], resize[0]
if __name__ == "__main__":
methods = [Image.NEAREST, Image.BILINEAR, Image.BICUBIC, Image.LANCZOS]
methodds_str = ["Nearest", "Bilinear", "Bicubic", "Lanczos"]
fig = plt.figure(figsize=(8,8))
fig.subplots_adjust(hspace=0.4, wspace=0.1)
for i, (m, ms) in enumerate(zip(methods, methodds_str)):
ax = fig.add_subplot(2, 2, i+1)
db, image = calc_psnr(m)
ax.imshow(image)
ax.set_title(f"{ms} {db:.2f}dB")
ax.axis("off")
plt.show()
関数をテンソル演算で定義したので計算がちょっと面倒なことになっていますが、Kerasで使う際はここらへんを全部やってくれるのであまり気にする必要はないと思います。結果は以下の通り。
確かによく言われているように、Lanczos法がPSNRが一番高くもっとも劣化が少ないということが確認できました。しかしこう数字で確認してみると、最近傍法はあからさまに悪いですね。Bilinear法のように単純な関数でもいいので補間処理入れるとずいぶんマシになるというのがよくわかります。
まとめ
Kerasのバックエンド関数を使いこなすことで、Kerasを使ってPSNRを計算することができました。もちろん評価関数として使えます。
Kerasはもともとディープラーニングのフレームワークですが、GPUがお手軽に使えるので、従来の画像処理をGPUパワーを使って高速に実装できるかもしれません。