ざっくりいうと
学習率$B$とバッチサイズ$\epsilon$、モメンタムの係数$m$の間には関係があり、以下の2つの法則が成り立つ。
- バッチサイズ$B$と学習率$\epsilon$は比例する($B\propto\epsilon$)
- バッチサイズ$B$とモメンタム係数$m$を1から引いた値は反比例する$B\propto \frac{1}{1-m}$
この式を元に異なるバッチサイズに対して効果的な学習率を決めたり、学習率を落とすのではなくバッチサイズを増やして学習の高速化ができるよというのが論文の主張。
元ネタ
Samuel L. Smith, Pieter-Jan Kindermans, Chris Ying, Quoc V. Le. Don't Decay the Learning Rate, Increase the Batch Size. 2017. ICLR 2018
https://arxiv.org/abs/1711.00489
Google Brainが2017年(ICLR2018)に出した論文。この論文では高速化のための手法として位置づけに重点を置いており、ImageNetをResNet-50で76.1%という精度を保ったまま、30分で訓練することに成功したというものです。ちなみにこの記録は現在破られています。
ただし、ここで出てくるバッチサイズと学習率の関係の議論、バッチサイズを上げることで高速化するという事実、精度と高速化のトレードオフをどう取るかという議論はかなり普遍的に使えるので、仮にImageNetの訓練時間の記録は破られても、ここで出てくる議論はまだ十分使えると思います。今回それを見ていきます。
確率微分方程式としてのSGD
ディープラーニングで用いられるオプティマイザーの確率的勾配降下法(SGD)は確率微分方程式として解釈できます。これはSmith & Le (2017)らの主張によるものです。それによると、
$$\frac{d\omega}{dt}=-\frac{dC}{d\omega}+\eta(t) \tag{1}$$
という確率微分方程式で表されます。ここで、$\omega$はパラメーター、$t$は時間の軸で訓練の進みを表します。$C$はコスト関数(すべての訓練サンプルの合計)で、$\eta(t)$はガウス分布のランダムノイズを表します。この$\eta(t)$の解釈は、ミニバッチ内の勾配を推定結果をモデル化したものです。
またSmith & Le (2017)らは、平均$\langle \eta(t)\rangle=0$(自分の注釈:$\langle\cdot\rangle$は多分期待値のオペレーター)、分散$\langle\eta(t)\eta(t')\rangle=gF(\omega)\delta(t-t')$であることを示しました。ここで$F(\omega)$は異なるパラメーター間の勾配のゆらぎの共分散を表します。自分の意見ですが、ここらへんの方程式の展開はとても難しいんでへーぐらいで見ておけばいいと思います。自分もこれを解けって言われたら音を上げてしまいますし、確率微分方程式の導出自体が相当難しいですから1。
ただし、ここで出てくる結論がとても重要です。$g$について解くと、
$$g=\epsilon\bigr(\frac{N}{B}-1\bigl) \tag{2}$$
となります。急に綺麗な式になりました。ここで$g$はなにかというと**ノイズスケール(Noise Scale)**です。
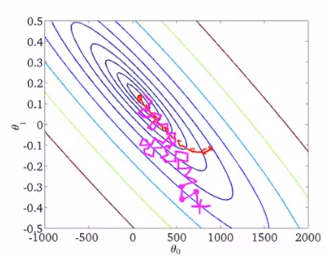
ここからは自分の解説と織り交ぜながらですが、ノイズスケールはちょうどSGDにおける移動する点のゆらぎというのが直感的な解釈になります。ノイズスケール$g$と学習率というのは関係があるのは経験的にわかります。なぜなら、大きすぎる学習率では、このノイズスケールが大きくなってしまうのでより良い解に収束できずに、その周辺をさまよってしまうからです。逆に、ちょうどいい学習率なら、このノイズスケールがちょうどいい幅なので、より良い解に収束できます。逆に学習率が小さすぎれば、ノイズスケールも極端に小さくなります。これは収束に時間がかかりすぎます。つまり、学習率の最適化とはノイズスケールの最適化と同等であるというのがわかるでしょうか。これが式(2)で理論的に示されています。
また、バッチサイズ$B$に対してサンプル数$N$が十分に大きければ(具体的には$N$が$B$のぐらい10倍まで)、冒頭に示した1つ目の式の内容
$$ g\approx \epsilon \frac{N}{B}\tag{3}$$
が出てきます。これは学習率のコントロールと同じことがバッチサイズのコントロールでできるということを示します。これがこの論文の主張のキモです。
例えば、学習率を固定してバッチサイズを5倍にすれば、これはバッチサイズを固定して学習率を1/5にしたことと同じになります。だからバッチサイズを増やすことが学習率を落とすことの代替として使えるのです。
別の言い方をすれば例えば、ある最適なノイズスケールがあったとして、バッチサイズを2倍にして、学習率も2倍にすればノイズスケールは変わりません。これはつまり、バッチサイズを大きくしても同様に学習率も大きくすればだいたい同じ精度でかつ高速化のメリットだけ得られるよということになります。GPUやTPUのデバイスは一般的に大きなバッチサイズのほうが計算のステップが少なくなり、速くなる2ので、精度を落とさなければバッチサイズは大きければ大きいほど良いです。TPUが非常に大きなメモリを確保しているのはこういう背景もあります。
モメンタムのmと学習率の関係
「学習率を落とすこととバッチサイズを増やすことは同じ」というのがわかりましたが、同様のことはモメンタムの係数mを調整することでもできます。ただしこれは若干テスト精度が落ちます。
モメンタムのパラメーターは何だったかというと、指数加重平均を取るのがモメンタムでした。具体的には、$v_t$を移動平均の値、$\theta_t$を観測値としたときに、
$$v_t=m v_{t-1}+(1-m)\theta_t \tag{4}$$
とするのが指数加重平均です。例えば$v_{100}$というのがあり、$m=0.9$とすると、
\begin{align}
v_{100}&= 0.1\theta_{100}+0.9(0.1\theta_{99}+0.9(0.1\theta_{98}+\cdots)) \\
&= 0.1\theta_{100}+0.1\times 0.9\theta_{99} + 0.1\times0.9^2\theta_{98}+\cdots
\end{align}
と指数関数的に減少する加重和を取るから指数加重平均です。モメンタムのオプティマイザーはこれをSGDでやるものですね。これのノイズスケールは次の式になるとのことです。式展開はSmith & Le (2017)にあります。
\begin{align}
g &= \frac{\epsilon}{1-m}\bigr(\frac{N}{B}-1\bigl) \\
&\approx \frac{\epsilon N}{B(1-m)} \tag{5}
\end{align}
という関係が成り立ちます。もし$m=0$ならこれはただの(モメンタムなしの)SGDと同じになりますのでこの式は(3)の拡張であるということがわかります。ちなみにこの議論はモメンタムですが、Adamでも使えます。
この式を見ると、$B\propto\epsilon$と同じように、$B\propto \epsilon/(1-m)$で計算していけば最適な学習率は計算できます。これは確かにそうなのですが、モメンタムの性質上この比例方式は若干テスト精度が落ちます。
なぜなら$\frac{d\hat{C}}{d\omega}$を訓練サンプルあたりの勾配の平均とし、$A$をその「蓄積」とすれば、
\begin{align}
\Delta A &= -(1-m)A+\frac{d\hat{C}}{d\omega}\tag{6} \\
\Delta\omega &= -A\epsilon \tag{7}
\end{align}
という式になります。(6)式は(4)式をモメンタムありのSGDになるようによりフォーマルに書いたものですね。(7)は勾配降下法によるアップデートの定義そのものです。(6)(7)からこの微分方程式を解くと、
$$\frac{B}{N(1-m)} \tag{8}$$
おおよそ**(8)式で表されるエポック数**分の時間軸で、この「蓄積」が進み、指数的にある値に向かうということが示されるということです。具体的な導出はこの論文の末尾に証明が載っているので、必要な方は見てみてください。
直感的には、十分な「蓄積」を終えるために必要なエポック数が増えるから、パラメーターのアップデートの大きさの$\Delta\omega$が抑制されて、収束率が悪くなる。もうちょっとざっくりいうと、(5)式にあわせてバッチサイズを大きくし、同時にmを大きくしてしまうと、より長い訓練エポック数が必要になるから、変更前と同一エポック数だとテスト精度が悪くなりますよ。ということです。
論文での実験
ここまでの理論展開で2つのことがわかりました。ここからはざっくり見ていきます。
- 学習率を落とすことはバッチサイズを上げることと効果は同じ
- 学習率を落とすことはモメンタムの項を増やすのと効果は同じ。ただしテスト精度は若干落ちる
とのことでした。
学習率とバッチサイズの関係の実験
論文ではここから学習率を落としたケースと、バッチサイズ/モメンタム項を増やしたケースで学習曲線が同じよう動きをするのかを検証しています。「16-4」のWideResNetでCIFAR-10を分類したとのことです。
次の3条件を試しました
- 学習率を落とす
- 複合
- バッチサイズを増加させる
こんな感じですね。1はバッチサイズ固定で学習率を1/5ずつ減らす、3は学習率固定でバッチサイズを5倍ずつにする。複合のケースは1回だけバッチサイズを5倍にして、残りは学習率を1/5ずつ減らすというものです。初期のバッチサイズは128です。
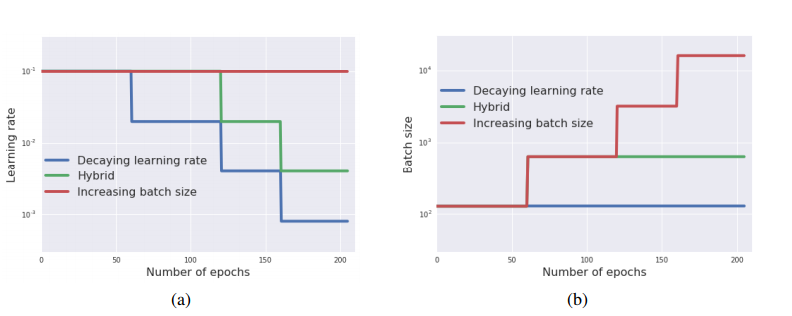
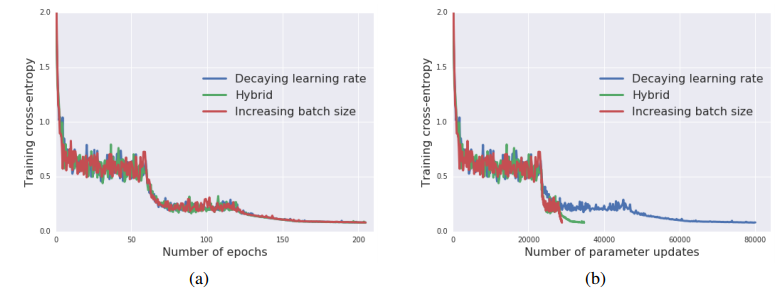
これをただのSGDを使って学習曲線を描くとどのケースも同じになります。
左側のグラフが普通の学習曲線でエポック数を横軸としているのに対して、右側のグラフはパラメーターのアップデート回数(=ミニバッチの適用回数)なので、バッチサイズを増やしたとたんに急にロスが減っているように見えるのがわかります。バッチサイズを増やしたほうが訓練が速く終わるというわけです。
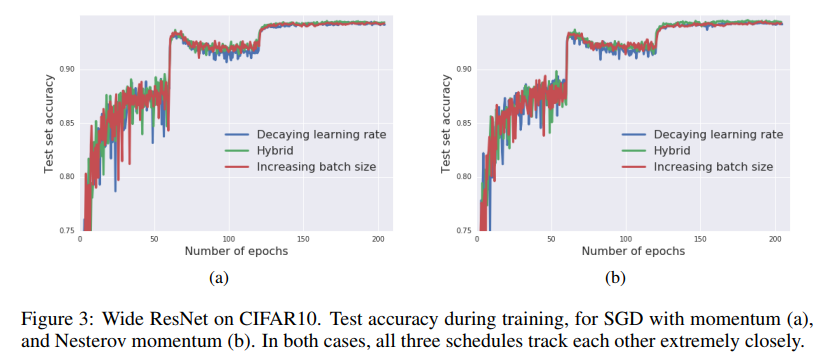
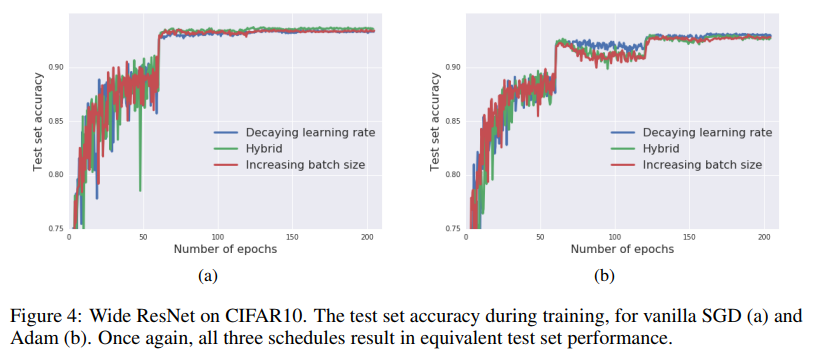
論文ではこのあとモメンタムとAdamのオプティマイザーでも調べていて、これらのオプティマイザーでも学習率とバッチサイズの間に同様の関係を確認することができました。
どれもほとんど同じですね。最終的な精度はAdamよりもモメンタムのほうが若干良さそうなのが気になります。
学習率とモメンタムと関係
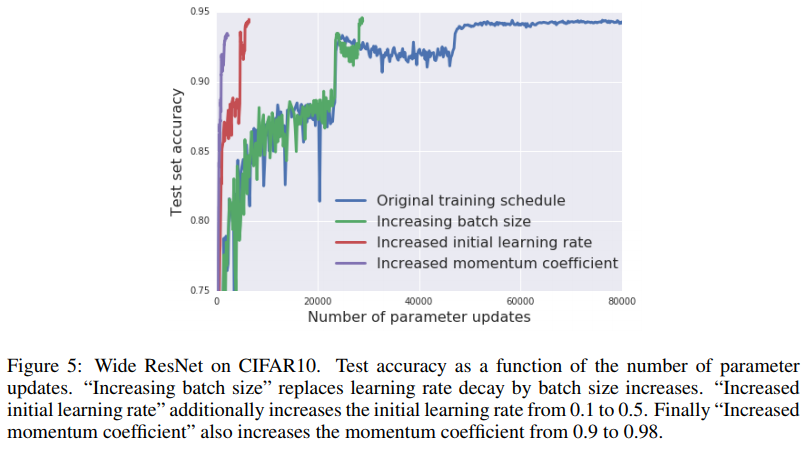
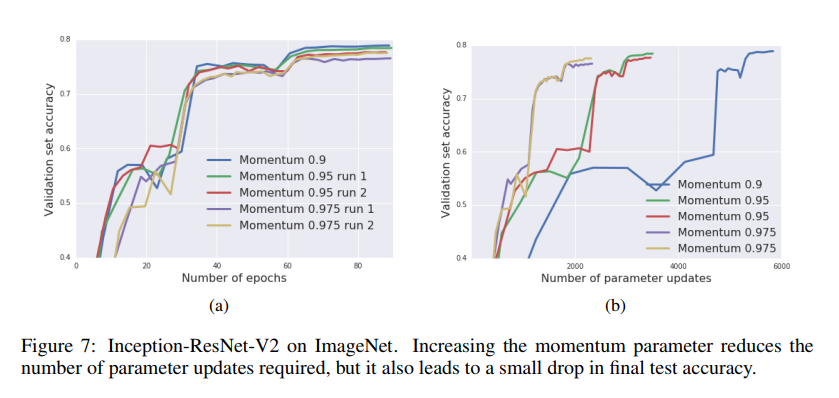
同様にして学習率を減らすかわりにモメンタムの係数を増やしてもほぼ変わらないということが確認できます。
横軸はパラメーターのアップデート回数です。モメンタムの係数を増やすほうがより少ないアップデート回数で訓練が終わることが確認できます。ただし、理論的に確認したとおり、モメンタムの係数を増やすと勾配の「蓄積」が足りなくてテスト精度が若干落ちているのも確認できます。
際限なく初期学習率を大きくできるわけではない
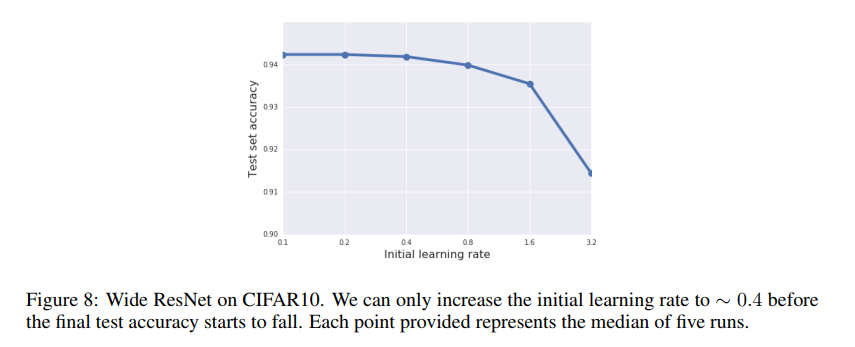
「モメンタムの係数を増やしすぎるとテスト精度が落ちんだから、学習率とバッチサイズの関係に従って$B\propto\epsilon$と延々と最初のバッチサイズと学習率を増やせばよくない?」と思うかもしれません。ただしこれには裏があって、CIFAR-10でどんどん増やしていくとあるところからテスト精度が落ちるようになります。学習率0.1のときのバッチサイズを128とします。
具体的には最初の学習率0.4(=バッチサイズ512)のあたりから若干落ちてきて、3.2(=バッチサイズ4096)はもうだいぶ精度が下がりますね。そううまい話はないよ、ということでしょうか。ただし、この閾値はデータによって変わるので後述のImageNetだとバッチサイズ8192から初めても全然OKだったりします。
ImageNetでの検証
また、この論文はImageNetの訓練についても調べられています。どれも初期のバッチサイズは8192、学習率は3.0、モメンタムの係数を0.9とするのをベースラインとします。Inception-ResNet-V2を使っています。また、ImageNetの画像数は128万枚であるため、「BがNに対して十分小さい」という仮定を満たすために際限なくバッチサイズを上げられないということに注意してください(バッチサイズ60万とかは無理)。
まず1つ目の実験はバッチサイズの変更です。(1)ただ単に30.60,80エポック目で学習率を1/10ずつするという普通の方法、(2)30エポック目でバッチサイズを8192→81920とし、60、80エポック目では学習率を1/10ずつ落とします。
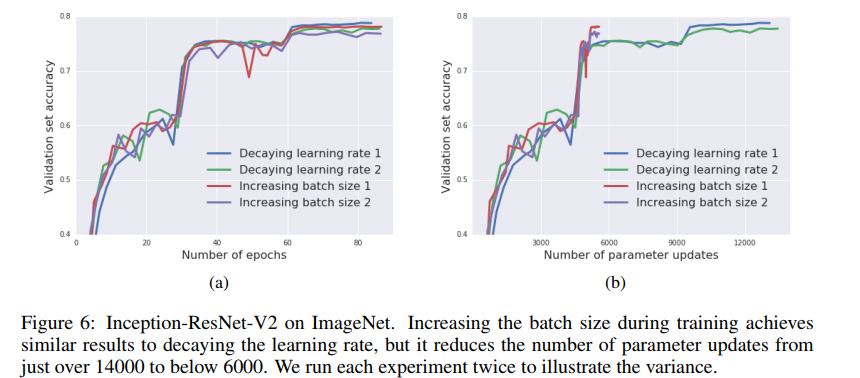
やはりだいたい同じですね。若干(2)のほうが悪くなっているように見えますが、何回もやるとテスト精度は(1)も(2)も似たようなばらつきになったとのことです。
バッチサイズを際限なく増やすのは厳しそうなので、最大バッチサイズを65536という縛りを置くことにします。そこで、初期の学習率とモメンタムの係数を固定し、ノイズスケールの調整はバッチサイズと学習率で調整します。例えば、初期のバッチサイズが32768だったら、バッチサイズはあと2倍できるので、30エポック目でのdecayのみバッチサイズを2倍+学習率を1/5、残りの60、80エポック目ではどちらも学習率を1/10とします。初期条件はバッチサイズとモメンタムの係数で決まり、(1)モメンタム0.9+バッチサイズ8192、(2)モメンタム0.95+バッチサイズ16384、(3)モメンタム0.975+バッチサイズ32768としています。これは式(5)から出てきたものです。
テスト精度は若干落ちているものの、ほとんど気にならない範囲ですね。確かにこれは高速化には有効な方法でしょう。
ImageNetを30分で訓練する
256のテンソルコアからなる半分のTPUポッドを使っています。すべてResNet-50で90エポック訓練させています。
- バッチサイズを8192でずっと訓練する→45分以内にValidation Accuracy76.1%
- 最初の30エポックをバッチサイズ8192で、残りの60エポックをバッチサイズ16384で訓練→30分以内に同精度の76.1%
これにより、高速化に成功しています。多分残りのdecayは学習率で調整したはず。ただし、最初のバッチサイズを16384にすると22分で訓練できたのですが、精度が75.0%とちょっと低かったとのことです。
個人的感想
ImageNetを30分で訓練するというのは「ほえ~頭おかしい(褒め言葉)」って感じですが、ここで出てくる、学習率とバッチサイズの関係、学習率とモメンタムの係数の議論は普遍的に使えてとても有効で面白い話だなと思いました。特にSGDを確率微分方程式の文脈で見るというのが斬新だなと思いました。
続き
自分でも実験してみた
TPUでも大きなバッチサイズに対して精度を出す:
https://blog.shikoan.com/tpu-bigbatch/