TL;DR
- Conv2D, DepthwiseConv2D, SeparableConv2D, Conv2DTrasposeの計算過程をKerasの数値例で確かめた。
- Optunaを使って、これらのレイヤーを組み合わせたモジュール構成の探索を行った。Optunaによると、パラメーター数を減らすことと精度を維持する点では、MobileNetやXceptionの構成は理にかなっていることがわかった。
表記
この記事ではデータ(画像)の軸を次のように表記します。2次元の画像なので、1サンプルあたり(縦, 横, チャンネル)=$(Y, X, C)$の3次元の配列(テンソル)となります。テンソルという言葉が怖ければ、「配列変数」と置き換えて読んでください。
もし、データが1次元(音声や時系列データ)なら1サンプルあたり2次元になりますし、データが3次元(動画)なら1サンプルあたり4次元になります。今回は画像の例、つまり1サンプルあたり3次元で説明しますが、適宜置き換えて読んでください。
実際はミニバッチ学習をさせるので、これにバッチの軸が加わり、画像の例なら(バッチ, 縦, 横, チャンネル)=$(Batch, Y, X, C)$という4次元のテンソルになります。しかし、一般的なニューラルネットワークの場合、バッチ間の計算はやらないことが多いので1、今回は最初の軸は無視して$(Y,X,C)$の3次元で考えます。
Conv2D
最も登場することが多く、また最も一般的な畳込み計算です。まずは入力層も出力層も1層の例を考えます。
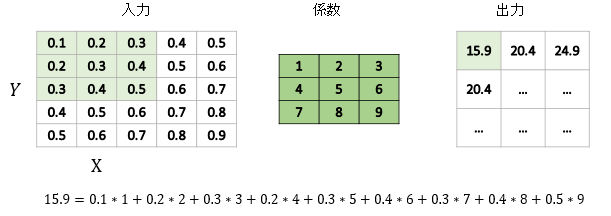
このように、入力の畳み込み係数(カーネル)サイズ分の行列を抽出し、それと係数の行列との要素間の積を取り、足し合わせます。例えば、出力の「15.9」のセルでは、左上の0.1×1+上の真ん中の0.2×2+……という計算をしています。2セル目以降は、入力のデータに対する抽出を1セルずつずらしていきます。これを入力データが末尾まで到達するまで続けます。
入力も出力も多層な例
今までは入力も出力も1層だったのでわかりやすかったですが、入力が$N$層で、出力が$M$層だった場合($N\neq M$)はどうなるでしょうか?次に、$N=2, M=3$のケースを考えます。
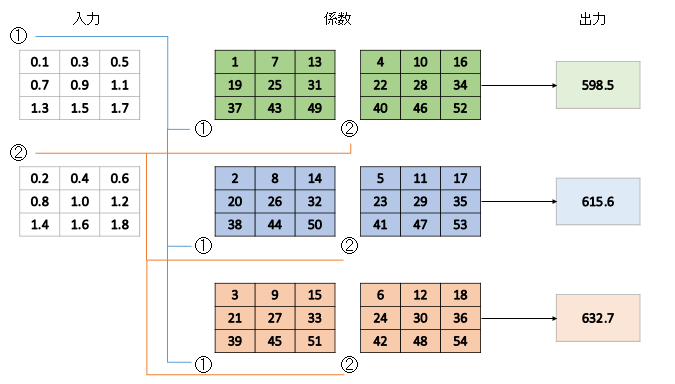
係数のフィルター数は$NM$個になります。出力、入力の層に対応するフィルターを総当たりで導入し、これらの和を取ります。例えば一番上の「598.5」の出力は、
- 0.1×1+0.3×7+……+1.7×49=274.5
- 0.2×4+0.4×10+……+1.8×52=324
- 274.5+324=598.5
という計算を行っています。Kerasで確認しましょう。
from keras.layers import Conv2D, Input
from keras.models import Model
import numpy as np
def normal_conv_two():
input = Input((3,3,2))
layer = Conv2D(3, kernel_size=3, use_bias=False) # 計算を簡単にするためにバイアス項を抜く
x = layer(input)
model = Model(input, x)
weights = layer.get_weights()
print(weights)
print(weights[0].shape)#(3,3,2,3)
weights = np.arange(1, 55).reshape(3,3,2,3).astype(np.float32)
layer.set_weights([weights])
print("weights")
print(weights[:,:,0,0])
print(weights[:,:,0,1])
print(weights[:,:,0,2])
print(weights[:,:,1,0])
print(weights[:,:,1,1])
print(weights[:,:,1,2])
X = np.arange(1, 19).reshape(1,3,3,2) * 0.1
print("input")
print(X[0,:,:,0])
print(X[0,:,:,1])
result = model.predict(X)
print("output")
print(result[0,:,:,0]) # weights[:,:,0,0]*X[0,:,:,0] + weights[:,:,1,0]*X[0,:,:,1]
print(result[0,:,:,1]) # weights[:,:,0,1]*X[0,:,:,0] + weights[:,:,1,1]*X[0,:,:,1]
print(result[0,:,:,2]) # weights[:,:,0,2]*X[0,:,:,0] + weights[:,:,1,2]*X[0,:,:,1]
if __name__ == "__main__":
normal_conv_two()
weights
[[ 1. 7. 13.]
[19. 25. 31.]
[37. 43. 49.]]
[[ 2. 8. 14.]
[20. 26. 32.]
[38. 44. 50.]]
[[ 3. 9. 15.]
[21. 27. 33.]
[39. 45. 51.]]
[[ 4. 10. 16.]
[22. 28. 34.]
[40. 46. 52.]]
[[ 5. 11. 17.]
[23. 29. 35.]
[41. 47. 53.]]
[[ 6. 12. 18.]
[24. 30. 36.]
[42. 48. 54.]]
input
[[0.1 0.3 0.5]
[0.7 0.9 1.1]
[1.3 1.5 1.7]]
[[0.2 0.4 0.6]
[0.8 1. 1.2]
[1.4 1.6 1.8]]
output
[[598.5]]
[[615.6]]
[[632.7]]
多入力・出力の場合も、Conv2Dが何をやっているのかをこれで理解することができました。チャンネル数が1024になろうが、2048になろうが、図で書くのが難しくなるだけでやっていることは変わりません。
DepthwiseConv2D
ここからは特殊な畳み込みです。通常のConv2Dでだいたい事足りるのですが、精度が欲しかったり、パラメーター数(≒計算量)を減らしたかったりすると特殊な畳み込みが必要になることがあります。MobileNetで使われているDepthwiseConv2Dを見てみましょう。
KerasでのDepthwiseConv2Dの引数ですが英語版のドキュメントには書いてあり
keras.layers.DepthwiseConv2D(kernel_size, strides=(1, 1), padding='valid', depth_multiplier=1, data_format=None, activation=None, use_bias=True, depthwise_initializer='glorot_uniform', bias_initializer='zeros', depthwise_regularizer=None, bias_regularizer=None, activity_regularizer=None, depthwise_constraint=None, bias_constraint=None)
第一引数はチャンネル数ではなく、カーネルサイズになります。DepthwiseConvでは出力チャンネル数は入力チャンネル数と等しくなります。出力チャンネル数を変えたい場合は、Conv2Dや後述のSeparableConv2Dを使います。
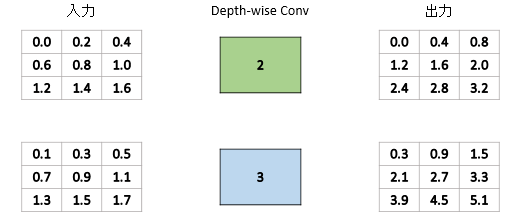
具体例を見てみましょう。DepthwiseConvというといかつく聞こえますが、カーネルサイズが1の場合はただ入力を定数倍しているだけです。作用は通常の畳み込みと同じく$X,Y$方向です。
Conv2Dのカーネルサイズ1(いわゆる1×1畳み込み)との大きな違いは、入力チャンネル数が$N$で出力チャンネル数が$M$, $N=M$のとき、1×1畳み込みではフィルター数は$N^2$個存在しますが、DepthwiseConv2Dの場合はフィルター数は$N個$しかありません。したがって、パラメーターと計算量は1x1畳み込みよりも更に減ります(ただしこれは表現力とトレードオフになります)。
カーネルサイズが2以上になった場合はこれに畳み込み処理が入ります。
from keras.layers import Input, DepthwiseConv2D
from keras.models import Model
import numpy as np
def depthwise_two():
input = Input((3,3,2))
layer = DepthwiseConv2D(3, use_bias=False)
x = layer(input)
model = Model(input, x)
weights = layer.get_weights()
print(weights[0].shape)#(3,3,2,1)
weights = np.arange(1,19).reshape(3,3,2,1).astype(np.float32)
layer.set_weights([weights])
print("weights")
print(weights[:,:,0,0])
print(weights[:,:,1,0])
X = np.arange(1,19).reshape(1,3,3,2) * 0.1
print("input")
print(X[0,:,:,0])
print(X[0,:,:,1])
result = model.predict(X)
print("output")
print(result[0,:,:,0])
print(result[0,:,:,1])
if __name__ == "__main__":
depthwise_two()
weights
[[ 1. 3. 5.]
[ 7. 9. 11.]
[13. 15. 17.]]
[[ 2. 4. 6.]
[ 8. 10. 12.]
[14. 16. 18.]]
input
[[0.1 0.3 0.5]
[0.7 0.9 1.1]
[1.3 1.5 1.7]]
[[0.2 0.4 0.6]
[0.8 1. 1.2]
[1.4 1.6 1.8]]
output
[[96.9]]
[[114.]]
実際、Excelなどで0.1×1+0.3×3+……+1.7×17を計算すると96.9になります。Conv2Dの多入力・多出力の場合のフィルター間の集約を捨てた形になっていますね。
SeparableConv2D
SepearbleConv2DはDepthwiseConv2DとConv2Dの合わせ技です。Kerasのドキュメントによると、
separable畳み込み演算は,depthwiseの空間的な畳み込み(各入力チャネルに別々に作用する)を実行し,続いてpointwiseに畳み込みを行い,両者の出力チャネルを混合します.
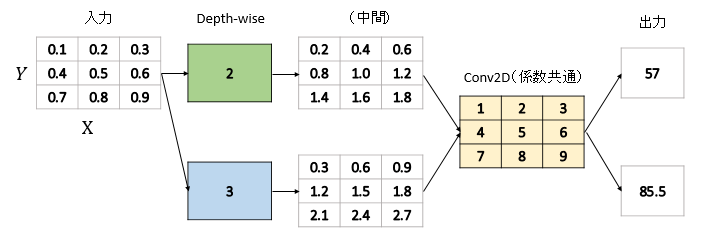
とあります。これはKerasの作者が作ったCNN、Xceptionで多用されているレイヤーです。簡単な例で示すと次のようになります。
このようにDepthwise($C$方向)と、Pointwise($XY$方向)で別々に独立のパラメーターを持っているのが特徴です。通常のConv2Dだったら、3×3行列のカーネルが2つあることになりますが、$C$方向は1×1の行列が2個、$XY$方向は3×3行列が1個で済んでいます。これはチャンネル数が大きくなったときに、特にパラメーター数で大きな削減効果2があります。
しかしこれらの演算はConv2Dでも内生的に表現でき、例えばConv2Dだったら、1番目のフィルターを2の倍数、2番目のフィルターを3の倍数にすれば同じ表現はできます。逆に言えば、SeparableConvとは$XY$方向と$C$方向が独立であるという仮定を置くことで、その対価としてパラメーター数の削減効果が得られるということになります。文字通り「Separable(分離可能)」というわけです。
ちなみにKerasでSeparableの計算結果を確認すると次のようになります。
from keras.layers import SeparableConv2D, Input
from keras.models import Model
import numpy as np
def separable_conv2d():
input = Input((3,3,1))
layer = SeparableConv2D(2, kernel_size=3, use_bias=False)
x = layer(input)
model = Model(input, x)
weights = layer.get_weights()
print(weights[0].shape)#(3,3,1,1)
print(weights[1].shape)#(1,1,1,2)
weights_xy = np.arange(1,10).reshape(3,3,1,1)
weights_c = np.arange(2,4).reshape(1,1,1,2)
layer.set_weights([weights_xy, weights_c])
print("weights xy")
print(weights_xy[:,:,0,0])
print("weights c")
print(weights_c[:,:,:,0])
print(weights_c[:,:,:,1])
X = np.arange(1,10).reshape(1,3,3,1) * 0.1
print("input")
print(X[0,:,:,0])
result = model.predict(X)
print("output")
print(result[0,:,:,0])
print(result[0,:,:,1])
if __name__ == "__main__":
separable_conv2d()
(3, 3, 1, 1)
(1, 1, 1, 2)
weights xy
[[1 2 3]
[4 5 6]
[7 8 9]]
weights c
[[[2]]]
[[[3]]]
input
[[0.1 0.2 0.3]
[0.4 0.5 0.6]
[0.7 0.8 0.9]]
output
[[57.]]
[[85.5]]
1つのレイヤーにつき、$XY$方向と$C$方向の係数を2つ持っているのが確認できます。
後ほど確認しますが、DepthwiseConvはあまりにパラメーター数が少ないのでそれ単体ではなかなか精度が出ません。しかし、SeparableConvは簡略化はされてはいるもののConv2Dの要素はあるので、Conv2Dよりは単体での精度は落ちるものの、DepthwiseConvほど精度は劣化しません。SeparableConvもDepthwiseConvも単体精度はConv2Dより劣るものの、パラメーター数が少ないゆえに重ねやすいので、「単体での精度が低くても、数を重ねればConv2Dだけより精度が上回る」のを狙ったものです。
Conv2DTranspose
せっかくなのでConv2Dの逆変換であるConv2DTransposeも見ておきましょう。普段は畳み込みの内容よりも、アップサンプリングの代用やデコーダー側のモデルで使うことが多いです。
Conv2Dの多入力・多出力の例と逆で、入力チャンネル$N=3$、出力チャンネル$M=2$とします。
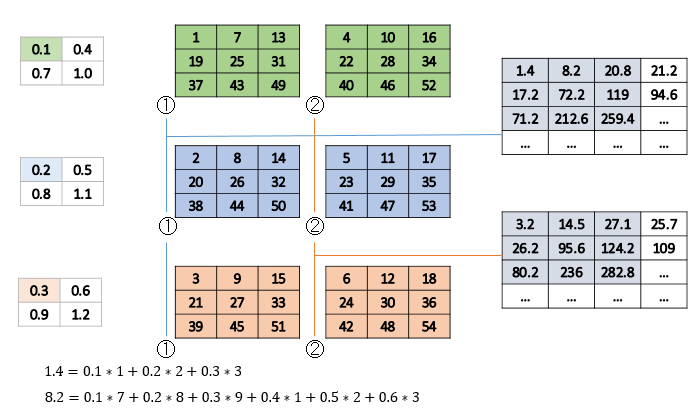
言葉で説明するのが難しいですが、出力の中央のセルほど作用するカーネル和が多くなるので複雑な計算式になります。出力の四辺の角のセルは作用するカーネル和が1つなので、ただのElementwiseの積の和となります。例えば、出力の1チャンネル目の左上の1.4は、「0.11+0.22+0.3*3」で求めています。その右隣の8.2になると、入力の左上のセル(0.1, 0.2, 0.3)からの作用と、入力の右上のセル(0.4, 0.5, 0.6)からの作用の和になるので、計6個の積の和になります。中央のセルはもっと複雑な式になります。
直感的には出力に係数の畳み込みカーネルを書けると入力になる。つまり、Conv2DTransposeは文字通りConv2Dの逆変換であると覚えておくのがいいと思います。
Kerasで確認する場合はそこまで難しくなくて、今までどおりにやればOKです。
from keras.layers import Conv2DTranspose, Input
from keras.models import Model
import numpy as np
def conv_transpose():
input = Input((2,2,3))
layer = Conv2DTranspose(2, kernel_size=3, use_bias=False)
x = layer(input)
model = Model(input, x)
weights = layer.get_weights()
print(weights[0].shape)#(3,3,2,3)
weights = np.arange(1, 55).reshape(3,3,2,3).astype(np.float32)
layer.set_weights([weights])
print("weights")
print(weights[:,:,0,0])
print(weights[:,:,0,1])
print(weights[:,:,0,2])
print(weights[:,:,1,0])
print(weights[:,:,1,1])
print(weights[:,:,1,2])
X = np.arange(1,13).reshape(1,2,2,3) * 0.1
print("input")
print(X[0,:,:,0])
print(X[0,:,:,1])
print(X[0,:,:,2])
result = model.predict(X)
print("output")
print(result[0,:,:,0])
print(result[0,:,:,1])
if __name__ == "__main__":
conv_transpose()
(3, 3, 2, 3)
weights
[[ 1. 7. 13.]
[19. 25. 31.]
[37. 43. 49.]]
[[ 2. 8. 14.]
[20. 26. 32.]
[38. 44. 50.]]
[[ 3. 9. 15.]
[21. 27. 33.]
[39. 45. 51.]]
[[ 4. 10. 16.]
[22. 28. 34.]
[40. 46. 52.]]
[[ 5. 11. 17.]
[23. 29. 35.]
[41. 47. 53.]]
[[ 6. 12. 18.]
[24. 30. 36.]
[42. 48. 54.]]
input
[[0.1 0.4]
[0.7 1. ]]
[[0.2 0.5]
[0.8 1.1]]
[[0.3 0.6]
[0.9 1.2]]
output
[[ 1.4000001 8.2 20.800001 21.2 ]
[ 17.2 72.200005 119. 94.600006 ]
[ 71.2 212.6 259.40002 181. ]
[ 91.399994 231.40001 265.6 165.2 ]]
[[ 3.2 14.5 27.1 25.7 ]
[ 26.2 95.600006 142.4 109. ]
[ 80.2 236.00002 282.8 195.4 ]
[ 98.6 248.5 282.7 175.1 ]]
こうなります。なんとなく見えてきましたよね。より厳密な定義を知りたい方はこちらの論文が参考になります(図がいっぱいあって読みやすい内容です)。
A guide to convolution arithmetic for deep learning
https://arxiv.org/abs/1603.07285v1
Conv2D, DepthwiseConv2D, SeparableConv2Dの精度の比較
画像認識(エンコーダー)で使う畳み込みレイヤー3種3の精度の比較をしてみます。CIFAR-10で比較します。
このように、「Conv2Dだけ、DepthwiseConv2Dだけ、SeparableConv2Dだけ」の10層のモデルを計3パターン作ります。正確にはどのケースでも、Poolingの後に1x1のConv2Dを入れていますが、これはDepthwiseConv2Dがチャンネル数を増やすことができないための調整措置です。
def create_block(mode, input, ch):
if mode == 0:
x = Conv2D(ch, 3, padding="same")(input)
x = BatchNormalization()(x)
x = Activation("relu")(x)
x = Conv2D(ch, 3, padding="same")(x)
x = BatchNormalization()(x)
return Activation("relu")(x)
elif mode == 1:
x = DepthwiseConv2D(3, padding="same")(input)
x = BatchNormalization()(x)
x = Activation("relu")(x)
x = DepthwiseConv2D(3, padding="same")(x)
x = BatchNormalization()(x)
return Activation("relu")(x)
elif mode == 2:
x = SeparableConv2D(ch, 3, padding="same")(input)
x = BatchNormalization()(x)
x = Activation("relu")(x)
x = SeparableConv2D(ch, 3, padding="same")(x)
x = BatchNormalization()(x)
return Activation("relu")(x)
def create_adjusting_block(input, ch):
x = Conv2D(ch, 1)(input)
x = BatchNormalization()(x)
return Activation("relu")(x)
def create_model(mode):
input = Input((32,32,3))
x = create_adjusting_block(input, 64) # Depthwiseの調整用
x = create_block(mode, x, 64)
x = AveragePooling2D(2)(x)
x = create_adjusting_block(x, 128) # Depthwiseの調整用
x = create_block(mode, x, 128)
x = AveragePooling2D(2)(x)
x = create_adjusting_block(x, 256) # Depthwiseの調整用
x = create_block(mode, x, 256)
x = GlobalAveragePooling2D()(x)
x = Dense(10, activation="softmax")(x)
model = Model(input, x)
return model
全体のコードはこちら。GPUで訓練させます。係数はレイヤーのタイプによって相当変わり、
| レイヤー | 係数 |
|---|---|
| Conv2D | 1,598,730 |
| DepthwiseConv2D | 58,506 |
| SeparableConv2D | 230,538 |
Depthwiseが異様に係数少ないですがこんなので大丈夫でしょうか。SeparableはXY方向とC方向に独立の仮定をおいているので係数の多さは中間という感じですね。テスト精度は以下のようになりました。
| レイヤー | テスト精度 |
|---|---|
| Conv2D | 87.66% |
| DepthwiseConv2D | 77.36% |
| SeparableConv2D | 84.33% |
Conv2Dはパラメーターが多いから精度が高いのは当たり前として、DepthwiseConvはパラメーターが1/30近くになっている割にかなり健闘していると思います。しかし、DepthwiseConvだけではまだまだ表現力が足りないので、他のレイヤーと組み合わせて使っていくのが大事だと思われます。事実、MobileNetはConv2DとDepthwiseConv2Dを織り交ぜた形式になっています。
Conv2Dより若干精度は落ちるものの、パラメーターの少なさと精度のバランスが良いのがSeparableConv2Dです。Xceptionの実装を見ると、畳み込みレイヤーの大部分がSeparableConv2Dで構成されています。単体でもこの精度が出るのなら、うまく組み合わせればSeparableConv中心でもネットワークとして成立すると思われます。
Optunaで最適な構成を調べる
せっかくなので、Optunaを使ってネットワークのブロック構成を探索します。どのレイヤーを使うのかというのは、立派なハイパーパラメータ探索です。モジュールは以下のように定義します。
環境:Optuna 0.5.0
- 1x1Conv2Dでチャンネル数の調整
- 「Conv2D」or「DepthwiseConv2D」or「SeparableConv2D」 1レイヤー目
- 「Conv2D」or「DepthwiseConv2D」or「SeparableConv2D」 2レイヤー目
- 「Conv2D」or「DepthwiseConv2D」or「SeparableConv2D」 3レイヤー目
- AveragePooling / GlobalAveragePooling (レイヤーに合わせてなのでチューニングしない)
これを1モジュールとし、先程の例と同様にPoolingをはさみながら3モジュール作ります。各Convの間にはBatchNormとReLUをはさみます。モジュール間でレイヤー構成は共通とします。つまり、3の3乗、27通りの組み合わせがあります。このぐらいだとOptuna使わなくてもグリッドサーチで探索できてしまいますが、Optunaを使ってほうがいい感じに枝刈りしてくれて楽なので、Optunaで探索させます。
100エポックを1試行とし、Optunaで50回試行させます。ただかなり枝刈りが入るので実際に5000エポック訓練することはなく、ColabのTPUで4,5時間程度で終わります(GPUだと時間かかって大変なのでバッチサイズを大きくしてTPUにしました)。
精度だけで見る場合
Optunaの目的関数を「テストデータのエラー率(1-精度)」とした場合です。これは確かめるまでもなく、「Conv2D→Conv2D→Conv2D」が明らかに良さそうです。ちなみにOptunaも同じ答えを返しました。
| ベスト | レイヤー1 | レイヤー2 | レイヤー3 | テスト精度 |
|---|---|---|---|---|
| 1 | conv | conv | conv | 88.46% |
| 2 | separable | conv | conv | 85.33% |
| 3 | separable | conv | conv | 85.06% |
| 4 | conv | depthwise | separable | 84.33% |
| 5 | depthwise | conv | separable | 83.95% |
3連Conv2Dが一番精度がよくて、Separable→Conv2D→Conv2Dも悪くないみたいですね。50試行のうち完走したのは6試行だけでした。
パラメーター数をペナルティーとして最適化
これだけでは面白くないので、パラメーター数が多いモデルにペナルティーを入れます。具体的には、model.get_prams()で総パラメーター数を取得し、
n_params = model.count_params()
パラメーター数25万につきエラー率5%相当のペナルティーを入れます。つまり、パラメーター数が100万ならテスト精度で20%マイナスするものとして考えます。かなりきつめのペナルティーを入れたのでこの設定はいろいろ変えて試してみると面白いと思います。
return 1.0 - max(history["val_acc"]) + (n_params / 250000 * 0.05) # 1Mのモデルは20%のペナルティー
こうすると3連Conv2Dはトップにこないかと思われます。全体コードはこちらにあります。他の設定は精度だけで最適化する場合と変わりません。コードを前の例とで使いまわしたせいで、枝刈りの部分での判定にパラメーター数を入れるのを忘れてしまいましたが、入れたほうが正確な枝刈りができるかもしれません。
| ベスト | レイヤー1 | レイヤー2 | レイヤー3 | 評価値 | パラメーター数 | テスト精度 |
|---|---|---|---|---|---|---|
| 1 | separable | separable | depthwise | 0.2407 | 236,810 | 80.67% |
| 2 | separable | separable | separable | 0.2598 | 322,826 | 80.48% |
| 3 | conv | depthwise | depthwise | 0.3283 | 834,890 | 83.87% |
| 4 | conv | separable | separable | 0.3586 | 1,006,922 | 84.28% |
| 5 | conv | separable | separable | 0.3590 | 1,006,922 | 84.24% |
今回Optunaは50試行中、10試行完走しました。それの評価値上位5件です。パラメーター数のペナルティーを入れたエラー率で評価したので、必ずしも順位が精度と連動していないのに注意してください。
パラメーター数25万につき精度5%相当というかなり高めのペナルティーなので、パラメーターが少ないモデルのほうが上位にきやすくなっています。しかし、パラメーター数が少なければいいという話でもなくて、3連DepthwiseConv2Dは理論上最もパラメーター数が少なくなりますが、Optuna的には試してすらいない、アウトオブ眼中という感じでした。
モジュール内でDepthwiseConvを2回やった例は2ケースほど完走していて、「Conv→Depthwise→Depthwise」はテスト精度が83.87%、「Depthwise→Depthwise→Conv」はテスト精度が78.55%でした(7位だったので上の表には出ていません)。Depthwiseを多く使う例は、Depthwiseの数よりもConvとの位置関係でかなり精度が変わるというのが面白いですね。ちなみにMobileNetはDepthwiseよりもConvを先に入れているので、確かにOptunaでもこのアーキテクチャが答えとして再現されています。
結局、パラメーター数を加味して調整すると、XceptionのようなSeparableConvが中心の例が強くなるそうです。また、MobileNetのようなConv→Depthwise→Depthwiseのようなケースも良かったです。この結果はパラメーター数のペナルティーにかなり依存するので、本格的に試したいのならいろいろ設定を変えてやってみるのをおすすめします。また、パラメーター数ではなく、推論時間や訓練時間をペナルティーとするとかなり実践的なモデルチューニングができて面白いと思います。YOLOだったら推論のFPSが問題になることが多いですので。
まとめ
若干長くなってしまいましたが、Conv2D、DepthwiseConv2D、SeparableConv2D、Conv2DTransposeは次のような違いがあります。
- Conv2D:入力の出力でチャンネルでカーネルを総当たりで試す。パラメーター数が多い分最も精度が出やすい
- DepthwiseConv2D:チャンネル方向に独立な畳み込みを行う。パラメーター数はすごく減るが、単体ではなかなか精度が出ない。MobileNetで使われているように、Conv→DepthwiseConvと併用すると結構使える。
- SeparableConv2D:$XY$方向と$C$方向に独立の畳み込みを行う。パラメーター数はDepthwiseConv2D以上Conv2D未満で、精度もそのような形になる。パラメーター数を減らす分モデルを深くしやすい。XceptionのようにSeparableConv2D中心のネットワークでもかなり戦える。
- Conv2DTrasnpose:文字通りConv2Dの逆変換。エンコーダーで使うことはなく上の3つとはかなり毛色が違うが、具体的な計算の流れを確認することができた。
また、Optunaを使ってモジュール構成を調べた所、MobileNetの構成や、Xceptionの構成がパラメーター数をへらすという点と、精度の両立という点ではかなり理にかなっているということもわかりました。こんなところです。今までなんとなくわかっていてモヤモヤしていたところがはっきりしてスッキリしましたし、Optuna面白いですね。
-
特にSVMに見られるような「カーネルトリック」に近いアルゴリズムを使う場合は、バッチ間の演算が必要になります。例えばニューラルネットワークでクラスタリングしたり、サンプル間の距離を考えるような埋め込み計算をしたい場合はバッチ間の計算を定義することがあります。若干面倒なので今回は考えません。 ↩
-
計算量の削減効果については確実にあるとはいえません。なぜならXY方向は係数を使いまわししているだけで、実質的な畳込み回数はチャンネル数の2乗のオーダーから、定数倍のオーダーに変わっただけだからです。チャンネル数が多いような状態では計算量の削減効果は大きいですが、チャンネル数が小さいような場合はだと処理時間を計測したときに逆に遅くなっていたなんてこともあります。 ↩
-
Conv2DTrasposeをエンコーダーで使うことはまずないので除外します ↩