2021年のディープラーニング論文を1人で読むAdvent Calendar20日目の記事です。今日読むのは「ディープラーニングベースの株式市場のポートフォリオ理論」の論文です。これまで画像処理の論文が中心でしたが、今回は時系列データです。著者は日本人で、PFNと野村アセットマネジメントの方です。AAAI2021に採択されています。
この論文、実は日本語版があります。英語版がAAAI2021、日本語版が人工知能学会の研究会で使われたものです。自分は最初日本語版ないと勘違いしていて、英語版をやっとの思いで読み終わったら「日本語版ある!しかもめっちゃ綺麗にまとまってる。自分解説する必要なくないですか?」と悲しみを背負ったので、最初は日本語版でアウトラインをつかむことをおすすめします。ネットワーク構造等は英語版(arXiv)のAppendixに載っています。
最初に断っておきますが、この論文かなり難しくほぼほぼ線形代数の内容です。本文はまだギリギリついていけたのですが、証明になったら白目剥いたんで飛ばしました。コードがなく、かなり自分の憶測で読んでいる部分がありますのでご注意ください。投資は自己責任で。自分はこの論文に対してやや懐疑的な見方をしています。そういうのが苦手な方はブラウザバックしてください。
- タイトル:Deep Portfolio Optimization via Distributional Prediction of Residual Factors
- URL:https://ojs.aaai.org/index.php/AAAI/article/view/16095
- 出典:Imajo, K., Minami, K., Ito, K., & Nakagawa, K. (2021). Deep Portfolio Optimization via Distributional Prediction of Residual Factors. Proceedings of the AAAI Conference on Artificial Intelligence, 35(1), 213-222. Retrieved from https://ojs.aaai.org/index.php/AAAI/article/view/16095
- arXiv:https://arxiv.org/abs/2012.07245
- 日本語版:https://sigfin.org/?plugin=attach&refer=026-05&openfile=05_SIG-FIN-26.pdf
CAPMとファーマ-フレンチモデル
本論文に行く前に、古典的な資産価格モデルを紹介しましょう。株式の変動(収益率)をデータを使って説明しようとする試みは相当昔からあり、ディープラーニングよりも全然歴史が古いです。最も有名なのがウィリアム・シャープらによって1960年代に発表された**CAPM(Capital Asset Pricing Model)**です。
株式の収益率
CAPMに行く前に株式の収益率について定義しましょう。$i\in{1, \cdots, S}$番目の株式の時点$t$における価格(株価)を$p_{i, t}$とします。収益率を$r_{i,t}$は、
$$r_{i, t} = \frac{p_{i, t+1}}{p_{i, t}}-1$$
で表されます。例えば今日の株価が1000円で、翌日の株価が1050円なら収益率は5%。翌日の株価が950円なら収益率は-5%となります。
CAPM
CAPMでは株式の収益率を、市場ポートフォリオの収益率を用いて説明します。市場ポートフォリオは現実的な分析では、株式インデックス(例:日経平均やTOPIX、SP500)を用いて代用します。株式の期待収益率を$r_i$, 市場ポートフォリオの期待収益率を$r_M$とします。ここで国債のレートをリスクフリーレートとして$r_f$とすると、
$$r_i-r_f=\beta_i(r_M-r_f)$$
で説明できるとするのがCAPMです。株式の収益率、市場ポートフォリオの収益率ともにリスクフリーレートで引いています。2021年現在は鼻くそみたいなゼロ金利なのであまり気にすることはないのですが、60年代は相当金利が高かったので問題になったのでしょう。
これは統計風に見れば、株式インデックス(市場ポートフォリオ)による単回帰分析と捉えることもできます。ただ、単回帰だとそんなに精度出ないですよね。。これよりもう少し凝ったモデルがファーマ-フレンチの3ファクターモデルです。
ファーマ-フレンチの3ファクターモデル
ファーマ-フレンチの3ファクターモデルは、1993年にユージン・ファーマとケネス・フレンチによって発表されたモデルです。説明変数が3つに拡張されています。
$$r_i-r_f=\beta_i^{MKT}(r_M-r_f)+\beta_i^{SMB}SMB+\beta_i^{HML}HML$$
$SMB$は時価総額に対するリスクファクター、$HML$は簿価時価比率(PBRの逆数)に対するリスクファクターです。$\beta_i^*$は各パラメーターに対する係数です。
データサイエンスが普及しまくった今から見れば「なーんだ、特徴量追加して重回帰にしただけやん。俺でもできるわ(鼻ホジ)」と思ってしまいますが、CAPMのウィリアム・シャープは1990年に、ファーマフレンチのユージン・ファーマは2013年にノーベル経済学賞を受賞しています。回帰分析をすればノーベル賞を取れる時代があったのです。
アルファがない?
CAPMもファーマフレンチも回帰分析に対する切片がないのに気づきます。回帰分析的にはこう表現するほうが自然でしょう。
$$r_i-r_f=\sum_{k=1}^K\beta_i^{(k)}f^{(k)}+\alpha_i$$
$K=3, \alpha_i=0$とすればファーマ-フレンチのモデルになります。CAPMもファーマフレンチも$\alpha_i=0$としています。これは効率的市場仮説と関連していて、「情報が即時に織り込まれるから、ミスプライスは起こらない。仮にアルファがあったとしても、人々がその差を求めてすぐに取引するから最終的に0になる」という、まあ絵に描いた餅の理論です。
最初に断っておきますと、本論文は「アルファはある」というスタンスです。むしろ「マーケットに連動するような要因(狭義の例では、マーケットに連動するβ)を排除して、アルファの部分をいい感じに予測し、ポートフォリオを調整することでコンスタントに収益を狙っていこうね」というスタンスなので、裁定取引とみなすことができます。
本論文の基本的な資産価格モデル
本論文では銘柄$i$時点$t$の収益率$r_{i, t}$を次のように表現します。
$$r_{i_t}=\sum_{k=1}^K\beta_i^{(k)}f^{(k)}+\epsilon_{i, t}$$
$\beta$は株式インデックスのような銘柄間で共通の要因、$\epsilon$がそれらの要因を除外した個別銘柄の要因です。本論文では$\epsilon$を**残差項(Residual Factors)**と呼んでいます。本論文の目的は残差項$\epsilon$の予測です。
もしCAPMの世界だったら、残差項=リスクフリーレートとなってしまうため、予測する必要がありません。この論文は「アルファはある」というスタンスであると捉えることができます。
スペクトルによる残差項の抽出
この論文での大きな目的は、株式インデックスのような銘柄間の共通の要因を除外することです。これは**特異値分解(主成分分析)**でできます。具体的には株式の収益率の行列を特異値分解をしたあと、特異値の大きな成分をマスク(=0)とします。これで行列積を再度計算したものが、残差項(Residual Factors)$\boldsymbol{\tilde{\epsilon}}_s$です。
定式化
残差項を求めるところまでを定式化しましょう。収益率のデータを$H$個の窓でとった値を$\boldsymbol{X}_t:=[\boldsymbol{r}_{t-H}, \cdots, \boldsymbol{r}_{t-1}]$とします。ここで$\boldsymbol{X}_t$は$S\times H$の行列です($S$は銘柄数です)。
$\boldsymbol{X}_t$の特異値分解の結果は次のようになります。
$$\tilde{\boldsymbol{X}}_t=\boldsymbol{V}_t\rm{diag}(\sigma_1, \cdots, \sigma_S)\boldsymbol{U}_t$$
ここで$\boldsymbol{V}_t$が$S\times S$の直交行列、$\boldsymbol{U}_t$が$S\times H$で各行は互いに直行な単位ベクトルを表します。$\sigma_1\geq \cdots\geq\sigma_S$が特異値で、特異値は大きい順に並んでいるものとします。特異値分解はnp.linalg.svdでできます。
ここから特異値を大きい順に$C$個マスクし、$\boldsymbol{A}_t$を次のように定義します。$C$はハイパーパラメータになります。
\boldsymbol{A}_t:=\boldsymbol{V}_t\rm{diag}(\underbrace{0, \cdots, 0}_{C}, \underbrace{1, \cdots, 1}_{S-C})\boldsymbol{V}_t^T
時点$s(t-H\leq s\leq t-1)$のスペクトル残差(残差項)$\tilde{\boldsymbol{\epsilon}_s}$を次のように定義します。
$$\tilde{\boldsymbol{\epsilon}_s}:=\boldsymbol{A}_t\boldsymbol{r}_s$$
ここで$\boldsymbol{r}_s$は時点$s$の収益率のベクトルを表します。
ネットワークの対する2つの要件
最終的には将来の残差項目(の分布)をニューラルネットワークで予測するのですが、株式の収益率をモデリングするにあたり2つの要件が必要になります。1つはボラティリティ不変性、時間軸不変性です。
ボラティリティ不変性
ボラティリティとは株価の変動のことで、株価の収益率の標準偏差で観測することが多いです。例えば、リーマンショックのような大きなクラッシュがあったときは乱高下しますし、穏やかな上昇相場のときは値幅はより小さくなる傾向になります。ボラティリティは一定の継続傾向があり、ボラティリティが大きいときはしばらく大きい状態が続き、ボラティリティが小さいときは小さい状態が続く傾向があります(ボラティリティ・クラスタリングと呼ばれています)。
ボラティリティが小さいときでも、大きいときでも「金融時系列らしさ」というのはそれほど変わらないわけで、ボラティリティが小さいケースに定数倍したら、ボラティリティが大きいケースになるようにしたいのです。数学的には、**ニューラルネットワークが正の同次関数(positive homogeneous function)**となるような保証をします。同次関数とは$f:\mathbb{R}^n\to\mathbb{R}^m$において、$f(a\boldsymbol{x})=af(\boldsymbol{x}), \boldsymbol{x}\in\mathbb{R}^n, a>0$となる関数です。
具体的には、任意の関数を$\tilde{\psi}$としたとき、
$$\psi(\boldsymbol{x})=|\boldsymbol{x}|\tilde{\psi}\Bigl(\frac{\boldsymbol{x}}{|\boldsymbol{x}|}\Bigr)$$
となるようにします。実装上は、後述のフラクタルネットワークの入力・出力を、この式で前処理+後処理します。定量評価的にはこのボラティリティの正規化がかなり重要になります。
※論文読んだ限りでは、ボラティリティの正規化、フラクタルネットワークの「Rescaling」の二種類の正規化があり、混同してしまいましたが、著者に教えていただきました。ありがとうございました。
時間軸不変性(フラクタル性)
株価の時系列にはフラクタル構造を持つという有名な仮説があるそうです。このフラクタル性を取り入れたいのです。ただこれはネットワーク構造やサンプリングで表現できます。フラクタルネットワークを導入します。
やっていることは単純で、累積した収益率をランダムに異なる大きさのウィンドウで切り出して、一定の解像度へリサイズするだけです。画像の前処理でランダムな大きさのパッチを取ってリサイズするのと感覚的には似ています。異なるパッチでリサンプリングして、アンサンブルすることでフラクタル性を表現しています。式で表せば、
$$\psi(\boldsymbol{x})=\psi_2\Bigl(\frac{1}{L}\sum_{i=1}^L\psi_1(\rm{Resample}(\boldsymbol{x}, \tau_i))\Bigr)$$
となります。$\psi_1, \psi_2$という2つのネットワークからなります。$\psi_1$は複数のパッチによるパスを、重み共有のような形で表現するのでしょうね。$\psi_2$はアンサンブル結果から、将来の収益率の残差項の分布を求めるネットワークです(後述)。
分位点回帰による将来の分布予測
このモデルでは何を予測したいかというと、以下の条件付き分布の予測です。
p(\tilde{\epsilon}_{i, t}|\tilde{\epsilon}_{i, t-H}, \cdots, \tilde{\epsilon}_{i, t-1})
これは$t-1$までの残差項を条件として、$t$の残差項の分布の予測です。このモデルの面白いのは、将来の残差項を直接数値として推定するのではなく、分位点回帰(Quantile Regression)を使って分布ごと推定するという点です。
これは事前分布に正規分布をおいてベイズのアプローチをすれば解析的に解けますが、正規分布として仮定するのは良くないケースがあることがわかっています。例えば、マーケットクラッシュのときは正規分布から外れた値が連続し、分布が歪む(100年に一度という表現をリーマンのときによくしましたが、それが連続して出てくるようなイメージです)ことがわかっているので、分布を仮定しないノンパラメトリックなアプローチのほうがいいのです。従来の統計だとノンパラへの拡張が大変だったのですが、ディープラーニングだとこれは割と楽勝で、この論文では分位点回帰を使って推定しています。分位点回帰自体はSklearn等で容易にできます。
ピンボールロス
本論文のアーキテクチャでは$Q-1=31$個のクォンタイルとした、分位点回帰をします。「分位点回帰だからといって、例えばクォンタイルごとの確率値が必要になるのか」といったらそんなのことはなく、損失関数が変わるだけで回帰問題のままです。$\alpha\in(0, 1)$とし、$\alpha$がクォンタイルのインデックスを表すものとします。このとき分位点回帰の**ピンボールロス(Pinball loss)**は、
\mathcal{l}_\alpha(y, y'):=\max\{(\alpha-1)(y-y'), \alpha(y-y')\}
で定義されます。$y'$は教師データから与える値です。ここで$\boldsymbol{x}_t=(\tilde{\epsilon}_{i, t-H}, \cdots, \tilde{\epsilon}_{i, t-1})^T, y_t=\tilde{\epsilon}_{i, t}$です。
| α | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|
| y=0 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| y=20 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
実際に$y'=10$と固定して、$y=0, 20$で変えると、$\alpha$ごとのロスは上の表のようになります。$\alpha$は「○○%クォンタイル」をそのまま表しているので、もし推定値が真の値より小さければ($y=0$)、ボトム側のクォンタイルに強い勾配がかかるようになります。逆に推定値がが真の値より大きければ($y=20$)、トップ側のクォンタイルに強い勾配がかかるようになります。こうやってクォンタイルごとにロス(勾配)を変えることで分布を表現しようとしたのが、ピンボールロスです。
平均分散予測
最終的には将来の残差項(スペクトル残差)の平均分散を求めることで、ポートフォリオのウェイトが求められます。分位点回帰から平均$\hat{\mu}_t$分散$\hat{\sigma}_t^2$を求めるには次にようにします。
\hat{\mu}_t:=\hat{\mu}(\tilde{\boldsymbol{y}}_t)=\frac{1}{Q-1}\sum_{j=1}^{Q-1}\tilde{y_t}^{(j)} \\
\hat{\sigma}^2_t:=\hat{\sigma}^2(\tilde{\boldsymbol{y}_t})=\frac{1}{Q-1}\sum(\tilde{y}_t^{(j)}-\hat{\mu}_t)^2
ポートフォリオのウェイトを求めるには、平均を分散で割ればよく、銘柄$j$のポートフォリオのウェイト$\hat{b}_j$は、
\hat{b}_j:=\lambda^{-1}\frac{\hat{\mu}_{t,j}}{\hat{\sigma}^2_{t,j}}
ここで$\lambda$は投資家のリスク回避係数です(参考資料)。いきなり出てきましたが、古くからあるポートフォリオ理論の「平均分散モデル」に基づいています1。リスク回避係数は経済学における効用関数に出てくるパラメーターです。
ゼロ投資ポートフォリオ
この論文では**ゼロ投資ポートフォリオ(zero-investment portfolios)**を採用しています。つまり、買いのポジションと同数空売りポジションを持つということです。数式で表せば、
$$\sum_{i=1}^Sb_t^{(i)}=0$$
現実的にはポジション数をイコールにすることよりも、金額ベースでイコールにならないと意味がないような気がしますが、そこらへんは株価を正規化したりして調整するんでしょうかね。またポジションの和が常に1になるようにします。つまり、
$$\sum_{i=1}^S|b_t^{(i)}|=1$$
ここで$b_t^{(i)}$は時点$t$における$i$番目の銘柄の保有数です。プラスなら買い、マイナスなら空売りとなります。
ゼロ投資ポートフォリオを採用することによって、投資家のリスク回避係数を外せます。ゼロ投資ポートフォリオでの持ち分は、L1ノルムで割ることで求められます。
\frac{\boldsymbol{b}_t-\bar{b}_t}{\|\boldsymbol{b}_t-\bar{b}_t\|_1}, \qquad \bar{b}_t=\frac{1}{S}\sum_{j=1}^S b_{t,j}
ここで$\boldsymbol{b}_t$はベクトル、$\bar{b}_t$はスカラーを表します。
ネットワークのアーキテクチャ
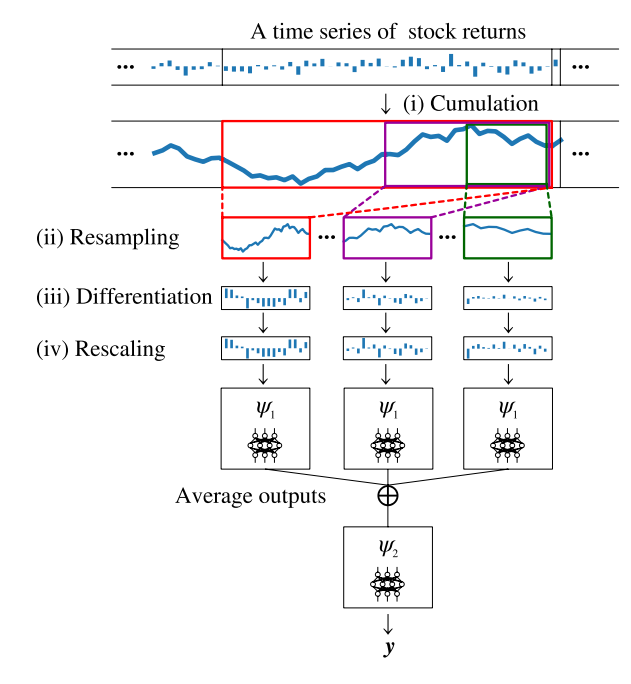
ここでフラクタルネットワークの詳細なアーキテクチャについて見てみましょう。これを見るとコードがなくても、実装像が見えてきます。
ネットワークには
- Cumulation
- Resampling
- Differentiation
- Rescaling
の4ステージがあります。
Cumulation
「A time series of stock returns」と書いてあるのは、特異値分解を適用しマーケット等の影響を取り除いた残差項(スペクトル残差)です。ボラティリティ不変性を保証するためにノルムで正規化する前処理をしています。これを$H$期取り、$\boldsymbol{x}=(x_1, \cdots, x_H)$とします。次に各期の累積和$\boldsymbol{z}=(x_1, x_1+x_2, \cdots, x_1+\cdots+x_H)$とします。
Resampling
まずはサイズの異なる窓でパッチを切り出します。切り出す範囲は、$z_{\lfloor(1-\tau)H\rfloor}, \cdots, z_H$となり、$\lceil\tau H\rceil$個の要素が含まれます。これを$H'$の固定長へとリサイズします。実装上は、画像のリサイズのように行うと思われます。
ハイパーパラメータ$\tau$は、$\tau_j:=4^{-j/20}, j\in{0, \cdots, 21}$としています。リサイズ後の固定長$H'=64$です。
Differentiation
ここでは累積和の特徴量だったので、さらに差分をとって、残差項へと戻します
Rescaling
$\tau^{-1/2}$で割ります。これは、ハースト指数$\mathcal{H}$を持つ分数ブラウン運動の場合、自己相似性からスケーリング係数が$\tau^{-\mathcal{H}}$だからです。多くの市場において$\mathcal{H}\approx 0.5$であることに基づいています。
ネットワークψ1
Rescalingの後に通すネットワーク$\phi_1:\mathbb{R}^{H'}\to\mathbb{R}^{K}, (K=256)$について。3層からなるMLPです。全ての層の出力チャンネルは256で、50%のドロップアウトと、BatchNormalizationが入っています。活性化関数はReLUを使っているとの記述がありましたが、どこに入れているかは明確にかかれていませんでした(多分BNの後に入れているのだと思います)。
このあと平均をとりアンサンブルしてネットワーク$\psi_2$へと続きます。
ネットワークψ2
$\phi_1:\mathbb{R}^{K}\to\mathbb{R}^{Q-1}, (Q-1=31)$8層からなるMLPです。最終層以外に出力チャンネルは128です。$psi_1$同様、50%のドロップアウトと、BatchNormalizationが入っています。 これで残差項のクォンタイルが求められました。
後処理
ネットワークの入力で、ボラティリティの不変性のための正規化をしていますが、出力時に後処理としてノルムを掛けて戻す操作をします。
数値実験
データ設定や実験設定
- アメリカのSP500に登録された銘柄のうち、2000年~2020年について取得
- 2000年から2008年までを訓練とValidation、残りをテストとした(注釈:時系列のTrain test splitは難しいので参考になる)
- 始値を基準に計算する。これはマーケットが開いたときのほうが取引量が多いから。金融機関が大引けで大量の取引をするのは「banging the close」という違法行為とみなされる可能性があるから2
- ポートフォリオのアップデートまで1日遅延するものと設定。
評価指標
- Cumulative Wealth(CW):ポートフォリオの収益率の累積和
- Annualized Return (AR):年率の収益率
- Annualized Volatility(AVOL):年率のボラティリティ
- Annualized Sharpe ratio(ASP):年率のシャープレシオ(年率の収益率÷年率のボラティリティ:高いほうが良い)
結果
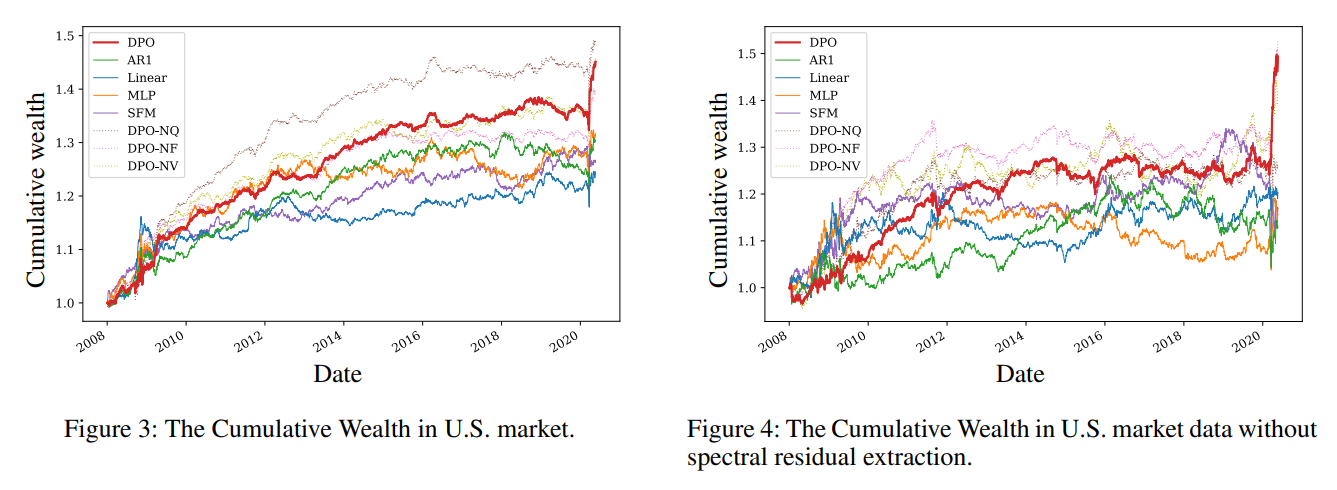
テストデータでの比較
まあまあ良さそうに見える。「AR(1)」という原始的なモデルと比べても、12年放置して10%ちょい変わるかどうかぐらいなんですね。
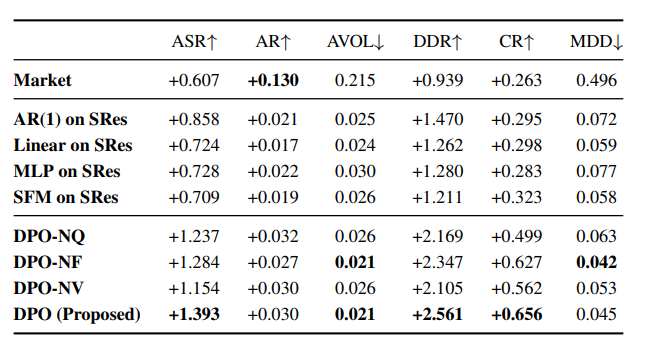
ここではいわゆる「Ablation studies」がやられていて、
-
DPO-NQ: 分位点回帰をやめて、L2ロスでただ回帰する -
DPO-NF:フラクタルネットワークをやめてシンプルなMLPにする -
DPO-NV:ボラティリティ不変性を保証するための正規化をやめる
「ASR」(年率シャープ比)基準で見れば、ボラティリティの不変性の保証が一番重要。次に分位点回帰、フラクタルネットワークの順。AVOLが下がった結果シャープ比が上がっている結果が多い。ボラティリティ不変性による正規化、分位点回帰による分布推定のようにボラティリティに対してアプローチするのは良さそう。
自分からの疑問
この論文、読んでいて珍しく「これおかしくない?」という点が見つかったので書いていきます。
実は年次リターンの大半がリスクフリーレートで説明できる
CAPMやファーマフレンチモデルでは、効率的市場仮説より、$\alpha=0$となります。
$$r_i-r_f=\beta_i(r_M-r_f)$$
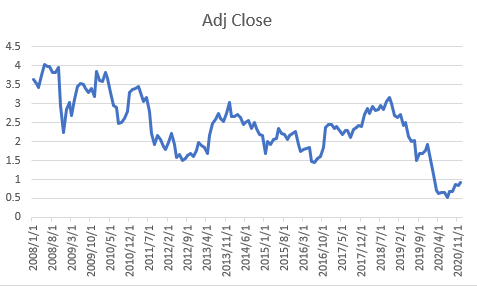
本論文で扱っている「残差項」はβの影響を限りなく落としたものであるので、$\hat{\epsilon}\approx r_f$となることが懸念されます。実際にこれは米国の例で計算しているので、米国のリスクフリーレートとして扱われることの多い「10年物国債」の利回りのデータをYahooファイナンスから月次で取ってきます。テストデータの対象期間である2008年~2020年をプロットします。
これらの系列の平均をとると、**2.34%**でした。提案手法より前の「MLP on SRes」はARが2.2%でしたので、国債のレートよりも悪いことが確認できます(投資しないほうがいいレベル)。提案手法は年率リターン3%でしたので、リターンのうち78%は国債利回りで説明できることがわかります。これはCAPMの通りの結論です。
本論文では収益率の計算時にリスクフリーレートを無視している(ゼロ投資ポートフォリオという理由)ので、結果ポートフォリオのリターンが国債利回りに近くなってしまうのはある意味当然と言えるでしょう。
取引コストを考えているかが不明
一方でテストデータの範囲内で、AR等の手法をアウトパフォームしているのは事実です。しかし、これが現実的な取引をシミュレートしているかは疑問があります。現実点との乖離は以下の通りです。
- 売値と買値のスプレッド
- 理論的には小数点となって計算できているが、取引単位量未満のポジションがあるために完全な「ゼロポートフォリオ戦略」が満たせないこと
- 完全な「ゼロポートフォリオ戦略」を特定のタイミングで満たせないことによる、リアロケーションの必要性
- ゼロポートフォリオ戦略が本当はロット数の和ではなく、評価額の和で考えるべきなこと(株価に対してどういう正規化をやっているか不明)
- 空売り禁止や逆日歩を無視している
- サーキットブレーカーや(日本なら値幅制限)があるため、始値で100%の取引を満たせるかはわからない
- 空売りをする際の担保率や担保率の変動による追証の可能性を無視している
- 市場内の銘柄の入れ替え(上場廃止や統合、新規上場)をどうするのか
もちろん全部をシミュレーションするのは難しいですが、シミュレーションに含まれていない取引コストが相当あると思われます。そう考えていくと、年間リターンの3%のうちリスクフリーレートを引いた「提案手法のゲインである0.66%」はすぐに消えてしまうのではないでしょうか。
なので、もっと現実的な取引のシミュレートをしたらあの通りには儲からないか、トントン~金利レベルで終わってしまうのではないかと思われます。結局は、伝統的なポートフォリオ理論が前提としている効率的な市場のように、「長期的に見たらアルファはほぼない」ということを皮肉にも裏付けてしまっている可能性はあります。ましてや特異値分解で相当主成分を抜いているため、残差項がリスクフリーレート+ノイズに回帰している可能性はかなりあります。
まとめと感想
この論文では、従来のポートフォリオ理論をディープラーニングベースに落とし込むことに成功しています。一方で、従来の経済学ベースでの古い理論も一緒に引き継いでいるようにも思えます。例えば、アルファを求めようとしているのに、ランダムウォークを前提とした理論展開をしているように見えるところ(例えば、ノイズによる回帰はランダムウォークを前提としているように見える)。あるいは伝統的なポートフォリオ理論の前提である、効率的な市場まで模倣しているように見えること。従来のポートフォリオ理論ベースでもそうでしたが、そういった自己矛盾を抱えてしまうのは致し方ないでしょうね。数学的にはめちゃくちゃ頑張っているのに、理論展開の戦略性が「ん?」と思ってしまうのは今後の課題かなと思われます。
ディープラーニングは数学的なモデルはさておき「何でもかんでもモデルに組み込んで、End-to-Endで回してしまう」というのはとにかく強いので、既存の経済理論にとらわれないでもっと柔軟なモデル作りが出てくると面白いなと思います。ただ、昔懐かしいポートフォリオ理論が現代の技術で焼き直し+αされているのを見れたのはなかなかおもしろいものがありました。
非常に難しい線形代数の話でしたが、論文内での次元や変数の注釈がかなりしっかり書かれていて、そこらへんがよくわからない人でも読みやすいように配慮されているのはとても良かったです。このスタンスはぜひ引き継いでほしいです。
告知
このアドベントカレンダーが本になりました!
https://koshian2.booth.pm/items/3595424
Amazonでも扱いあります詳しくは👉 https://shikoan.com