tl;dr
- 目的:なぜ簡単な問題においてパーセプトロンよりもSVMのほうが性能が良いことが多いのか、それは本当なのかを考察する。
- 特に、ラベルあたりのデータ数に偏りがある場合。
- SVM、単層パーセプトロン、SVMと同じ損失関数の単層パーセプトロンで振る舞いを比較した。
- 定性的な評価だが、SVMがもっともよかった。少なくとも損失関数の違いだけではないことがわかった。
- 最適化法の違い、パラメータの選び方が効いているのかもしれない。
はじめに
線形SVM1は歴史ある分類器ながら、その強力さから現代でも広く使われています。分類器としては近年ニューラルネットワーク、特にニューラルネットワークを多層にかさねた深層学習が話題になっています。しかし、これはあくまでも感覚なのですが、がんばって訓練したニューラルネットワークよりも素朴な線形分類器であるSVMのほうが性能が高いことが多々あります。
線形SVMとニューラルネットワークというのは、実はとても近い手法です。SVMの最適化対象を損失の形で書くと、
$$
L(x,y;W,b) = \frac{1}{2}||W||^2 + C\max(0, 1 - Wxt)^2
$$
ただし、$x$は入力の特徴量、$W$はモデルパラメータ2、 $t=\{-1,1\}$ はラベルです。損失の左項は、$W$に関する正則化項です。 $C$ はユーザパラメータで、SVMのコンテキストでは「マージン最大化と分類ミスを抑制するこのトレードオフ」のように説明されます3。式を見ればわかるように、Cとは結局正則化項の効き方をコントロールするパラメータで、ニューラルネットワークのコンテキストでは過学習を防ぐためにコントロールするパラメータとして理解されます。
上記式は、ヒンジ損失を採用した一層パーセプトロンと全く同じです4。では、実用上SVMとパーセプトロンは何が違うのでしょうか。パーセプトロンはSVMをより一般化した概念であり、通常、確率的勾配降下法や、その亜種によって最適化されます。確率的勾配降下法 (SGD) は一階(劣)微分可能な関数であれば何にでも適用できるので、現在の深層学習のように複数のパーセプトロンを重ねたようなものにでも適用できるメリットがあります。それに対してSVMでは一般性と計算スピードを犠牲にしてより高度な最適化法を使います。例えば、SVMの2大ライブラリであるLIBSVMでは二次計画法の一種であるSMOが、LIBLINEARでは共役勾配法が、それぞれ使われています。また、実装を実際にみたわけではないので予想ですが、初期化法などに様々なヒューリスティックが使われ、良い性能がだされるようにチューニングされていると考えられます。
本投稿では、損失関数は同一ながら、性能が違うSVMとパーセプトロンを、分類の可視化を通して比べてみたいと思います。
比較するアルゴリズム
SVM
SVMは sklearn.svm.SVC と sklearn.svm.LinearSVC の実装を使います。2つの実装は、それぞれバックエンドにLIBSVMと、LIVSVMを使っています。
パーセプトロン
パーセプトロンはChainerを使って実装しました。
linear = L.Linear(2)
y = linear(x)
loss = F.hinge(y, t, norm='L2')
学習にはモーメンタム付きSGDに、学習率のdecayを加えたもので、パラメータなどは感覚で決め打ちです。パラメータである$C$の値ですが、要は2つのパラメータ間の関係を維持できればよいので、下記のように変形し、WeightDecayのパラメータとして食わせました。
$$
\frac{1}{2}||W||^2 + C\max(0, 1 - Wxt)^2 \propto \frac{1}{2C}||W||^2 + \max(0, 1 - Wxt)^2
$$
また、工夫として、入力データのスケーリングと白色化を施しています。これをいれないとニューラルネットワークはまともにうまく学習できませんでした。
self._scaler = MinMaxScaler().fit(X)
X = self._scaler.transform(X)
self._whitener = PCA(whiten=True).fit(X)
X = self._whitener.transform(X)
実装と実験結果はGithubにアップロードしてあります。
結果
普通のデータ
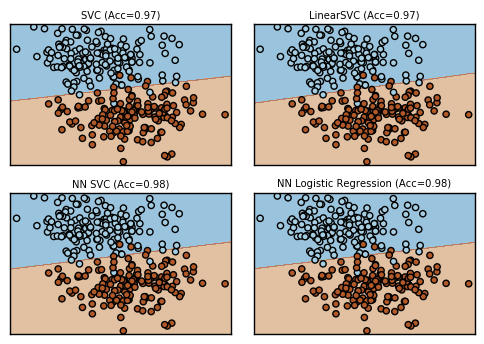
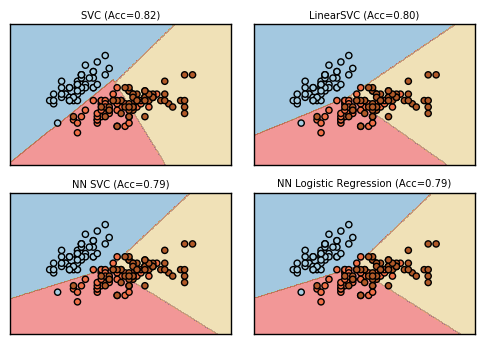
NN SVCがパーセプトロンにヒンジ損失をいれたものです。参考まで、NN Logistic Regressionとなっているのは通常のsoftmax cross entropy損失です。
このくらいのデータだとどのアルゴリズムも十分よく分類できています。
アンバランスなデータ
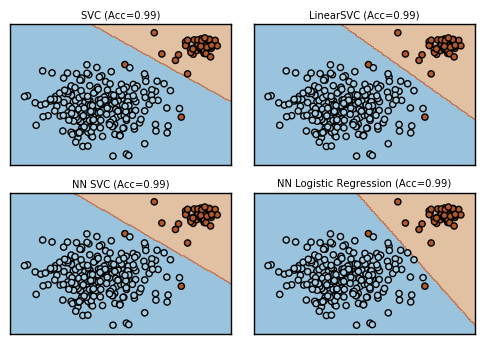
少しラベルあたりのデータの数を偏らせてみました。このくらいならば、まだまだどのアルゴリズムも楽勝といったところです。
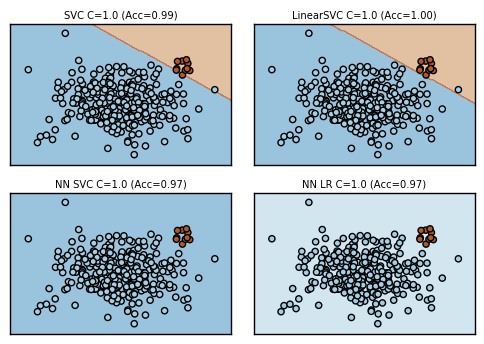
さらに偏らせてみましょう。ニューラルネットベースのものはこの状態ではうまく学習できていません。
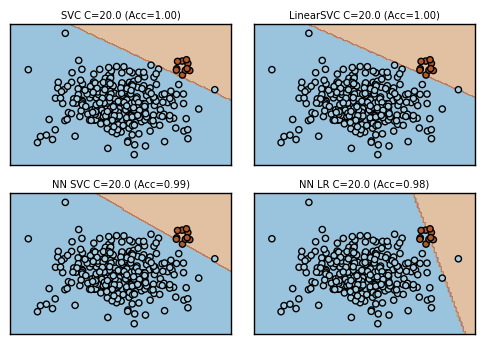
Cの値を上げ、過学習気味でやってみました。過学習させればうまくいくようです。
ただし、いくつかシードを変えつつ見てみましたが、SVC, LinearSVCはだいたいどんな$C$でもうまく行くのに対して、ニューラルネットワークはうまくいったりうまくいかなかったりです。上記だとヒンジ損失のほうがsoftmax cross entropyよりデータの偏りに強そうにも見えますが、シードによっては必ずしもそうでもないなど、どっちもどっちでした。
実データ
最後に実際のデータとしてIrisデータセットで、2つのパラメータだけ使って3クラス分類を行ってみました。このくらいのデータだとどの学習機もそれなりにうまくやれています。
考察
今回の実験結果からは、SVMは自身の経験と同様に、大体どのようなパラメータでも良好な結果を返すようでした。パーセプトロンも偏った結果意外だと、それなりの結果を返します。
これだけみると、SVMのほうが優秀な学習機に見えます。しかし、今回の実験はパーセプトロンにフェアな実験とはいえません。具体的には:
- そもそもパーセプトロンは今回のような問題には向いていない。パーセプトロンが得意とするのは、もっと複雑な問題を、多数重ねあわせたパーセプトロンで、多数のデータを元に学習することである。
- 今回の実験で用いたパーセプトロンは本来ならば多数チューニングできるパラメータがあったものを、決め打ちでやってしまった。
ただし、逆にいえば、簡単な問題を、少量のデータから、さっとチューニングなどしないで解きたいという場合は、SVMは深層学習よりも強力だといえるかもしれません。
Changes
- tl;drがSVMとNNの優劣を比べているように読めるので、主眼が比較であることを強調。