この記事はAI等の性能評価を行う方法「ROC-AUC」について記載したものです。AIの性能評価には様々なものがあります。その中でなぜ私がこのROC-AUCを選んだかですが、第一には、私が実際の業務で多用しているからであり、一見わかりづらいものではありますが、これを理解することは、数学的にも工学的にも深い示唆が得られるものだと思うからです。ある大学で講義をする機会があり、講義内容で是非触れてみたいと考えました。このROC-AUCという指標は魅力的でありながら、限界もあると言われています。多数の人が詳細を理解するのに難航しており、Web上で検索しても山ほど記事が出てきます。その中のいくつかは、正しくない記載もあると思われるので、あらためて自分で整理してここに記事にしてみたいと思います。
ここではAIとは2値分類をするものを示します。例えば、マーケティングで活用する場合、提案候補先の企業属性として、その企業の規模や、業界分類等を入力としてあたえ、受注期待度をスコアとして出力するものを示します。これはAIの性能評価だけでなく、医療統計等、例えば、PCR検査のような検査手法の開発でも使われます。
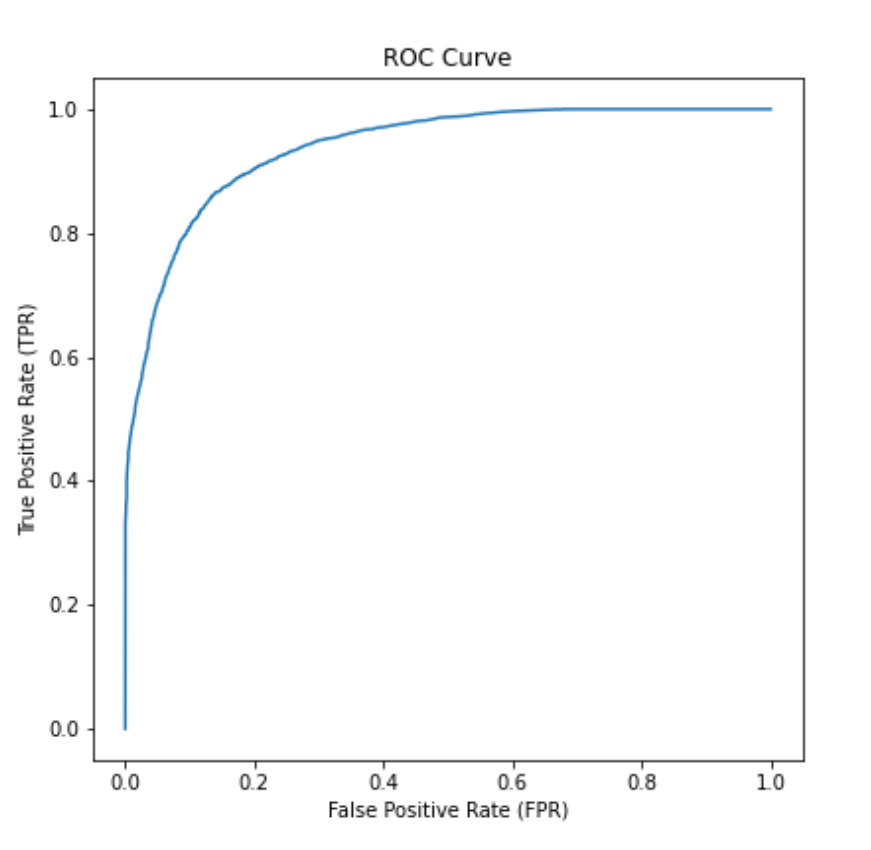
図1は、実際のROC曲線です。この曲線が左上隅の領域近くを経由するほど、つまり、曲線が左上隅に向かって膨らんでいるほど評価対象となるAIの性能は高いものとなります。
なぜ、この曲線がわかりづらいかといえば、後ほどその曲線の描き方含めて説明しますが、まずは、比較的わかりやすい別の曲線の説明からはじめたいと思います。
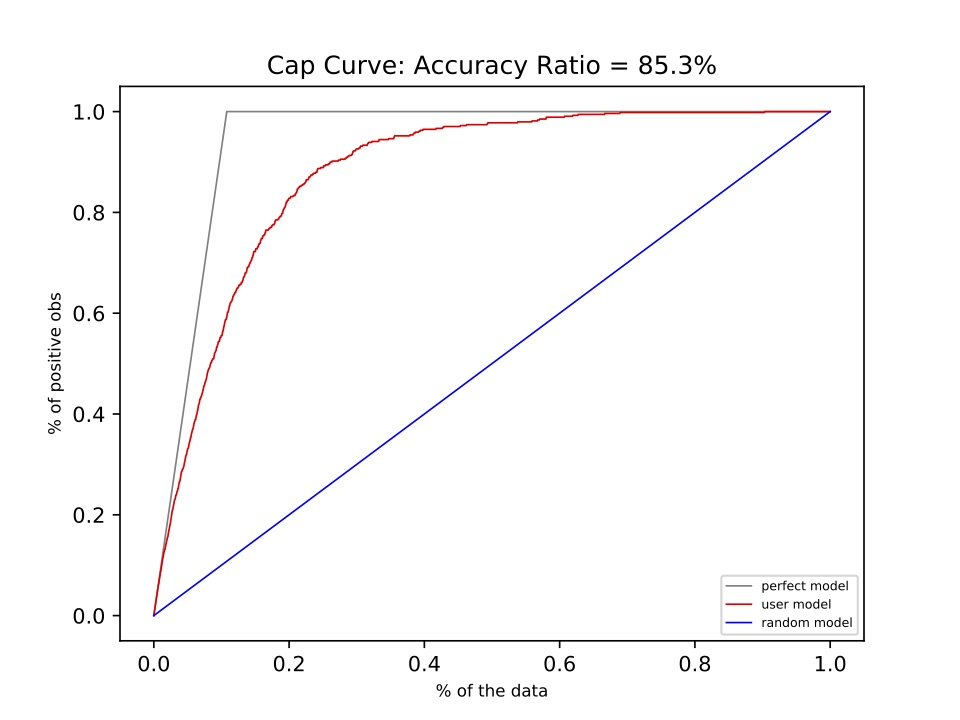
そのわかりやすい別の曲線とは、「CAP曲線」と言います。それを図2に示します。一見、ROC曲線と似ています。ROC曲線を少し右側に傾けたような形ですね。この2つの曲線の大きな違いは、CAP曲線は関数のグラフ、すなわち、X軸の値が決まると、Y軸上の値が一つだけ決まるものになります。方程式のグラフといえば、当たり前のようにこの性質を持っていますが、ROC曲線ではこの性質を持っていません。
まず、このCAP曲線の意味についてですが、CAPとはCumulative Accuracy Profiles(累積精度輪郭)の略で、 X軸はAIの出力としてのスコアの高い順にならべたとき、出力全体の数に対する上位の割合x(0.0~1.0)までを「Positiveであると予測」した場合に、合計でどれぐらいの割合を「実際のPositve」を見つけられたかを示しています。ここでAIは、いくつかの入力(「説明変数」と言います)を与えられて、何等かの出力(「目的変数」と言います)を出しますが、その入力と出力の組を多数用意して、それを学習し、その結果どれほど正しい予測ができるようになったかを答え合わせによって確認します。CAP曲線はその答え合わせの精度の確認に使うことができます。今回は、学習用のデータとして、出力は、PositiveもしくはNegativeの値を持つものとします。例えば、入力としてセールス先のお客様の属性(売り上げ、業種、所在地等)を与え、出力としては販売提案して受注すればPositive、失注すればNegativeであるとしています。AIの学習とは、この入力と出力の間の関係を再現できるようにすることであり、これをモデル化と呼びます。AIによって再現された出力は0.0~1.0のようなスコアとして提示されます。これは、「Positiveらしさ」を示すものであり、例えば0.5を閾値として、それ以上をPositive、それ未満をNegativeとして出力します。ただし、マーケティングでは限られた提案稼働の中で最大の効果を出すようにこの閾値を決めることになります。
さて、もしもこのモデルが完璧に実際のPoistiveと実際のNegativeを識別できるとしたら、実際のPositiveに対する予測スコアは全て高くなり、実際のNegativeに対する予測スコアは全て低くなります。実際のPositiveの予測スコアは、実際のNegativeよりも低いスコアよりも低くなることはありません。その場合、スコアの高い予測を上から順にカウントした時には、実際のPositiveがすべて見つかるまで、CAP曲線のグラフは、右上がりの直線上に重なることになります。すべて実際のPositiveが数え上げられたあとは、その後は高さ1.0の右方向の直線となります。
以上が完璧なモデルの場合ですが、実際は完璧なモデルをつくることは難しく、できるだけ完璧を目指すということになります。高いスコアの順に抽出していっても、途中で実際のNegativeが混ざってくる場合がありますので、上記の完璧なグラフの下側にグラフが描かれることになります。こうして、完璧なグラフにどれだけ近づけるかでモデルの良し悪しを測ることになりますが、完璧なモデルのグラフ自体が傾いているので、若干わかりづらいといえます。この完璧なモデルのグラフの右上がりの直線の傾きは、答え合わせのためのデータに含まれる実際のPositiveの割合よって変わってしまいます。このように、CAP曲線は傾いている上に、その傾きは答え合わせ用のデータに依存してしまうというわかりづらさを持っているといえます。
このわかりづらさを解決するためにROC曲線が考案されました。まず、上記の傾きを解消するために、CAP曲線上の完璧なグラフですべての実際のPositveが抽出された点を、グラフ上の(0,1)の点になるようにX軸とY軸を考えてみます。Y軸は、「すべての実際のPositiveのうちどれだけの割合をPositiveとして予測できたか」(True Positive Rate)でよさそうです。X軸については、完璧なグラフの場合に(0,1)の点を通ると考えたとき、実際のPositiveがすべて予測された場合でもゼロの値を取り得るものがよさそうです。それは「実際のNegativeのうちのどれだけの割合で、誤ってPositiveと予測したか」(False Positive Rate)を採用するべきです。
こうして、出来上がったグラフは答え合わせ用のデータの実際のPositiveの数や実際のNegativeの数の比率に依存しないものになりました。しかし、その代償として、CAP曲線ではX軸の値に対して一つだけのyの値が定まりましたが、ROC曲線では、上位からn個の予測を抽出した際に、FPRがゼロの値を持ち、異なるTPRを持つものが複数存在することになります。この性質があるので、ROC曲線は関数グラフではなく、プロット図となっていると理解することが必要です。
以上で、ROC曲線が考案された過程を辿ることができました。ROC曲線はReceiver Operation Charactristic(受信者操作特性)の略で、レーダの中で信号をどれだけ正しく補足できるかをh示す指標として考案されたものです。軍事技術の産物だったわけです。
ROC曲線を直観的に理解する
さて、こうしてROC曲線を使えば良いことはわかりましたが、グラフの形状が答え合わせデータによらないことになりましたが、その代わりX軸がFalse Positive Rate、Y軸が True Positive Rateというように直観的に理解しづらいものになってしまいました。ここをいかに理解しやすくするかについて、独自の表現方法を示したいと思います。
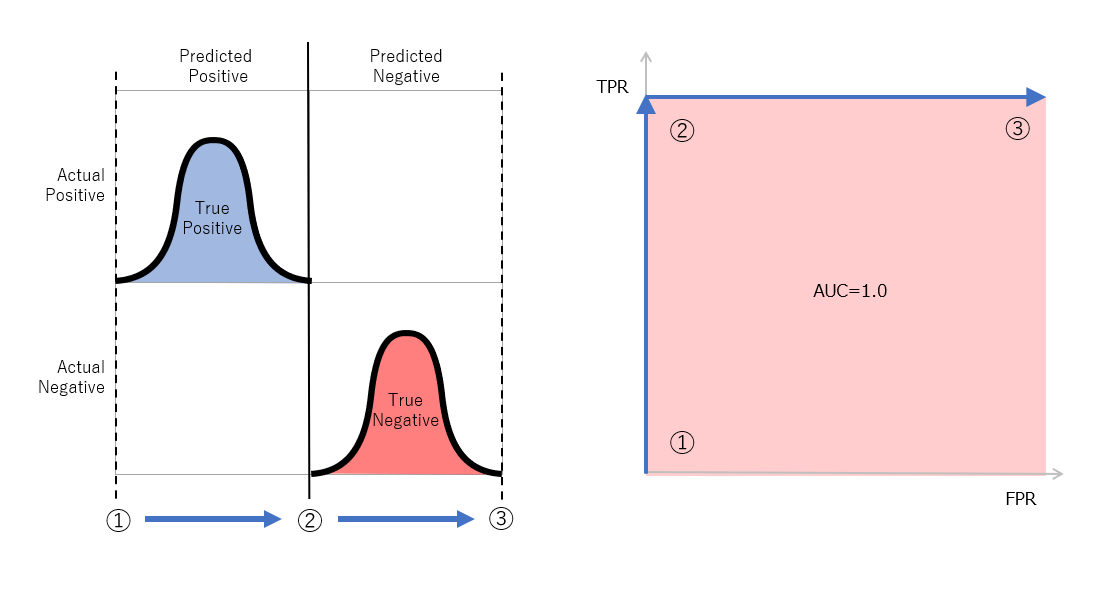
図3は、2X2の行列のうち二つの行において上下に実際のPositiveと実際のNegativeの数を棒グラフでしめしたものです。ここで横軸は左が高いスコア、右方向が低いスコアであるとします。横軸がスコアの値に対して反対方向になっているのでわかりづらいように思えるかもしれませんが、これは直観的な理解を進めるために、この2x2の行列は混同行列の配置に合わせており、左方向が「予測のPositve」、右側が「予測のNegative」となるようにしたためです。上下に配置された「実際のPositive」の分布と、「実際のNegative」の分布は実際には、答え合わせデータの中で混在していますが、あえて分けてグラフ化しています。横方向で「予測のPositive」と「予測のNegative」を区別するものはスコアの閾値となります。この閾値を左側の高いスコアから右側の低いスコアに向けて変化させながらFPRとTPRをプロットしていきます。
では実際にプロットする例を示したいと思います。図3に示したのは完璧なモデルであり、高いスコアに「実際のPositive」、低いスコアに「実際のNegative」が分布しており、それらには分布上の重なりがありません。図3上の点①から順に点②、そして点③と閾値を変化させると、それぞれ、点①ではFPR=0、TPR=0、点2ではFPR=0、TPR=1、点3ではFPR=1、TPR=1となり、これをROC曲線上に示すと図3(右)のようになります。
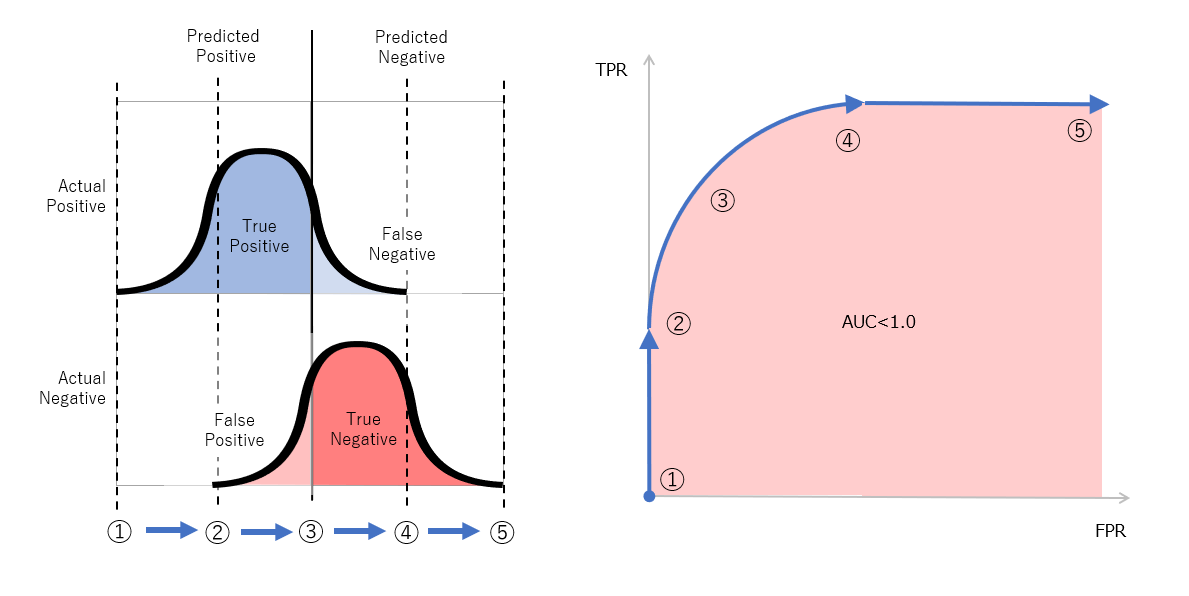
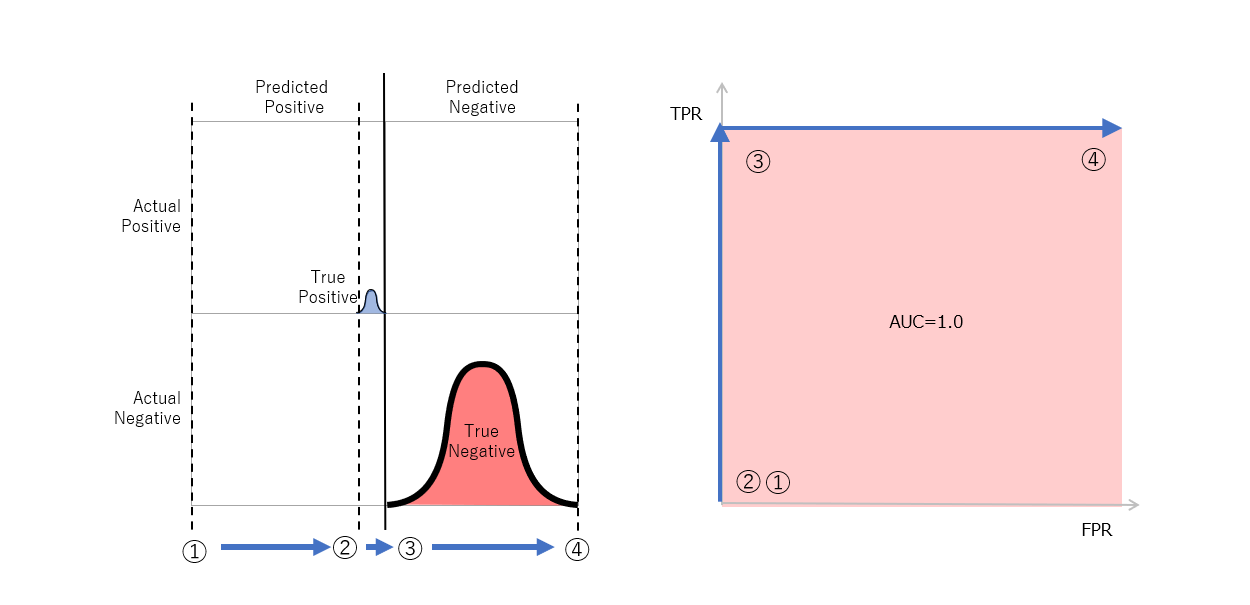
図4 完璧ではないモデルにおける分布(左)とROC曲線(右)
続いて、完璧ではないモデルの場合を図4に示します。図3(左)と比較して、実際のPositiveと実際のNegativeの分布が重なっている形となります。モデル化を行なうと通常はこのような重なりができます。この重なりが少ないほど、良いモデルであるということになります。図4上の点①ではFPR=0、TPR=0、点②に向けて、FPR=0のまま、TPRが上がっていきます。点②では、実際のNegativeの分布が重なり始めますので、FPRの値も増えはじめす。そして、点③を経て点④においてTPR=1に達しますがこの時点ではまだFPRは1になっていません。点⑤までいくとFPR=1、TPR=1となります。
以上のような図示方法によりROC曲線のプロット方法を直観的に理解しやすくなるのではないでしょうか。
ROC-AUCの算出
ROC曲線では、モデルの精度を示すために、まず完璧なモデルの指標値を1として、それにどれだけ近づけているかを数値化しするその手法を使っています。この手法はROC-AUCと言います。AUCはArea Under Curve(曲線下面積)の略であり、ROC曲線のグラフにおいては、完璧なモデルの場合に最大値1.0、ランダムなモデルの場合に0.5の値を取ります。このように、理想的なグラフとの違いを面積の比率で表現する手法は応用範囲も広そうです。
ROC-AUCの欠点
以上のように、ROC-AUCがモデルの評価指標としては優れている一方で、問題もあります。それは、答え合わせデータにおける実際のPositveと実際のNegativeの個数に偏りがある場合に起きることがあります。
ROC曲線のグラフでX軸、Y軸として使っているTPRもFPRもそれぞれ、実際のPositiveと実際のNegativeに対する比率(Rate)であり、両者は独立しており、「実際のNegativeが多すぎるのでTPRが高くなる」といったことは起きないように思われます。不均衡なデータではROC-AUCが不適切だという根拠はどこからきているのでしょうか。
実際のPositve数に対して、実際のNegative数が大きくなるとどのような影響があるのかを示します。図5のように予測スコアで並べたときに、実際のPositiveと実際のNegativeがしっかり分かれているときはAUCが1.0になることは図3の説明の際に示しました。ここが、重なりを持っていた場合にどうなるでしょうか。
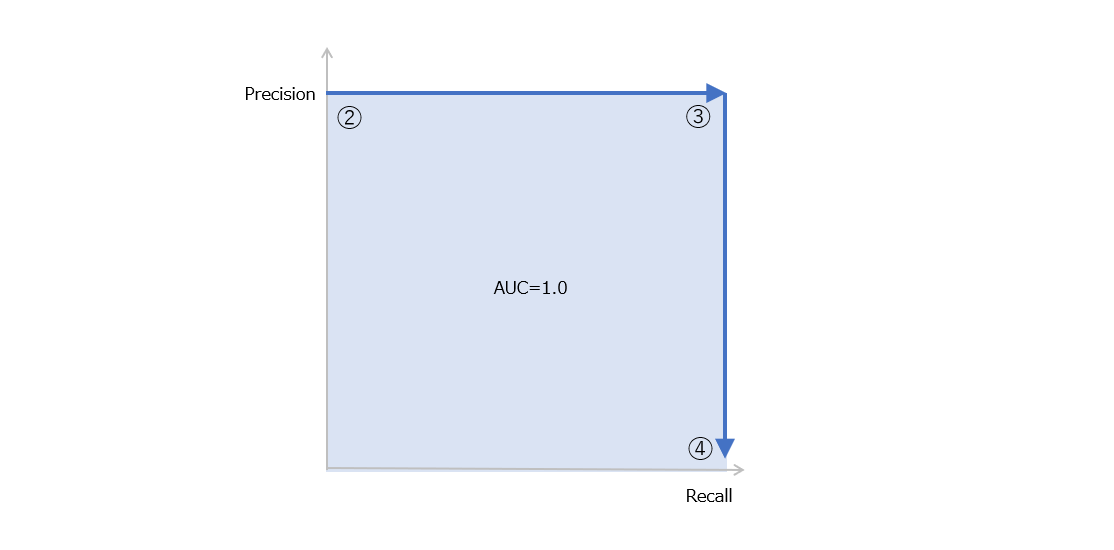
図5 実際のPositveを高いスコア、実際のNegativeを低いスコアに区別できているモデルの例。実際のNegativeが多くても問題ない。下の図はこの場合のPR曲線。
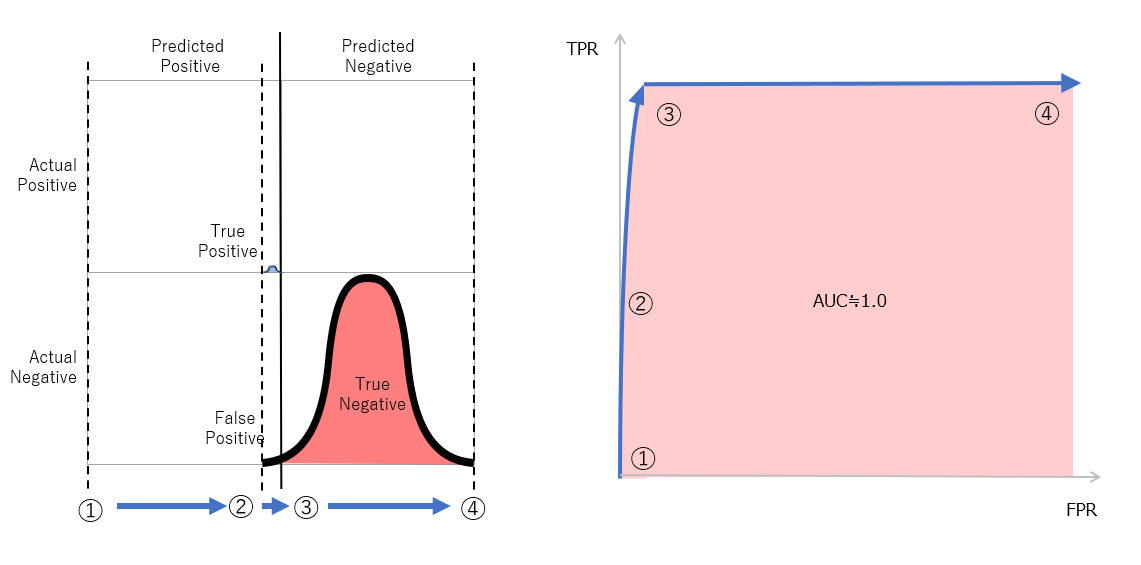
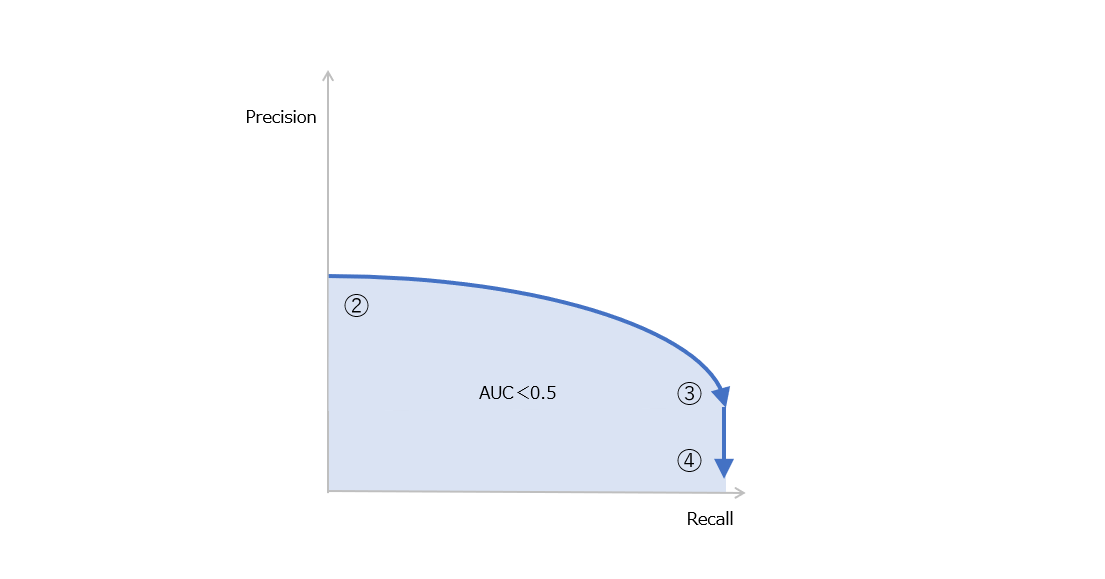
図6 実際のNegativeが多い状態で重なっている例。下の図はこの場合のPR曲線。
図6では、実際のPositiveが少ないので重なりは小さいものの、重なっている部分では実際のPositiveと実際のNegativeが混在しているので、望ましいモデルではないものの、重なっていない部分で大量の実際のNegativeがあるので、TPRが高くなってもFPRは小さいままであり、AUCは高い値となります。これが、ROC-AUCが適切とならない最たる例となります。一方で、別の場合として図9を見てください。
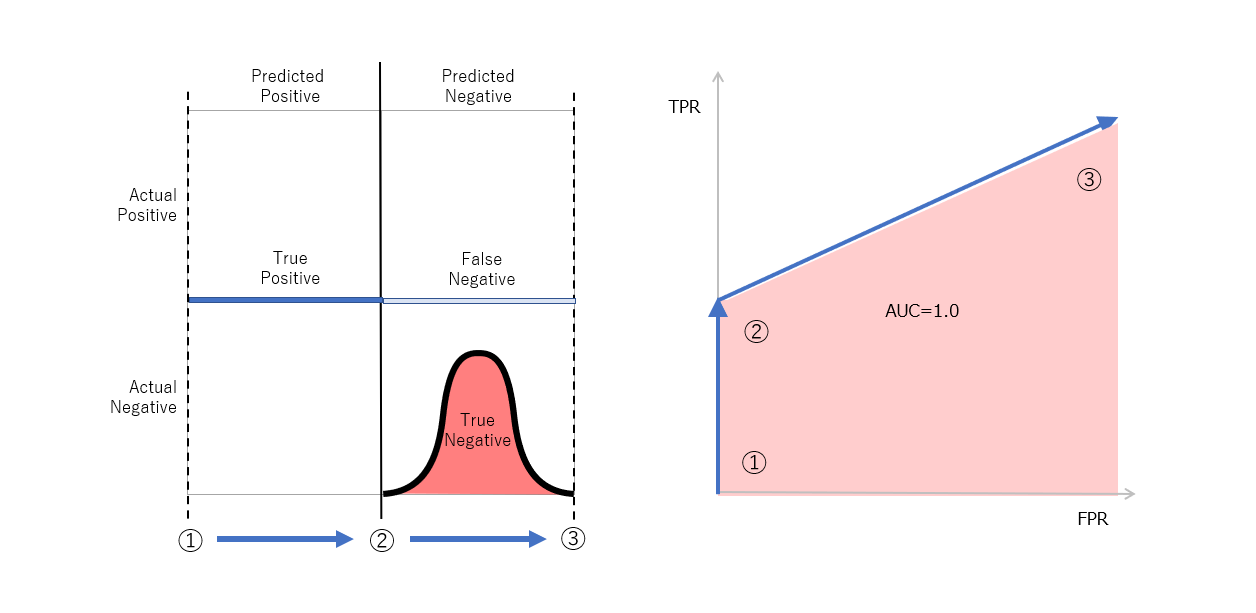
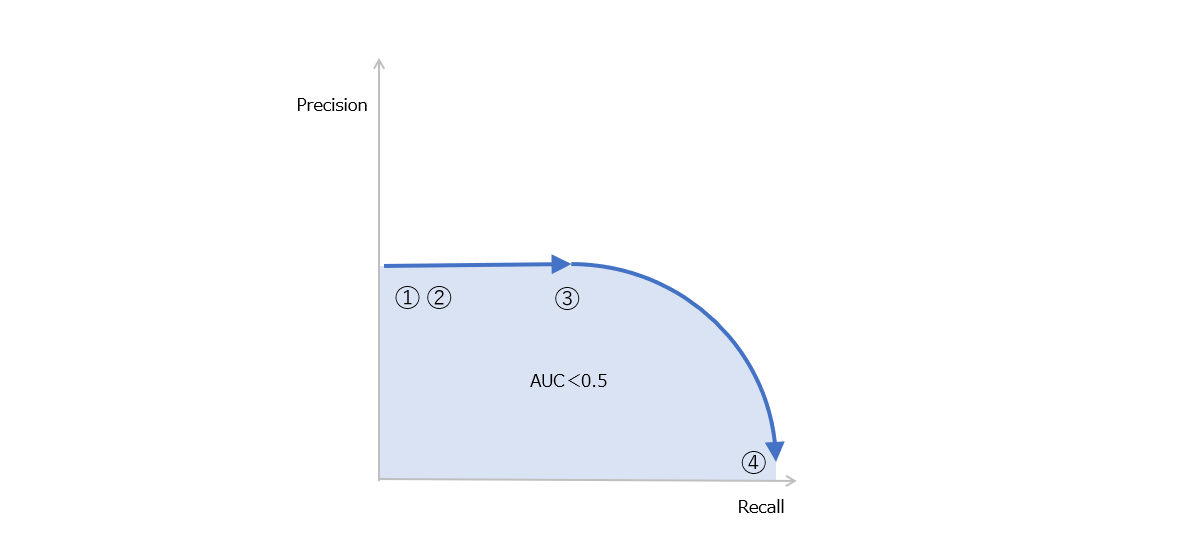
図7 実際のNegativeは低いスコアとなり、実際のPositiveは広いスコア範囲に分布する例
別の例として図7に示したものは、実際のNegativeに対してのみ低いスコアを出して正しい予測をするものの、実際のPositiveに対しては正しい予測ができない例です。この様な場合も、閾値を1.0から順に下げていく際に、実際のNegativeに対してPositveであると予測しはじめるまでは、FPRは0のままTPRだけが上がるので、図10(右)に示すようなROC曲線となります。これは、途中まではしっかりとPositive判定ができているのでAUCがそれなりに高くなることは不適切ではありません。(他の記事では、これを不適切な例として記載していますが、納得しかねます。)
以上の様に、実際のPositveの個数と実際のNegativeの個数の不均衡さだけではROC-AUCが必ずしも不適切になることは言えません。これは、実際のPositveと実際のNegativeの分布を確認した上で、実際のPositive部分だけに着目して予測モデルの性能を評価するべきであるかどうかを考える方が良いでしょう。
では、ROC-AUCで予測モデルの精度を比較することが不適切な時にどうすればいいのでしょうか。この時には、PR-AUCの採用を検討します。これはPR曲線(Prescision-Recall曲線)のAUCです。PR曲線とは、X軸にRecall(これはTrue Positive Rateと同じであり、ROC曲線ではY軸として採用していたもの)、Y軸をPrecision(ある閾値以上の予測スコアをPositiveとしたときに、予測したPositive全体の中で実際のPositiveが含まれている比率)とした時に、閾値を変化させた時のこれらの値をプロットしたものです。
PR曲線は、横軸がRecall(True Positive Rate)となっており、実際のPositiveが分布するスコアの範囲のみがPR-AUCの算出に考慮されます。これは、ROC曲線の横軸がFalse Positive Rateとなっており、実際のNegativeが分布するスコアの範囲のみが考慮されることと対照的です。故障予測等、実際のPositiveが実際のNegativeに対してかなり少ない場合には、実際のPositiveの分布が実際のNegativeの分布に対して少ししか重なっていないことが起きえます。この時、ROC-AUCには実際のPositiveの分布に関わる部分の性能を十分に表現できません。
もしもその予測モデルが実際のPositiveを高スコア、実際のNegativeを低スコアとして完璧に区別できる場合は、Recallが0.0から1.0となった時、すなわち、上位スコアから順に閾値を下げていった時、閾値以上のスコアに含まれている実際のPositiveの数は次第に増え、すべての実際のPositiveを包含するような閾値にたどり着くまでの間、Precisionが1.0のままとなります。すなわち、その閾値以上の予測スコアを持つのは実際のPositiveだけとなります。この場合、PR-AUCは1.0となります。実際は、閾値以上に実際のNegativeが入ってくることになり、それにしたがってPrecisionの値は減少するので、PR-AUCも下がることになります。
ROC-AUCとPR-AUCの使い分け
PR-AUCがROC-AUCとどう違うかについてですが、PR曲線はX軸がRecallとなっていることから、閾値を変化させる際に、実際のPositiveをすべてPositiveと予測した時点でAUCが決まってしまうことに対して、ROC曲線ではX軸がFPRとなっていることから、実際のNegativeをPositiveであると予測し始める時点から、実際のNegativeをすべてPositveと判定してしまう時点までがAUCを計算する対象となります。つまり、AUC算出の範囲がPR-AUCでは実際のPositiveが存在する範囲だけを対象とするのに対して、ROC-AUCは実際のNegativeが存在する範囲だけが対象となります。予測スコアにおいて実際のPositiveが取りうる範囲が小さく、特にその部分に着目すべき問題設定がなされている場合は、その部分を判定するのはPR-AUCですので、PR-AUCを活用することが良いでしょう。
実際のPositiveが取りうる範囲が小さいときでも有効な指標として使うことのできるPR-AUCが万能であるのかといえば、PR-AUCにも欠点があります。例えば、完全にランダムな予測しかしないモデルであるとき、PR-AUCは、答え合わせ用データに占める実際のPositiveの比率に等しくなります。一方で、ROC-AUCはランダムな予測を行なうモデルでは、答え合わせ用データの分布によらず、その値は0.5となります。従って、モデル間の比較を行なう時、この違いを念頭に置く必要があります。
基本的にはモデル間での比較をROC-AUCを使って行い、不均衡データの場合はPR-AUCを併用することがよいでしょう。
まとめ
本記事では、ROC-AUCの理解を進めるために、その前段としてのCAP曲線について解説し、さらには、答え合わせ用データの分布を表現するために、混同行列の形式を参考にした表記方法を紹介しました。ROC-AUCはその限界として、答え合わせ用データが不均衡担っている場合かつ実際のPositiveの分布が予測スコアに対して狭い範囲になっている場合に十分な判別能力を持ちません。その解決案としてのPR-AUCを紹介しましたが、PR-AUCにもランダムな予測との比較がその値だけではできないという欠点があるため、両者の併用をするべきであるということを示しました。