アドベンドカレンダー用に、今年出会った素敵なアルゴリズム「いもす法」の解説を書いてみます。
イメージしやすいように、できるだけ図表をいれて解説してみます。
いもす法とは
加算を効率的に行うアルゴリズムです。連続した領域で多次元にも適用できるそうです。
今回は、よく見る1次元、2次元だけでなく、3次元に挑戦してみます。
1次元いもす法
startとendがわかっている以下のような例題で使用できます。
例題
ある塾の自習室は一日一回何時間でも連続して利用することができます。
自習室に1時限目から10時限目まで開放されています。
入退室は毎時0分のタイミングでしかできません。
塾生の利用開始時限と終了時限が与えられる時に、最も利用人数が多かった時の人数を求めなさい。
入力データは下記のように与えられます。
絵にすると下記のようになり、最も利用人数が多い時の人数は4人とすぐにわかります。
よって、こんな配列を作成することを目的とします。
result = [1, 3, 3, 3, 4, 3, 3, 3, 2, 1];
ナイーブな解法
ナイーブに解くと、要素数10の配列を0で初期化し
result = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
各人のデータごとに利用時限に該当する要素をインクリメントすればよいです。
//Aさん 2 8
result = [0, 1, 1, 1, 1, 1, 1, 1, 0, 0];
//Bさん 1 10
result = [1, 2, 2, 2, 2, 2, 2, 2, 1, 1];
//Cさん 2 5
result = [1, 3, 3, 3, 3, 2, 2, 2, 1, 1];
//Dさん 5 9
result = [1, 3, 3, 3, 4, 3, 3, 3, 2, 1];
目的の配列が完成したので、配列の要素から、maxをとれば求められます。
いもす法
同様に配列を作成します。
result = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
各人のデータごとに開始時限に1、終了時限の次に-1をいれます。
Bさんのように最後までいる人用に、配列数を1つ増やすか、最期の-1は処理しないようにします。
どちらにするかは問題によりますが、if文を入れない方がバグが減りそうなので、今回は配列数を1つ増やしてます。
//要素数を11
result = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
//Aさん 2 8
// 2番目を+1、9番目を-1
result = [0, 1, 0, 0, 0, 0, 0, 0, -1, 0, 0];
//Bさん 1 10
// 1番目を+1、11番目を-1
result = [1, 1, 0, 0, 0, 0, 0, 0, -1, 0, -1];
//Cさん 2 5
// 2番目を+1、6番目を-1
result = [1, 2, 0, 0, 0, -1, 0, 0, -1, 0, -1];
//Dさん 5 9
// 5番目を+1、10番目を-1
result = [1, 2, 0, 0, 1, -1, 0, 0, 0, -1, -1];
ここで察しのいい人はこの配列から
result = [1, 3, 3, 3, 4, 3, 3, 3, 3, 2, 1];
が生成できることに気づくかもしれません。頭の体操。。。ポクポクポク
各配列要素は、各配列要素までの和(累積和)で求められます。
result[1] = result[0] + result[1]
result[2] = result[1] + result[2]
(略)
ループで書くと
for( int i = 1; i < result.length; i++){
result[i] = result[i-1] + result[i];
}
入口で人が入ったら、1加算し、帰ったら、1減算すると捉えられると、1次元のいもす法は理解しやすいと思います。
2次元いもす法
平面に四角形を座標軸と平行に、ランダムに重ねて配置した状態から何らかを求めます。
最も重なっている枚数、四角形が置かれている面積、置かれていないところの面積とか。
例題
任意の大きさの四角形をxy座標系に並べます。
頂点の座標は正の整数で、左上(lx, ly)、右下(rx, ry)の座標が与えられます。
複数の四角形を並べた時の面積の合計を求めよ。
(2次元いもす法のための問題ですね。。)
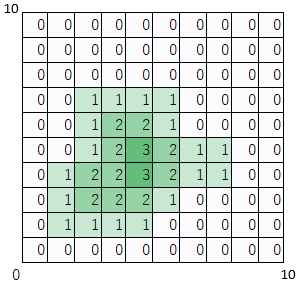
図に書くと状況はわかりやすくなります。
面積を求めるには、色がついたマスを数えればよいです。
よくある解説では、左上が(0, 0)、右下が(10, 10)になっていますが、数学脳なため上下反転させてます。
面積だけだと以下のような配列を表現すればよいことになります。
(図をEXCELで作成しているので面積は領域選択するだけ求められるという。。。)
いもす法を使用すると重なりを考慮した以下の2次元配列が求められます。
ナイーブな解法は、座標に注意してひたすら二重に回せばいいので省略します。
いもす法では各四角形の左下と右上の外側+1、左上と右下の外側に-1を入れます。
まずは四角形Aについてだけ入れた状態。
右上に1を入れるのが直観的には、僕には感じれない。。

1次元の時と同じように、右方向と上方向に累積話をとります。まず右方向。
ー1があるとその先が0のままになります。

そして上方向。
1が横に並んで上に攻めあがってきますが、-1で消失します。

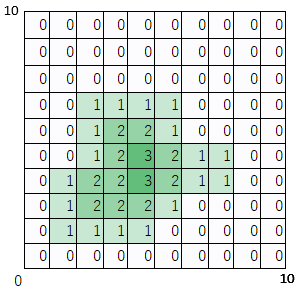
期待していた形になりました。まず1枚の四角形の分だけで解説しましたが、問題を解く際はすべての四角形の1と-1を一旦入れてから、累積話をとります。この手順を遡っていくと、右上に1を置いておく理由が何となくわかります。
1次元の時と同じように、右方向と上方向に累積話をとります。まず右方向。

そして上方向。
図解で解説しましたが、コードではxy[10][10]で同じ計算を行うだけです。
for( int i = 0; i < 10; i++){
for( int j = 1; j < 10; j++){
xy[i][j] = xy[i][j-1]+xy[i][j]
}
}
for( int i = 1; i < 10; i++){
for( int j = 0; j < 10; j++){
xy[i][j] = xy[i-1][j]+xy[i][j]
}
}
3次元いもす法
次は3次元で考えてみました。
どの座標も異なる2つの頂点を含み、各辺は、座標軸と並行な直方体の体積で考えました。
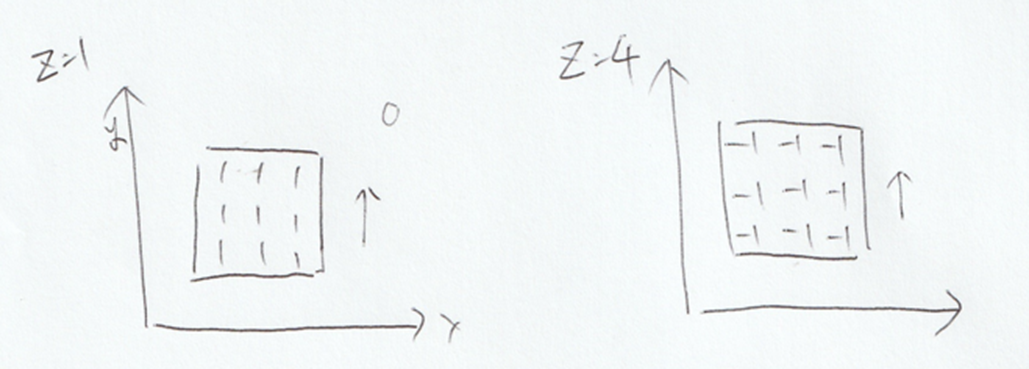
頂点が、(1, 1, 1)と(4, 4, 4)を通り、3×3×3=27の下図左のような直方体で考えます。
1が入った箱が27個ある状態を想像してください。
1とー1をいい感じに配置して、累積和を取っていけば求められることを期待したいところです。
初めは1次元増えたことにより、(4,4,4)の斜め上あたりに、-2か-3でもくるのかなと考えました。
ただ、適当に配置して計算しても、どうも辻褄が合わないので、逆算していきました。
1で埋め尽くされた状態にするには、いもす法の考え方だと、1で埋め尽くされた面と-1で埋め尽くされた下図右の状態が必要になります。

ここからはまさかの手書きです。
2段目は1が並んでいるので、2次元の時と同じ状態です。5段目の-1も2次元のをひっくり返せばいいことは、直観的にわかります。
よって、下図のように、並べれば良さそうですが、わかりにくくなったので、xy平面と平行に面を切断して記載します。
(立体で表現するのをあきらめます)

xy平面に並行に切断するとこんな感じです。
一応、検算しておきます。
x軸方向に累積和を取った状態。数字がはいってないところは、0です。
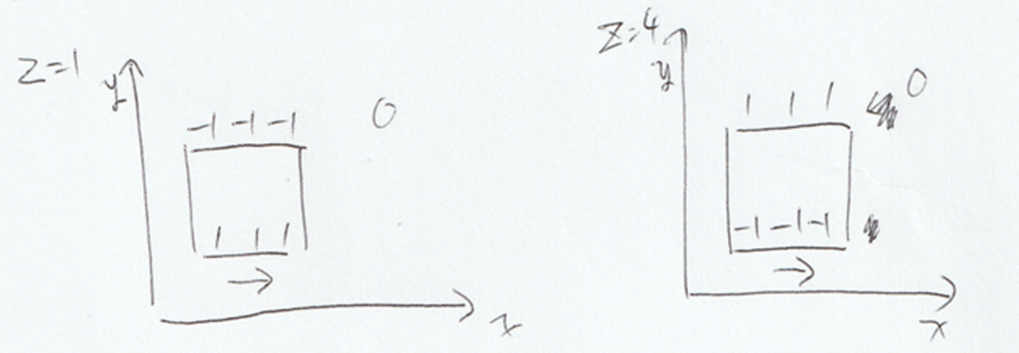
そこから、y軸方向に累積和をとると期待していた形になりました。
そこから、z軸方向に累積和をとると期待していた形になりました。
3次元のいもす法を使って、直方体が重なっている部分の体積を求める問題を解きました。
1と-1を置いて、和を取っていくだけの単純なコードです。
https://github.com/konakagawa/Imos3
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String line = sc.nextLine();
int N = Integer.parseInt(line);
// cube index
// 0:min 頂点、1:max 頂点
// x,y,z
int[][][] cubes = new int[N][2][3];
for (int i = 0; i < N; i++) {
line = sc.nextLine();
String[] str = line.split(" ");
for (int j = 0; j < 3; j++) {
cubes[i][0][j] = Integer.parseInt(str[j]);
cubes[i][1][j] = Integer.parseInt(str[j + 3]);
}
}
// 領域の初期化 area[z][y][x]
int[][][] area = new int[10][10][10];
for (int i = 0; i < area.length; i++) {
for (int j = 0; j < area[i].length; j++) {
Arrays.fill(area[i][j], 0);
}
}
// 1と-1をコーナーに設置
for (int i = 0; i < N; i++) {
int[] xyz = cubes[i][0];
int[] XYZ = cubes[i][1];
// 下の面
area[xyz[2]][xyz[1]][xyz[0]] += 1;
area[xyz[2]][XYZ[1]][xyz[0]] += -1;
area[xyz[2]][xyz[1]][XYZ[0]] += -1;
area[xyz[2]][XYZ[1]][XYZ[0]] += 1;
// 上の面
area[XYZ[2]][xyz[1]][xyz[0]] += -1;
area[XYZ[2]][XYZ[1]][xyz[0]] += 1;
area[XYZ[2]][xyz[1]][XYZ[0]] += 1;
area[XYZ[2]][XYZ[1]][XYZ[0]] += -1;
}
// 領域の計算
// x軸方向に累積和
for (int i = 0; i < area.length; i++) {
for (int j = 0; j < area[i].length; j++) {
for (int k = 1; k < area[i][j].length; k++) {
area[i][j][k] += area[i][j][k - 1];
}
}
}
// y軸方向に累積和
for (int i = 0; i < area.length; i++) {
for (int j = 1; j < area[i].length; j++) {
for (int k = 0; k < area[i][j].length; k++) {
area[i][j][k] += area[i][j - 1][k];
}
}
}
// z軸方向に累積和
for (int i = 1; i < area.length; i++) {
for (int j = 0; j < area[i].length; j++) {
for (int k = 0; k < area[i][j].length; k++) {
area[i][j][k] += area[i - 1][j][k];
}
}
}
// 結果の出力
int taiseki = 0;
for (int i = 0; i < area.length; i++) {
for (int j = 0; j < area[i].length; j++) {
for (int k = 0; k < area[i][j].length; k++) {
// 一つ以上重なっている場合
if (area[i][j][k] > 1) {
taiseki++;
}
}
}
}
System.out.print(taiseki);
sc.close();
}
}