【100 numpy exercises】で"numpy力"を底上げ(1~10問目)
前回の記事から続きで11~20問目を解いていきます。
11. Create a 3x3 identity matrix (★☆☆)
『3×3の単位行列を作れ』
※identity matrix=単位行列
n×nの単位行列はnp.eye(n)で生成できます。
Z = np.eye(3)
print(Z)
実行結果
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
12. Create a 3x3x3 array with random values (★☆☆)
『3x3x3の配列を作れ(要素はランダム)』
乱数を生成する場合はnumpy.randomモジュールを使用します。
Z = np.random.rand(3,3,3) # 3x3x3配列の乱数(0.0以上1.0未満)
print(Z)
実行結果
[[[0.44518095 0.00924118 0.59004146]
[0.12450099 0.91674964 0.77679575]
[0.28061072 0.03625354 0.87043565]]
[[0.76171958 0.39143584 0.02266029]
[0.51873782 0.60923224 0.69941338]
[0.41821728 0.65331316 0.74005185]]
[[0.25365995 0.45885229 0.41108347]
[0.74013277 0.44224959 0.39538442]
[0.27518178 0.50242514 0.54273645]]]
整数の乱数で配列を作りたい場合はnumpy.random.randint()を使用します。
numpy.random.randint(low, high, size)という形で引数を指定します。
→ low以上high未満の整数の乱数でsizeに指定したサイズで配列を生成する。
Z = np.random.randint(1,10,(3,3,3)) # 3x3x3配列の乱数(1以上10未満の整数)
print(Z)
実行結果
[[[4 2 8]
[2 5 9]
[9 4 6]]
[[6 1 8]
[1 6 9]
[5 3 5]]
[[8 9 8]
[8 9 4]
[7 8 4]]]
13. Create a 10x10 array with random values and find the minimum and maximum values (★☆☆)
『10x10配列を乱数で生成して、要素の最小値と最大値を見つけろ』
前半の乱数生成は前問の復習ですね。問題は後半です。
arrayの最小、最大はmin()、max()という関数で表示することができます。わかりやすいですね。
Z = np.random.rand(10,10)
print(Z)
print(Z.min())
print(Z.max())
実行結果
[[0.52234883 0.04961266 0.26979588 0.35807264 0.58767559 0.66650289
0.51751858 0.00749977 0.64916673 0.52928179]
[0.84590062 0.475141 0.98199741 0.85117845 0.07182633 0.85569791
0.68031337 0.39577058 0.3102539 0.05988267]
[0.1908481 0.44464734 0.42211624 0.33883119 0.47234289 0.88443684
0.67840264 0.11499548 0.01561011 0.62472268]
[0.68165249 0.56003177 0.69289739 0.01834723 0.82186756 0.33528515
0.33715765 0.89662065 0.91279419 0.95973881]
[0.16768925 0.88251896 0.7545505 0.80567805 0.0875194 0.86998789
0.42720398 0.73700043 0.95089544 0.87874673]
[0.61277308 0.20511706 0.7039127 0.55107676 0.00495881 0.93791274
0.5540698 0.17465328 0.17021889 0.75724567]
[0.20103278 0.0402996 0.86112665 0.22460515 0.49205103 0.67606385
0.97352361 0.48226577 0.1698369 0.75163188]
[0.08707084 0.94483062 0.82773455 0.849915 0.54699492 0.63773099
0.88614943 0.839312 0.2898842 0.49742767]
[0.50516571 0.25980059 0.78911141 0.17191684 0.41938205 0.98415545
0.22282797 0.06791284 0.44208603 0.30956802]
[0.49319972 0.09882225 0.08468636 0.64297834 0.57264345 0.49475321
0.0089241 0.28765751 0.84352742 0.962471 ]]
0.004958805565047131
0.9841554497271033
14. Create a random vector of size 30 and find the mean value (★☆☆)
『サイズが30のベクトルを作り、平均値を求めよ』
arrayの平均値を求めるにはmean()を使います。これもまたそのままですね。
Z = np.random.rand(30)
print(Z)
print(Z.mean())
実行結果
[0.71731749 0.27092985 0.47882913 0.94756227 0.35222887 0.45151348
0.83705811 0.66280134 0.43406269 0.53061543 0.88052437 0.93703825
0.02288098 0.4235356 0.69145184 0.97566151 0.60787705 0.15327448
0.85466264 0.8320094 0.31804771 0.43561608 0.8271854 0.57419325
0.83537801 0.33995759 0.92256564 0.40740555 0.70334292 0.13671002]
0.5854078986104199
15. Create a 2d array with 1 on the border and 0 inside (★☆☆)
『境界が1で内部が0の二次元配列を作れ』
いくつかやり方があるとは思いますが、一旦すべて"1"の配列を作ってから、内部を"0"に書き換えるのが簡単そうです。
内部を"0"で書き換えるにはスライスを使って範囲指定をします。
10×10の配列で作ってみましょう。
Z = np.ones((10,10))
Z[1:-1,1:-1]=0
print(Z)
実行結果
array([[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]])
16. How to add a border (filled with 0's) around an existing array? (★☆☆)
『既存の配列の周りに0の要素を追加するには?』
これは少し悩みますね。
hintを見てみます。
hint: np.pad
np.pad()という関数を使えば良さそうです。
このpadはpadding(埋める)ということです。
ある配列の周りに別の要素を埋めることができる関数です。
例えば、a = [1,2,3]という一次元配列があったとしましょう。
この配列の前後1つを0で埋めたい場合は、
print(np.pad(a, [1,1], mode="constant"))
とします。
実行結果
[0, 1, 2, 3, 0]
numpy.pad(array, pad_width, mode=xxx)
array:既存の配列
pad_width:arrayの前後いくつ分を埋めるか。(before_n, after_n)のように指定します。前後が同じ場合はnのように指定してもいいです。
mode:どの値で埋めるか。"constant"を指定すると、定数(デフォルトは0)で埋めます。0以外で埋めたい場合は、constant_values=Nのように埋めたい値Nを指定します。
2次元配列の場合はどうなるのでしょうか?
やってみましょう。
Z = np.array([[1,2,3],
[4,5,6]])
print(np.pad(Z, [1,1], mode="constant",constant_values=99))
実行結果
[[99 99 99 99 99]
[99 1 2 3 99]
[99 4 5 6 99]
[99 99 99 99 99]]
元の配列を囲むようにして"99"が埋まりましたね。
17. What is the result of the following expression? (★☆☆)
『次の結果は?』
0 * np.nan
np.nan == np.nan
np.inf > np.nan
np.nan - np.nan
np.nan in set([np.nan])
0.3 == 3 * 0.1
それぞれの行を実行した結果が問われています。
まず、頻出するnp.nanとは何者かなのですが、「nan(NaNとも書く)」とは"Not a Number"、日本語では"非数"のことです。
これは「数であって数にあらず」とでも言いましょうか、
浮動小数点演算の結果として数であることが期待されているにも関わらず、数でなかった場合を表すシンボルです。
このNaNには大きな特徴が2つあります。
1.どんな値を比較(==や大小)しても結果はFalseになる
# NaNとどんな値を比較(==や大小)しても結果はFalseになる
print(np.nan == 10)
print(np.nan > 10)
print(np.nan < 10)
print(np.nan == np.nan)
実行結果
False
False
False
False
2.どんな値を加減乗除しても結果はNaNになる
# NaNにどんな値を加減乗除しても結果はNaNになる
print(np.nan + 10)
print(np.nan - 10)
print(np.nan * 10)
print(np.nan / 10)
実行結果
nan
nan
nan
nan
ちなみにtype(np.nan)と打ってnp.nanの型を調べてみるとfloatとなっています。
まさに「数であって、数でない」。少し不思議ですね。
では、以上を踏まえて一行ずつ問題を見ていきます。
0 * np.nan
NaNに何を掛けても結果はNaNです。それは0であっても例外ではありません。
print(0 * np.nan)
実行結果
nan
np.nan == np.nan
NaNとどんな数を比較してもFalseです。
print(np.nan == np.nan)
実行結果
False
np.inf > np.nan
np.infというのは"無限大"のことです。
NaNとどんな数を比較してもFalseになります。無限大と比較してもFalseです。
print(np.inf > np.nan)
実行結果
False
np.nan - np.nan
NaNとどんな値を加減乗除してもNaNとなります。
print(np.nan - np.nan)
実行結果
nan
np.nan in set([np.nan])
np.nanという集合の中にnp.nanがあるかということですが、これはTrueになります。
print(np.nan in set([np.nan]))
実行結果
True
0.3 == 3 * 0.1
これは一見Trueになりそうなのですが、結果はFalseになります。
10進数では0.3は0.3なのですが、コンピュータ内部では浮動小数点数を2進数で表現しています。
そのため、10進数の0.3とはまったく同じ値を表現することができないのです。
実際に見たほうがわかりやすいので、「0.3」と「3 * 0.1」をformat()を使って小数点以下20桁を表示させてみましょう。
print(format(0.3, '.20f'))
print(format(3 * 0.1, '.20f'))
実行結果
0.29999999999999998890
0.30000000000000004441
確かにどちらも厳密には0.3でないことがわかりますね。
なので、「0.3」と「3 * 0.1」は等価ではないので0.3 == 3 * 0.1はFalseとなります。
print(0.3 == 3 * 0.1)
実行結果
False
18. Create a 5x5 matrix with values 1,2,3,4 just below the diagonal (★☆☆)
『対角成分のすぐ下の成分が1,2,3,4となる5x5の配列を作れ』
わかりづらいのですが、このような配列を作ればいいのでしょう。

配列の対角成分を扱うにはnp.diag()を使います。
引数にベクトルやリストを指定すると、それを対角成分とした正方行列を作成します。
print(np.diag([1,2,3,4]))
実行結果
[[1 0 0 0]
[0 2 0 0]
[0 0 3 0]
[0 0 0 4]]
np.diag()にはもう一つkというパラメータを指定することができます。
例えば、np.diag(v,k=n)とすると、対角成分のn個上の要素がvになるような配列を生成します。
(nが負の数の場合には、対角成分のn個下の要素がvになります)
今回の問題は対角成分ではなく、対角成分のすぐ下の要素を1,2,3,4としたいので、
np.diag()の引数でk=-1と指定します。
Z = np.diag([1,2,3,4],k=-1)
print(Z)
実行結果
[[0 0 0 0 0]
[1 0 0 0 0]
[0 2 0 0 0]
[0 0 3 0 0]
[0 0 0 4 0]]
19. Create a 8x8 matrix and fill it with a checkerboard pattern (★☆☆)
『8x8のcheckerboard patternの配列を作れ』
checkerboard patternというのは、こういう模様のことです。市松模様とも言いますね。
このパターンの白色を"0"、黒色を"1"として、次のような配列を作ればいいということです。
まず要素がすべて0の8x8の配列を作ってから、一つおきに要素を1に書き換えていく方針にします。
Z = np.zeros((8,8),dtype=int)
Z[::2,::2] = 1
Z[1::2,1::2] = 1
print(Z)
実行結果
[[1 0 1 0 1 0 1 0]
[0 1 0 1 0 1 0 1]
[1 0 1 0 1 0 1 0]
[0 1 0 1 0 1 0 1]
[1 0 1 0 1 0 1 0]
[0 1 0 1 0 1 0 1]
[1 0 1 0 1 0 1 0]
[0 1 0 1 0 1 0 1]]
20. Consider a (6,7,8) shape array, what is the index (x,y,z) of the 100th element?
『6×7×8の多次元配列において、100番目の要素のインデックス(x,y,z)は?』
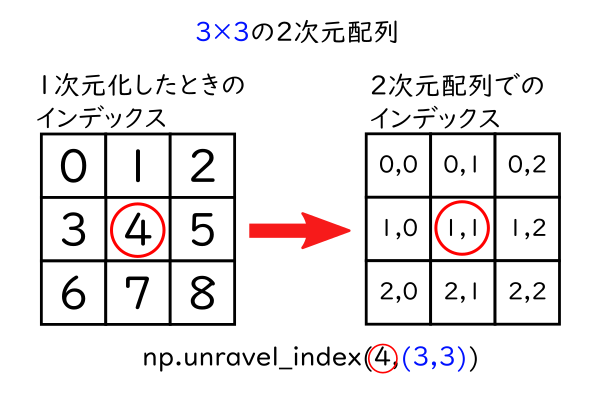
多次元の配列も1次元に並べて頭からインデックスを振っていくことができます。そのとき、例えば上の図でいうところの5番目の要素(インデックスは4)は、3×3の2次元配列のインデックスで表すと**(1,1)**と表現することができます。
np.unravel_index()というのは、一次元で表現するインデックスを多次元配列でのインデックスに変換する関数と思ってもらえればよいと思います。
np.unravel_index(indices,shape)
引数のindicesは一次元でのインデックスです。shapeは多次元配列のサイズを指定します。
今回は100番目の要素のインデックスを6×7×8の多次元配列でのインデックスで表現したいので、下記のように書くことができます。
(100番目なのでインデックスは99になります)
print(np.unravel_index(99, (6,7,8)))
実行結果
(1, 5, 3)
今回はここまでです。歯ごたえのある問題が出てきました。
次回は21~30問目を解いていきます。