はじめに
hello😇初めてのアドベントカレンダーですがいつも通り書いていきます。今回はpythonで数独を解いていこうと思います。
※コードはこちらに挙げておくので主要なコードのみ説明します。
数独のルール
- あいているマスには1から9までの数字が必ず1つ入る。
- 縦9マスに1から9までの数字が1つずつ入る。(重複はしない)
- 横9マスに1から9までの数字が1つずつ入る。(重複はしない)
- 太線で囲まれた3×3のブロックのどれにも1から9までの数字が1つずつ入る。(重複はしない)
実装
今回は最適化問題でよく使われるmypulpモジュールを使います。データはエクセルに格納しopenpyxlを使い扱います。必要なモジュールはrequirements.txtに格納しておいたので下記コードをコマンドラインで実行してください。
pip install -r requirements.txt
データ作成
まず数独のデータを保管するリストを用意します。
N = [i for i in range(1,10)] #行番号,列番号,数
C = [(3*i+2, 3*j+2) for i in range(3) for j in range(3)] #ブロックの中心位置の集合
D = [(i-1, j-1) for i in range(3) for j in range(3)] #周囲8マス+そのマスの相対的な位置の集合
そしてエクセルからヒントの数を読み込みます。
n = {}
for i in N:
for j in N:
n[i, j] = sheet.cell(row=i+1, column=j+3).value
制約条件
制約条件は主に四つ挙げられます。
① 何かしらの数字が入る(ヒントの数字含む)
for i in N:
for j in N:
if type(n[i, j]) is int and 1 <= n[i, j] <= 9:
model.addConstr(x[i,j,n[i, j]]==1)#ヒントの数字
else:
model.addConstr(quicksum(x[i,j,k] for k in N)==1)#それ以外
② 行に各数字が1つずつ入る
for i in N:
for k in N:
model.addConstr(quicksum(x[i,j,k] for j in N)==1)
③ 列に各数字が1つずつ入る
for j in N:
for k in N:
model.addConstr(quicksum(x[i,j,k] for i in N)==1)
④ ブロックに各数字が1つずつ入る
for (ci, cj) in C:
for k in N:
model.addConstr(quicksum(x[ci+di, cj+dj, k] for (di, dj) in D)==1)
目的変数
通常最適化問題では何らかの数値を最大、最小にすることが多いですが今回は特にありません。
実行
今回はsudoku_ans.xlsxという別のファイルに書き込むようになっています。
model.optimize()
# 出力
if model.Status == GRB.Status.OPTIMAL:
print('解が見つかりました。')
for i in N:
for j in N:
for k in N:
if x[i, j, k].X > 0.01:
font = copy(sheet.cell(row=i+1, column=j+13).font)
if type(n[i, j]) is int:
font.color = styles.colors.Color(rgb='ffff0000') #ヒントの数
else:
font.color = styles.colors.Color(rgb='ff000000') #求めた数
sheet.cell(row=i+1, column=j+13).font = font
sheet.cell(row=i+1, column=j+13).value = k
book.save('sudoku_ans.xlsx')
else:
print('解が見つかりませんでした。')
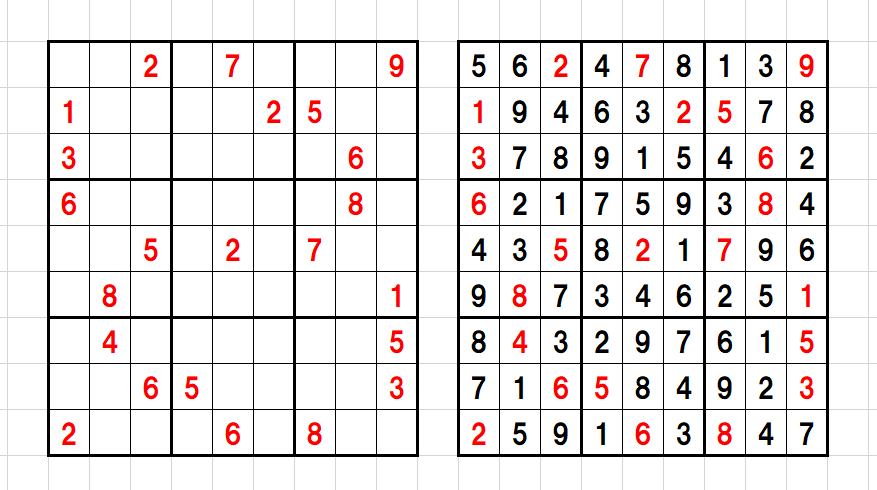
最後にsudoku_ans.xlsxを確認ししっかり数が入っていれば成功です。
まとめ
今回は数独を解きましたが、数学パズルゲーム全般解けるのでいろいろ試してみたいですね。それでは😇