はじめに
皆さん、当たり判定 はご存知ですか?
主にゲームや物理シミュレーションで行われる、「二つのオブジェクトが衝突しているかどうか判定する」アルゴリズムのことです。
当たり判定には色々ありますが、有名なものに GJKアルゴリズム があります。
これは、凸型(簡単に言うと凹みがない)多角形(ポリゴン)なら何でも当たり判定が出来てしまうアルゴリズムです。
その GJKアルゴリズム の コア として、 ミンコスキー差 が登場します。
ミンコスキー差って?
ミンコスキー差は、まず言語で説明すると「二つのポリゴンの中身にある座標(位置ベクトル)を全部引き算した後の図形 」を言います。
例えば、ポリゴン0とポリゴン1のミンコスキー差を出すとします。
ポリゴン0の中に含まれる座標(位置ベクトル)がありますね。
ポリゴン1にも。
これらを 全ての組み合わせにおいて 引き算します。
つまり、ポリゴン0に内包される位置ベクトル全てを
P_0 \in \vec p_{0, i} (i=0, \cdots)
ポリゴン1に内包される位置ベクトル全てで
P_1 \in \vec p_{1, j} (j=0, \cdots)
引き算
p = []
for p0 in P0:
for p1 in P1:
p.append(p0-p1)
#p全てあわせてミンコスキー差の図形
した図形が、 ミンコスキー差 (上記のpで構成される新たな図形)です。
ミンコスキー「差」ですが、扱っているのが位置ベクトルの集合なので、ミンコスキー差は図形を表現しているわけです。
どうして当たり判定?
ミンコスキー差は当たり判定にとても有効に使えます。
というのも、
ミンコスキー差の図形が原点を内包していれば、衝突している という定理があります。
まあこれはちょっと考えればで、原点を含むということは
p=[0,0,0]
を含んでいる。
pは先ほどの通りp = p0 - 01なので
要するに、これがp0 == p1を指しているわけです。
これで、
図形vs図形
のお話を
図形vs原点
の問題にすり替えることが出来るのですね。
もちろん、愚直にミンコスキー差を算出するのは計算量がかなり大きすぎるので、GJKアルゴリズムではベクトルの内積を上手に利用することで、ミンコスキー差の輪郭をとっています。
これについて、後々の記事でご紹介します。
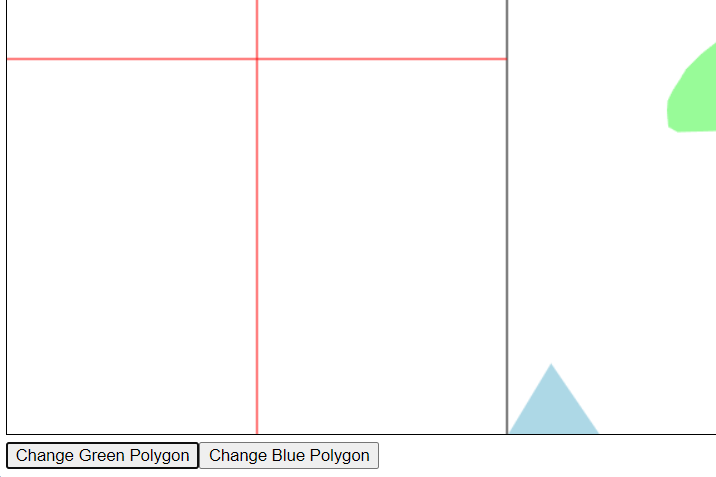
可視化した
PCならマウスを動かすだけ、スマホならタッチで、青の図形がその場に移動し、左側の画面で緑と青の間のミンコスキー差が可視化されています。
気づきにくいですが、Canvasの下にボタンがあり、これを押すと他のプリセットのポリコンに切り替わります。
使用ライブラリは我が自作ライブラリHotSoupScriptです: 初心者向けゲームプログラミングJavaScriptライブラリを作り、講座をした
仕組みは単純で、単純にCanvas内の全点(10ピクセルごとの間隔で)を走査することで、両図形に内包されている位置ベクトルを算出。
それらを引き算して、出てきたベクトルで新たに赤い四角を書いただけです。
分かること
衝突しているとき、原点を含む
逆に、 衝突していないとき、原点を含まない ですね。
凸図形同士のミンコスキー差は凸図形
(この組み合わせの)凹図形同士ならミンコスキー差は凹図形になっていますね。(この組み合わせ以外ならどうなるかは未調査です)
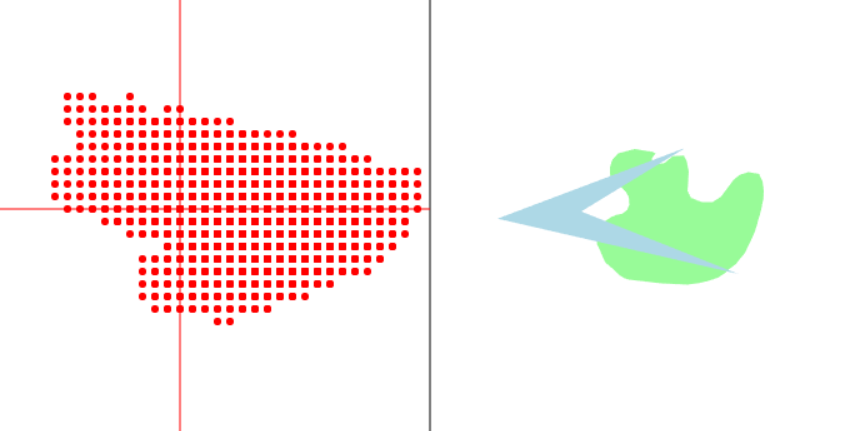
「 凸図形同士ならミンコスキー差は凸図形 」はGJKアルゴリズムが前提とする定理になっています。
証明はそんなに難しくないのですが、検索すればすぐ出てくるので割愛。
図形が平行移動だけならミンコスキー差も平行移動
いつ使うか分かりませんが、図形が回転せず平行移動するだけなら、ミンコスキー差が変形せず、そのまま平行移動することがわかりますね。
最後に
弊HotSoupScriptライブラリは描画APIを単純化していてこういったビジュアルプログラミングに扱いやすいのでオススメです: https://github.com/konbraphat51/HotSoupScript
GJKアルゴリズムの記事、そのうち投稿します。
いいね頂けると泣いて喜びます><
この記事を読んでいる方は次の記事を読んでいるかもしれません:


