高校物理の運動方程式を知っていればこの記事は不要です
この記事は
- 高校物理を習っていない中高生(and方程式を理解できる小学生)
- 高校物理を避けてきた文系の方
- やったはずだけど全然覚えてないor加速度を意識せずに
AddForce()を使おうとしている御方がた
向けの記事です
AddForce()は「移動」じゃない!
どうしてか、初心者向けのUnityプログラミングの教科書、ネット記事などなどには、「移動」として、説明もなしに AddForce() を使うものと決めつけているものが多くあります。
しかし、AddForce()は「移動」ではありません。 「力(Force)を加える(Add)」 関数(メソッド)です。(そのまま)
Unityを使っておらず何のことか分からない人へ
Unityには物理をシミュレーションしてくれる機能があります。
現実のように物体がぶつかってぶっ飛んだり、重力で落下したりすることを自動で再現してくれます。
そこで、AddForce()という、単純に力を作用させる関数が存在し、なぜかなりふり構わず頻繁に使われています。
もし皆様お使いのエンジンに 力を加える関数 があれば、AddForce()をそちらと置き換えてご覧ください。
思考停止でAddForce()を使っていると、このような問題が発生しませんでしたか?
- 速度を思い通りに制御できない
- 一定速度で移動したいのに、なんかめっちゃ加速してしまう
- 一度動き出したら止め方が分からない
運動方程式 を意識せずにAddForce()を使ってしまうと、訳もわからずこのような挙動に悩まされるでしょう。
(東大文系の人もこのような事態に悩んでいましたので、何も恥じる必要はないですヨ。
逆に東大理系の僕は県庁所在地の穴埋めプリントを未だに埋められないので。)
運動方程式って?
なるべく誰でもわかるように説明しますが、それを読むのがめんどくさければ、最後の「結論」をみてください。
まずは、運動方程式をお見せします。
F=ma
- $F$は力
- $m$は質量 (「重さ」と言ったら物理学のオタクに怒られますが、まあ「重さ」です)
- $a$は加速度(下で説明します)
です。
ニュートンの古典力学(高校で学ぶ物理)では、 この世の物体全てがこの方程式通りに動く とされています。
読まなくて良い話
物体の速度が光速に近かったりと、とんでもない例外は運動方程式に従わないので、アインシュタインが編み出した量子力学と相対性理論で構成される「現代」物理学の方が「正確」であると言いますが、我々がゲームで扱うのはそんなイレギュラーなものとは程遠いので、古典力学で「十分」なのです
読まなくて良い話2
偉大な物理学者ニュートンが、天体の動きから、この方程式・法則を「発見」(≠証明)しました。
もし「どうしてこんな法則が成り立つの?」という疑問があれば、その答えは「なんか17世紀のオタクが立てた仮説がたまたま世界の仕組みとだいたいマッチしていた」というだけです。
加速度って?
初心者にはまず加速度の説明をしなければいけませんね。
過去の記事から自己剽窃をします。
加速度$a$は速度の速度です
もし、速度が$3km/h$だと、「1時間後に3km移動している」という意味ですよね。
加速度が$3km/h^2$だと、「1時間後に 速度が 3km/hだけ速くなっている」という意味です。
簡単ですね。
引用:【ゲーム物理】離散要素法DFMで簡単力学シミュレーション!① 基礎編
もしこれで理解できなさそうな場合は、こちらの方がもっとフレンドリーです: https://www.yukimura-physics.com/entry/dyn-f05
運動方程式ってどういう意味?
数式は言葉です。計算じゃない。
僕が大好きな苑田尚之師の、大好きな言葉です。
物理で出てくる数式というのは、英語や日本語以上に「意味」を的確に、豊富に表しています。
力がなければ、加速しない
$F$に$0$が入ったらどうなりますか?
0=ma
こうなりますね。
ところで、皆さんが扱っている物体は 質量$m$が$0$になるわけがないです
なぜなら、どんな物体も原子で構成されている以上、その原子の質量が必ず存在するからです。
なので$m>0$です。
読まなくて良い話
実在する質量0の物質には、光子(フォトン)が知られています
では$ma$が$0$になる筋道は?
$a=0$と決定されますね。
方程式を解くのに不慣れな人へ
\displaylines{
0 = ma\\
m > 0 \Rightarrow m \neq 0
}
と今までの説明で分かっています。
$m$は$0$ではないことだけはわかっているので、 適当に $m=100$とかにして
0 = 100 \times a
が成立するには、 $a=0$しかない、ということです。もし納得かなければ、この方程式が成り立つ$a$を$0$以外に探してみてください。ないので。
AB=0について
$AB=0$のとき、$A=0$or$B=0$のどちらか、あるいは両方が必ず成立します。(中学数学!)
日本語で表すと
力(F)がなければ(=0)、加速度(a)がない!(=0)
ということです。
ここから2つの具体例を挙げることができます。
静止した物体は急に動き出さない
みなさまの周りにティッシュ箱はありますか?それを目の前の机においてください。置いたら、手を触れないで観察してみてください。
急に動き出しました?動きませんよね?
しかし、手で叩いてみてください。ぶっ飛びましたよね?
止まっている物体は、力がない限り動かない
ということです。
加速度がずっと0なので、速度が変わらない、ということですね。
じゃあ坂道にボールが置いたらどうして転がるか。
もちろん、それは「重力」を受けているからです。
ティッシュ箱も重力を受けているじゃないかって?その通りです。
もし重力 だけ を受けているのであれば、運動方程式にしたがって、物体は下向きの加速度を受け、つまり下へ動くはずです。しかし、それでは机へめり込んでいってしまう。
物体同士めりこまないように、 物体が物体を押しのける力として、垂直抗力 があります。
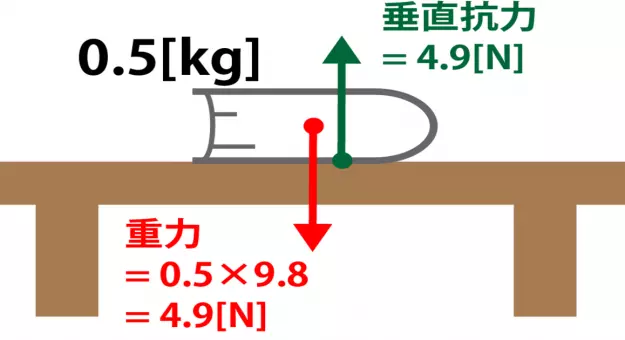
引用:受験のミカタ 垂直抗力とは?垂直抗力の求め方をイラストで徹底解説!
この場合なら、本が重力により机にめりこまないように、机が本を押している。その押す力が垂直抗力です。
重力と垂直抗力が殺しあっています(つりあいます) ので、 Fが最終的に0になります
式で説明すると、
$F=重力-垂直抗力=0$
ということです。
坂道の場合
三角関数$sin$, $cos$が図に出てきますが、数学アレルギーの皆様は目を逸らしてください。
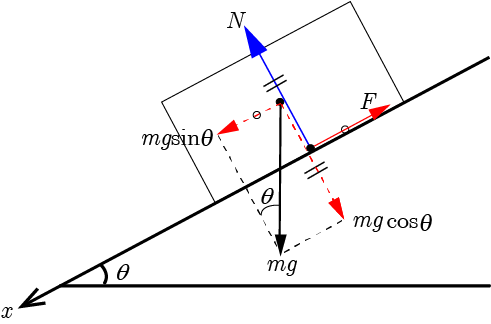
引用:KIT物理ナビゲーション「垂直抗力」
ここでの 垂直抗力 は $N$ の青い矢印です。 垂直 なので、この方向になります。(接触面に垂直)
そして、重力は $mg$ の黒い矢印です。
この青い$N$の矢印と、黒い$mg$の矢印が殺し合うとどうなるか。
ここで$N$の矢印見てください。ちょっと左にそれていますね。 $mg$の矢印はその左向きの成分を殺すことはできない。
よって、 完全に消しあうのではなく、$N$のせいで左向きの力が余る ことになります。
それが図の$mgsin\theta$の赤い点線矢印です。
こいつのせいで、坂道方向に滑り落ちます。
ちょっとだけ傾いた場合は滑らずにその場に居続けるのではないかって?
それは「摩擦力」のせいで、この図の$F$に当てはまります。
飛んでいる物体は、力がないとそのまま動く
ここは 直観的には分かりづらいところです。
宇宙空間でボールを投げてみてください。そのボールが$100km/h$で飛んだとしましょう。
そのボールは、他の力を受けない限り、ずっと$100km/h$で、ずっと一直線で、飛び続けます。永遠に。
前述の通り、 加速度は$0$なので、速度が変わることはできません
速度が変われないので、 減速もできず、方向も変わりません(方向が変わるということは、別方向への速度が追加される、ということ)
我々が地球上で投げたボールは、ちょっと減速しますね。これは 空気抵抗という力を受けているからです。
逆に、ゲーム上でこれを再現したい方は、空気抵抗で減速するというシミュレーションの実装を追加しないといけません。
力を受けている間は、加速する
力を受けている、つまり$F \neq 0$です。上の逆ですので、$a \neq 0$とわかります。
丁寧な解説
力を受けているので$F \neq 0$ですよね。
上記の解説により、$m > 0 \Rightarrow m \neq 0$もわかっています。
F=ma
において、仮に$a=0$だと$F=0$になって矛盾しますね。
なので$a \neq 0$とわかります。
すなわち、力をずっと加え続けていると、無限に加速する、ということです。
結論
- 静止した物体は急に動き出さない
- 飛んでいる物体は、力がないとそのまま動く
- 力をずっと加え続けていると、無限に加速する
ことがわかりました。
AddForce()の注意
「力を加える」ということは、「加速度を与える」ということ
運動方程式により、 「力を加える」ということは、「加速度を与える」ということがわかりました。
なので、AddForce()の使い方によっては、このような問題に直面するでしょう
毎フレームAddForce()を使う
UnityではUpdate()の中でAddForce()を使う場合ですね。
もうお分かりの通り、ずっと加速するので、時間が経てば経つほどとんでもない速度になります。
もし移動することが目的であれば、制御できないので 継続的なAddForce()はやめた方がいいですね
動き出しにAddForce()を使う
移動の最初のフレームだけ AddForce() を使うパターンですね。 これも制御しづらいと思います。
というのは、最初に加速して、速度が生まれて、そのあと(慣性に任せて)放置しているので、例えば何かにぶつかったときの挙動などを制御する処理を実装しなければいけません。
また、例えば左に行っていたところを右に転換したかったら、左移動の分の速度を打ち消して、かつ右移動の加速度を生まねばならないので、なおさらめんどくさい。
AddForce()は力を加えたいときに使うべき
関数名そのままですけどね。
例えば
- 磁石から磁力を受けて、吸い込まれていく挙動
- 空気抵抗を受けて減速する
- 攻撃を受けてぶっとぶ
など、 「力を加えられた」ことを演出したいときに AddForce()を使うべき であることを主張します。
移動のためにAddForce()を使うのは難しいです。
ベストプラクティスは?
加速度ではなく、速度を扱う
加速度が扱いづらいことは上記の説明で分かると思います。
「速度」を使いましょう。
Unityの場合は、RigidBody.velocityがありますね。
これなら毎フレーム指定し続けても変な暴走はしませんし、制御しやすいです。
座標をそのまま加算する?
RigidBodyを使わない場合は、transform.positionに加算することも考えられますが、当たり判定を考慮する場合は「めりこみ」に注意する必要があります。
参考:Unityでプレイヤーを移動させるときは、本当にAddForceが良いのか
ちなみに、この場合の実装上の注意点に関してはこちらをご覧ください:
【ゲームプログラミング】「速度」を使う時は必ずdeltaTimeを使ってください
最後に
もしこちらの記事を見て、ゲーム作りをする上では物理から逃げられないな、物理勉強しないといけないかな、と思われた方は、こちらがオススメです:
橋元の物理基礎をはじめからていねいに
橋元の物理をはじめからていねいに【改訂版】力学編
(物理基礎→力学編 という順番で読まなければなりません)
僕は何も知らない中学3年生でこちらを読んで、高校物理が大好きになりまして、そこそこの大学の入試なら大体なんでも解けるようになりました。
この橋元先生は力学をかなり シンプル で 機械的に 理解できるように整理していますので、最高です。(本のレイアウトや書き方もとても優れています)
最強になりたければメルカリで苑田師のノートを買ってください。
タイトルの「【東大生が解説】」について、実験的にこれを差し込むとどう反響が変化するのか実験的に入れているものであり、恥ずかしさとみっともなさでかなり心が苦しいです。
やっぱり無理なので消しました
いいね頂けると泣いて喜びます><
この記事を読んでいる方は次の記事を読んでいるかもしれません: