【3Dプログラミング】多数の直線を最小の動きで一点交差させる

このレポジトリのお話をします：https://github.com/konbraphat51/line_minimum_interception
パッケージ化しているので、そのまま関数をimportして使えるはずです。

はじめに

このように、ねじれの位置にある複数の直線（青色）を、なるべく最小の動きで（緑色がそのベクトルを表す）、一点で交差（赤色）させる手法を紹介します。

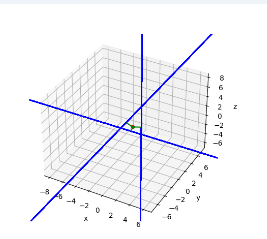
複数の物体認識情報からの立体視、ロボットアニメなどで奇跡的にビームライフルが一点で交差して相殺しあう演出をゲーム上で無理矢理したい、その他ニッチなタスクに使えるのではないでしょうか。

あるいは、ベクトルの扱い、最適化計算の扱いに慣れるための題材にちょうどいい難易度かもしれません。

理論

かなり簡単です。簡単なことを、長々と説明します。

3D空間上の直線は、高校の数学でやる通り

• 自由度1の等式で表現（要するに方程式2つ分; $x-1=y+2=z+3$）
• 始点からの方向ベクトルの伸びで表現$\overrightarrow{start} + t \times \overrightarrow{direction}$

の2通りがありますね。

ゲームプログラミングの人間なのでベクトルを使います。

方針

後述する前提1, 前提2を利用しながら、高校数学的に「全ての直線が一点で交わる条件」の連立方程式が求められます。

そして、我々が欲しいのは「最小の動き」なので、移動量を最小にすればよいです。
最適化の出番ですね。

前提1; 直線の移動は法線だけ考えればいい

直線は定義上 無限に 伸びている線です。

なので、極端な話、この黒の直線を、青の矢印方向に移動させても変わりません。

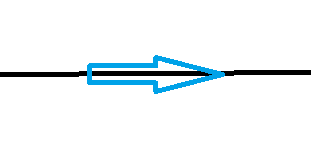
これと同じ理屈で、この青の矢印と赤の矢印は同じ上方向への移動を表しますね。

すなわち、直線に 平行な成分は無視できます

なので、直線の法線方向への移動だけを考えればいいです。

前提2; 直線の移動ベクトルは、直線の法線ベクトル2つで表せる

法線ベクトルといっても、360度大量にあります

しかし、これらは全て同一の平面上にあるので、2つの独立なベクトルと2つのパラメーターを付け加えることでありとあらゆる移動パターンを表現できます。（高校数学）

直線を$l$として、法線ベクトル$\vec h_0$, $\vec h_1$を使い
$\overrightarrow{movement} = H_0 \cdot \vec h_0 + H_1 \cdot \vec h_1$
と表せるわけです。

「全ての直線が一点で交わる条件」の連立方程式

直線$i$の上にある位置ベクトルは、始点を$\overrightarrow{movement}$分ずらして、

\displaylines{
(\overrightarrow{start}_i +\overrightarrow{movement}_i) + t_i \cdot \overrightarrow{direction}_i \\ = \overrightarrow{start}_i + H_0 \cdot \vec h_{i, 0} + H_{i,1} \cdot \vec h_1 + t_i \cdot \overrightarrow{direction}_i 
}

について、$H$と$t$を自由に動かせます。

これら全てが一点で交わるとき、その一点は、

\displaylines{
\overrightarrow{start}_i + H_0 \cdot \vec h_{i, 0} + H_{i,1} \cdot \vec h_1 + t_i \cdot \overrightarrow{direction}_i |_{i=0}\\
=\overrightarrow{start}_i + H_0 \cdot \vec h_{i, 0} + H_{i,1} \cdot \vec h_1 + t_i \cdot \overrightarrow{direction}_i |_{i=1}\\
= \cdots \\
= \overrightarrow{start}_i + H_0 \cdot \vec h_{i, 0} + H_{i,1} \cdot \vec h_1 + t_i \cdot \overrightarrow{direction}_i |_{i=last}
}

が我々の連立方程式になり、全ての$H$と$t$を求めればいいわけです。

移動量の最小化

最小二乗法で$\sum|\overrightarrow{movement}_i|^2$を最小化。ただそれだけ。

実装

図形の表現

まずは何回も書きすぎてもはや暗唱しているまでもあるベクトルクラスの実装から：

GeometryExpressions.py

class Vector:
    """
    3D Vector
    """

    def __init__(self, x: float, y: float, z: float) -> None:
        """
        Set vector components
        各成分を初期化

        :param float x: x component
        :param float y: y component
        :param float z: z component
        :rtype: None
        """

        self.x = x
        self.y = y
        self.z = z

    def __add__(self, other: Vector) -> Vector:
        #足し算
        return Vector(self.x + other.x, self.y + other.y, self.z + other.z)

    def __sub__(self, other: Vector) -> Vector:
        #引き算
        return Vector(self.x - other.x, self.y - other.y, self.z - other.z)

    def __mul__(self, sc: float) -> Vector:
        #掛け算（スカラー右）
        return Vector(self.x * sc, self.y * sc, self.z * sc)

    def __rmul__(self, sc: float) -> Vector:
        #掛け算（スカラー左）
        return self * sc

    def __truediv__(self, sc: float) -> Vector:
        #割り算
        return Vector(self.x / sc, self.y / sc, self.z / sc)

    def __getitem__(self, index: int) -> float:
        #タプルのように添え字からも取り出せるように
        if index == 0:
            return self.x
        elif index == 1:
            return self.y
        elif index == 2:
            return self.z
        else:
            raise IndexError("Vector index out of range")

    def __str__(self) -> str:
        """
        for getting string expression when debug
        """
        return f"({self.x}, {self.y}, {self.z})"

    def calculate_length(self) -> float:
        """
        Calculate vector length
        長さ

        :return: vector length
        :rtype: float
        """

        return (self.x**2 + self.y**2 + self.z**2) ** 0.5

    def calculate_normalized(self) -> Vector:
        """
        Return normalized vector
        単位ベクトルに

        Doesn't modify the original instance.

        :return: normalized vector
        :rtype: Vector
        """

        return self / self.calculate_length()

    def calculate_cross(vector0: Vector, vector1: Vector) -> Vector:
        """
        Calculate cross product of two vectors
        外積

        This is static function

        :param Vector vector0: vector0
        :param Vector vector1: vector1
        :return: cross product of two vectors
        :rtype: Vector
        """

        return Vector(
            vector0.y * vector1.z - vector0.z * vector1.y,
            vector0.z * vector1.x - vector0.x * vector1.z,
            vector0.x * vector1.y - vector0.y * vector1.x,
        )

これを用いて、直線を表します。
始点の位置ベクトル、方向ベクトルの2種だけ覚えていれば大丈夫ですね。

GeometryExpression.py

class Line:
    """
    Line in 3D space
    """

    def __init__(self, start_position: Vector, direction: Vector) -> None:
        """
        Set attributes

        :param Vector start_position: start position
        :param Vector direction: direction
        :rtype: None
        """

        self.start_position = start_position
        self.direction = direction.calculate_normalized()

Vector, Lineの2つのクラスで図形を扱います。

前処理

理論はすでに説明したので、ギアを上げていきます。

整合性のあるコードが見たい場合は冒頭のレポジトリをご覧ください。

法線ベクトルを求める

外積を2回使うだけ。

first = Vector.calculate_cross(vector, dummy).calculate_normalized()
second = Vector.calculate_cross(first, vector).calculate_normalized()

連立方程式を用意

$A=B=C= \cdots = Y =Z$
は
$A=B \quad AND \quad B=C \quad AND \quad C= \cdots \quad AND \quad Y = Z$
と同じことを利用して、お隣さん同士の=一つの方程式に分解します

for cnt in range(len(lines) - 1):
    _compute_conditions(
        cnt,
        lines[cnt],
        normal_vectors[cnt],

        #一つ後ろのもの
        cnt + 1,
        lines[cnt + 1],
        normal_vectors[cnt + 1],
    )

動的に関数を用意するには、lambdaを用意すると解決します。

return {
    "type": "eq",
    "fun": lambda params: (
        (
            line0.start_position[component_id]
            + line0.direction[component_id]
            * params[_get_extension_param_position(id0)]
            + normals0[0][component_id]
            * params[_get_movement_param_position(id0, 0)]
            + normals0[1][component_id]
            * params[_get_movement_param_position(id0, 1)]
        )
        - (
            line1.start_position[component_id]
            + line1.direction[component_id]
            * params[_get_extension_param_position(id1)]
            + normals1[0][component_id]
            * params[_get_movement_param_position(id1, 0)]
            + normals1[1][component_id]
            * params[_get_movement_param_position(id1, 1)]
        )
    ),
}

最小化する目的関数

法線ベクトル同士が垂直なので、$\sum H^2$を求めるだけ（証明略）

def _compute_score(params: list[float]):
    """
    Compute the score of the parameters.

    This is sum of squares of the movement vectors.

    :param list[float] params: parameters
    :return: score
    :rtype: float
    """

    # square of the movement vector length
    score = 0
    for index in h_indices:
        score += params[index]
    return score

最小化

つっこむだけ

result = minimize(_compute_score, parameters, constraints=conditions)

これで一番良い$H$たちと$t$たちが求まりました。

後処理

移動ベクトル

$H_0 \cdot \vec h_0 + H_1 \cdot \vec h_1$を求めるだけ

# convert to Vector
movement_vector = (
    normal_vectors[line_id][0] * parameters[line_id][1][0]
    + normal_vectors[line_id][1] * parameters[line_id][1][1]
)

交差点

理論で説明した連立方程式は、一つ一つが交差点の位置ベクトルを表すため、1つ目を確認するだけで十分なのです。

intersection_point = (
        lines[0].start_position
        + lines[0].direction * parameters[0][0]
        + movement_vectors[0]
    )

完了です