概要

位相的データ解析(TDA)が気になったので、HomCloudで遊んでみた。

こんなのを作ります！

はじめに

TDAすげえ！　って思ったのがJSTのプレスリリースで見つけた以下の記事です。

記事の図1を見ればはっきりわかるように、ガラス(アモルファス)と液体の違いが明確に示されています。
これはすごい！！！！！

位相的データ解析とホモロジーの説明は、HomCloudを作成した研究室で公開されている解説スライドが非常にわかりやすいので、ぜひ見てみてください。
http://www.wpi-aimr.tohoku.ac.jp/hiraoka_labo/introduction_j.pdf
(内容はかなりタフだけど……)

というわけで、解析ソフトHomCloudを使って、パーシステントホモロジーの計算を行ってみました。

HomCloudの導入

こちらで公開されています。
HomCloud
導入方法は非常に丁寧に解説されているので、本記事では省略します。

環境はWindows Subsystem for Linux(WSL) + Ubuntuでやってます。
WSLのセットアップ・使い方に関してはこちらを参考にしました。
「Windows Subsystem for Linux(WSL)」セットアップガイド【スクリーンショットつき解説】
Windows 10のWindows Subsystem for Linux（WSL）を日常的に活用する

サンプルで遊ぶ

素晴らしくありがたいことに、HomCloudはチュートリアルも充実しています。
とりあえず、以下のサンプルで遊んでみます。
3次元点集合データ(ポイントクラウド)の解析

ただ、ここで以下のコマンド

python3 -m homcloud.plot_diagram -d 1 -l pointcloud.idiagram

でプロットを表示させようとしたところ、

_tkinter.TclError: no display name and no $DISPLAY environment variable

と怒られてしまいました。

解決できそうな感じですが、どのみち生データから自分で解析するつもりだったので、とりあえず無視して、txtで出力させてPythonでプロットします。
ヒストグラムなんでmatplotlibのhist2dを使って……

import matplotlib as mpl
import matplotlib.pylab as plt
dataset = pd.read_csv("pointcloud-pd1.csv")

fig=plt.figure()
ax = fig.add_subplot(111)
ax.set_aspect('equal', adjustable='box')
H = ax.hist2d(dataset["Birth"], dataset["Death"],bins=128,
              norm=mpl.colors.LogNorm(), cmap="rainbow")
L = ax.plot([0,1], [0,1], c="black", lw=1)

ax.set_xlabel('Birth')
ax.set_ylabel('Death')
fig.colorbar(H[3],ax=ax)

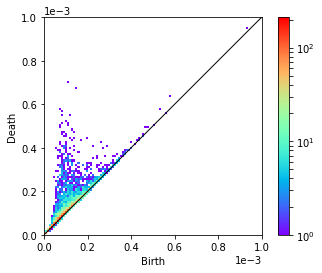
こんな感じに、チュートリアルと同じようにプロットできます！
(ちなみに、この図はパーシステント図と呼ばれます)

2次元データを自分で作って解析する

チュートリアルの図を自分で作ることはできたので、次はソフトに読ませる点群を自分で作成してみます。
さっきのは[-1, 1]×[-1, 1]×[-1, 1]の3次元領域に5000の点をランダムに置いていたので、今回は2次元領域[0, 1]×[0, 1]に5000点ぐらい撒いてみます。

import numpy as np
import pandas as pd
import random
x_list = []
y_list = []
for i in range(5000):
    x_list.append(random.random())
    y_list.append(random.random())
dataset = pd.DataFrame({'x':x_list,'y':y_list})
dataset.to_csv("random.csv", sep=" ", index=False)

こんな感じに作りま～す。
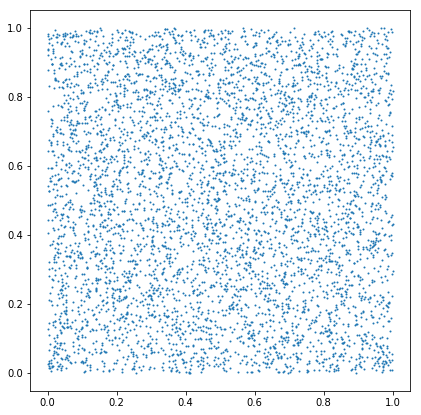
領域内の点をプロットすると以下のようになります。

ランダムだけじゃつまらないんで、三角格子っぽいのも作ってみることにします。

x = np.linspace(0,1,71, retstep = True)
y = np.linspace(0,1,71, retstep = True)
x_list = []
y_list = []
for num,i in enumerate(y[0]):
    for j in x[0]:
        if num%2 == 0:
            y_list.append(i + (random.random() *1.0E-3))
            x_list.append(j + (random.random() *1.0E-3))
        else:
            y_list.append(i + (random.random() *1.0E-3))
            x_list.append(j + x[1]/2)
dataset = pd.DataFrame({'x':x_list,'y':y_list})
dataset.to_csv("triangle.csv", sep=" ", index=False)

完全な三角形・四角形があると計算がエラーになることがあるらしいので、適当に値をばらつかせています。
この2つの点群を使って、パーシステントホモロジーを計算します。

計算結果

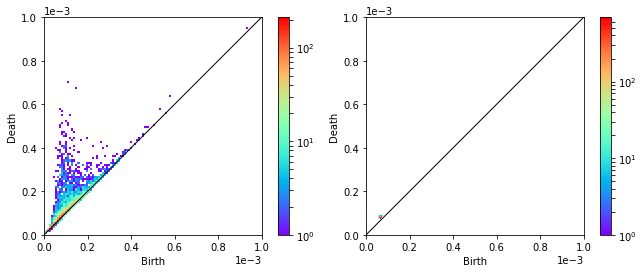
計算結果はこんな感じになりました。
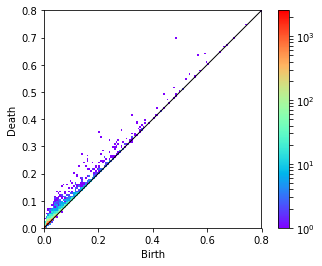
左がランダムな点群, 右が三角格子(ちょっとランダム)のパーシステント図です。

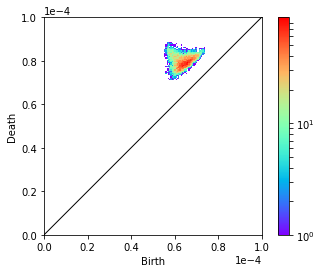
一見三角格子のほうは何もないように見えますが、拡大するとこんな感じです。

ランダムな点群では分布が広く、2次元的であるのに対して、周期性を持つ三角格子では分布が非常に小さく、ほぼ0次元的となっていることがわかります。

おもしろーい！

まとめ

以上、HomCloudを使ったパーシステントホモロジーの計算でした。
今回は自分で点群を2種類作成して、それぞれのパーシステント図をプロットし、点群の持つトポロジカルな情報を可視化してみました。

プレスリリースで参照していた論文では、アモルファスの原子構造をMD(分子動力学計算)で計算していたので、おおむね似たようなことをやっているのではないかと思います。

実際に固体中の原子の位置を一つ一つ知ることができればいいんですけどね……。
原子分解能の電子線トモグラフィーは既に実現されているみたいですが(参考)、これを一般的な材料に用いるのはかなり難しいと思われます。
とはいえ、夢が広がる解析方法であるのは確かなので、材料科学者の方々は覚えておくといいかもしれません。

あとは、みかんの皮にあるつぶつぶ(油胞)のように、自然界に存在する構造を解析するのも面白いかもしれないですね～。

それでは。

位相的データ解析(TDA)で遊んでみる

概要

もくじ

はじめに

HomCloudの導入

サンプルで遊ぶ

2次元データを自分で作って解析する

計算結果

まとめ