はじめに
この記事では、X線マイクロトモグラフィーで得られた断面画像をPythonを用いて解析する方法を解説します。
(透過像からの再構成ではありません)
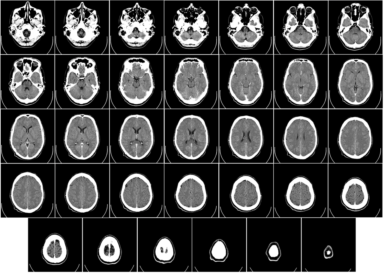
具体的には、下のような炭酸塩岩のμ-CT断面像を対象にして、
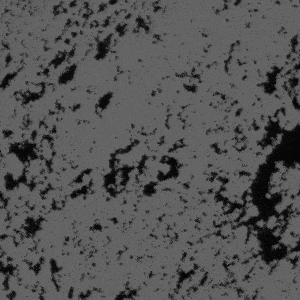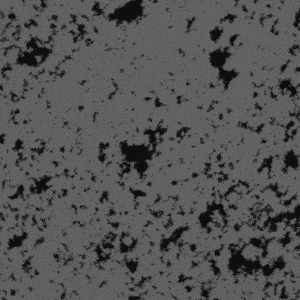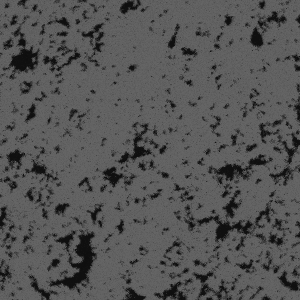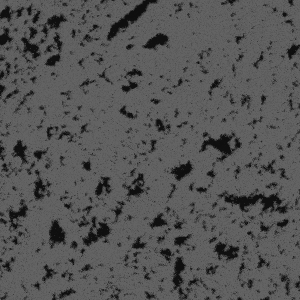
以下のように3次元的な連結性を考慮したセグメンテーションを行い、
最終的にこのような3次元像を得ます。
X線マイクロトモグラフィーとは？
おそらくQiitaを見ている人の99%が知らない手法だと思うので、簡単に解説します。
皆さん以下の装置はご存知ですよね。
(画像は https://jp.medical.canon/general/CT_Comparison より引用)
一般的に、この装置はCTという名前で呼ばれています。
CTというのはコンピュータ断層撮影(Computed Tomography)の略称で、X線を人体に照射して断面像を得る装置です。
人体を輪切りにしたような像が得られ、外から見えない内部構造がわかるのでとても便利です。
(画像は https://en.wikipedia.org/wiki/CT_scan より引用)
この「内部を見たい」という需要は当然人体以外にもあります。
例えば鋳物内部に空洞(巣)がどれぐらいあるかは外部からわかりませんが、巣は鋳造部品の特性に大きく影響するため、この手法での検査が有用です。
産業用途では、医療用とは異なり放射線被害をほぼ考慮しなくてよく、強力なX線を収束させて用いることができるため、高解像度の断面像が得られます。
このような手法がX線マイクロトモグラフィー(X-ray micro tomography)と呼ばれます。
X線トモグラフィーは非常に便利な手法です。
しかし、基本的に得られるのは先に示したように一連の断面画像です。
ここから、例えば空洞の3次元構造の解析等を行いたい場合は、専用のソフトを使うか、自分でプログラムを書く必要があります。
今回はこれをPythonでやります。
解析データのダウンロード
今回は、以下の論文で公開されている、炭酸塩岩のX線トモグラフィー像のデータセットを用います。
自由に使えるX線トモグラフィーのデータは意外に少ないので、このようにオープンアクセスの論文誌に公開されているのは非常にありがたいですね。
画像データは以下のサイトからダウンロード可能です。
今回は、上のサイトで公開されている"Rock-Reconstructed.raw"を解析に用いました。
だいたい845MBです(CT画像データとしては軽い方)。
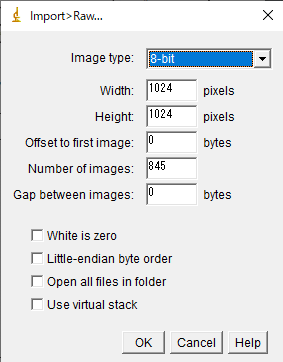
拡張子".raw"は見慣れない拡張子だと思いますが、皆さんご存知ImageJを使えばImage Sequenceとしてインポートできます。
File => Import => Rawでファイルを選択して、以下のように設定すればOKです。
(詳しくは論文内に説明があるので、別の画像を使いたい場合は確認してください)
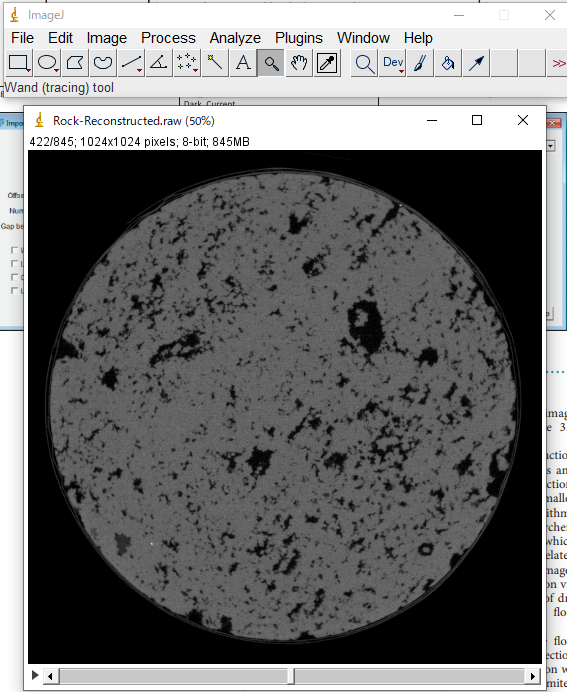
うまくいけば下のように画像が読み込めます。
あとは、File => Save As => Image Sequenceで適当なフォルダに保存してください。
OpenCVによる画像解析
これで、X線マイクロトモグラフィーで得られたデータが一連の画像として保存できました。
次は、OpenCVでノイズ除去や2値化を行います。
今回は、画像の中心部だけを解析することにします。
import numpy as np
import matplotlib.pyplot as plt
import cv2
import glob
# 画像パスの読み込み
path = glob.glob('./Rock-reconstructed/*.tif')
# 画像の読み込み
images = []
for n,i in enumerate(path):
img = cv2.imread(i,0)
images.append(img[100:400,100:400])
読み込んだ画像の例を下に示します。
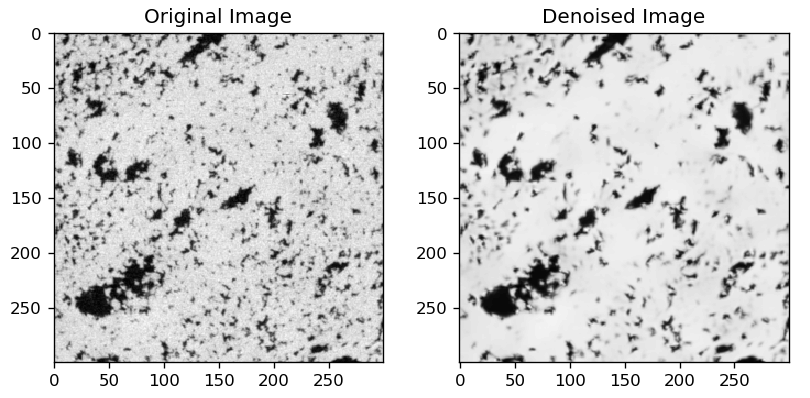
正直かなりきれいな画像なので必要ないのですが、一応ノイズ除去をしてみます。
OpenCVのNon-local means denoisingを用います。
# Non-local meansを使ったノイズ除去
test = images[200]
dn_test = cv2.fastNlMeansDenoising(test,None,10,7,21)
ノイズ除去なしとありの比較を下に示します。
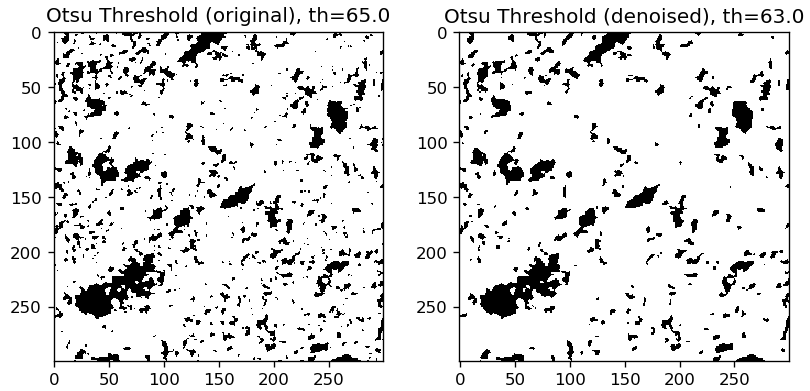
OpenCVを使った二値化は以下のようにやります。大津の自動二値化を使います。
# オリジナル画像を大津の方法で二値化
th,th_test = cv2.threshold(test,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
ノイズ除去ありと無しの比較はこんな感じ。
細かい穴が消えてしまってるので、ノイズ除去は余計かな……。
今回は無しでいきましょう。
この処理を一連の画像にまとめて適用します。
ついでにcv2.findContoursで領域を抽出してから、10px以下の空洞を除外します。
th_denoised = [] #このリストに画像を入れる
for i in images:
# ノイズ除去(今回はなし)
#dn = cv2.fastNlMeansDenoising(i,None,10,7,21)
# 二値化
__,th_dn = cv2.threshold(i,0,255,cv2.THRESH_BINARY_INV+cv2.THRESH_OTSU)
# 空洞領域の検出
i__,cnts,__ = cv2.findContours(th_dn,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)
# 空洞領域のうち、25px以上のものだけを抽出
img = np.zeros_like(i).astype(np.uint8)
for cnt in cnts:
if(cv2.contourArea(cnt) > 10):
img = cv2.drawContours(img, [cnt], 0, 255, -1)
# リストに追加
th_denoised.append(img)
cc3dによる連結領域のラベル付け
これで、断面像中の空洞領域を得ることができました。
次に、3次元的な連結構造を考慮して、連続した空洞をラベル付けしていきます。
これには connected-components-3d というライブラリを用います。
詳しいアルゴリズムに関しては上のページを参照してください。
pipを用いて以下のようにインストールできます。
pip install connected-components-3d
ラベル付けは非常に簡単です。しかも早い。
import cc3d
connectivity = 6
th_denoised = np.array(th_denoised)
labels_out = cc3d.connected_components(th_denoised,connectivity=connectivity)
connectivityは同一領域とみなすために必要な近接ボクセルの数を示しています。
たとえば6の場合は、x,y,zのそれぞれの方向に±1の隣接ボクセルを参照します。
6の他には、18, 26が選べるようです(ドキュメント参照)。
それぞれの画像のピクセルに対して、領域ラベルに対応する番号が1から振られていきます。(0は背景です)
そのため、例えば領域数は以下のように得られます。
#領域数を出力
numbers = np.max(labels_out) - 1
print(numbers)
>> 10001
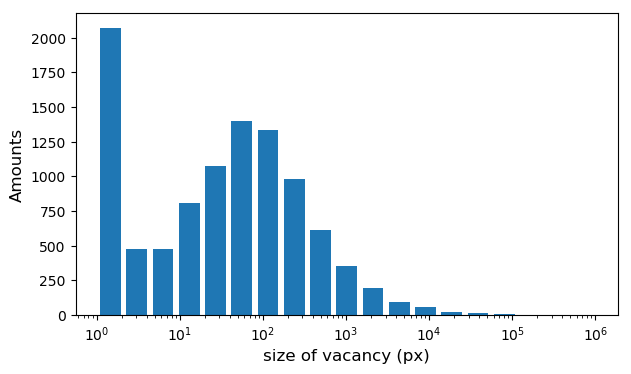
では、空洞の大きさの分布をみてみましょう。
以下のように解析できます。
# 空洞体積の計算
areas = []
for num in range(np.max(labels_out)):
count = np.count_nonzero(labels_out == num)
areas.append(count)
# 分布の表示
fig = plt.figure(figsize=(7,4),dpi=100,facecolor='white')
plt.hist(areas[1:], bins=np.logspace(0, 6, 20),rwidth=0.8)
plt.xscale('log')
plt.xlabel('size of vacancy (px)',fontsize=12)
plt.ylabel('Amounts',fontsize=12)
plt.show()
結果はこんな感じ。X軸は対数にしています。
どうやら空洞体積(ピクセル数)の分布は対数正規分布で表せるようですね。
具体的なサイズで表すためには、画像のスケールとz方向のスライス幅の値が必要になります。
空洞領域をRGBで色を付ける
このように、cc3dを用いると簡単に空洞領域の分離と解析ができます。
ただ、画像として見るときには、領域ごとにRGBで色分けした方が見やすいですよね。
これを行うプログラムを以下に示します。
import random
## それぞれのラベルに対応したRGBカラーをランダムに選択
param_list = np.linspace(0,np.max(labels_out),np.max(labels_out)+1,dtype=np.uint16)
color_list = {}
for i in param_list:
if(i != 0):
color_list[str(i)] = [random.randint(0,255),
random.randint(0,255),
random.randint(0,255)]
else:
color_list[str(i)] = [0,0,0]
## それぞれの空洞領域を色付け
void_colored = []
for img in labels_out:
h,w = img.shape
img_flat = img.flatten()
img_colored = np.zeros((img_flat.shape[0],3),dtype=np.uint8)
non_zero_idx = np.where(img_flat != 0)
for n in non_zero_idx[0]:
img_colored[n] = color_list[str(img_flat[n])]
void_colored.append(img_colored)
void_colored = np.array(void_colored)
void_colored = void_colored.reshape(void_colored.shape[0],h,w,3)
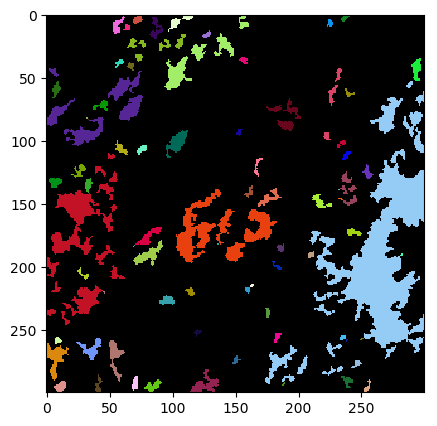
## 鋳巣領域が正しく色付けされているかを確認
fig = plt.figure(figsize=(5,5),dpi=100,facecolor='white')
plt.imshow(void_colored[0])
plt.show()
# 画像を保存
for num,img in enumerate(void_colored):
name = str(num).zfill(4)
cv2.imwrite('./labbeled_rock/'+str(name)+'.png',img)
このように色付けした領域は以下のようになります。
ImageJによる3次元表示
3次元表示にもPythonを使いたいところですが、いまいち良い方法が見つからないので、ImageJを使ってやります。
先ほど保存した色付け領域の画像をImageJ => File => Import => Image Sequenceで読み込みます。
読み込んだ状態でPlugins => Volume Viewerで3次元表示ができます。
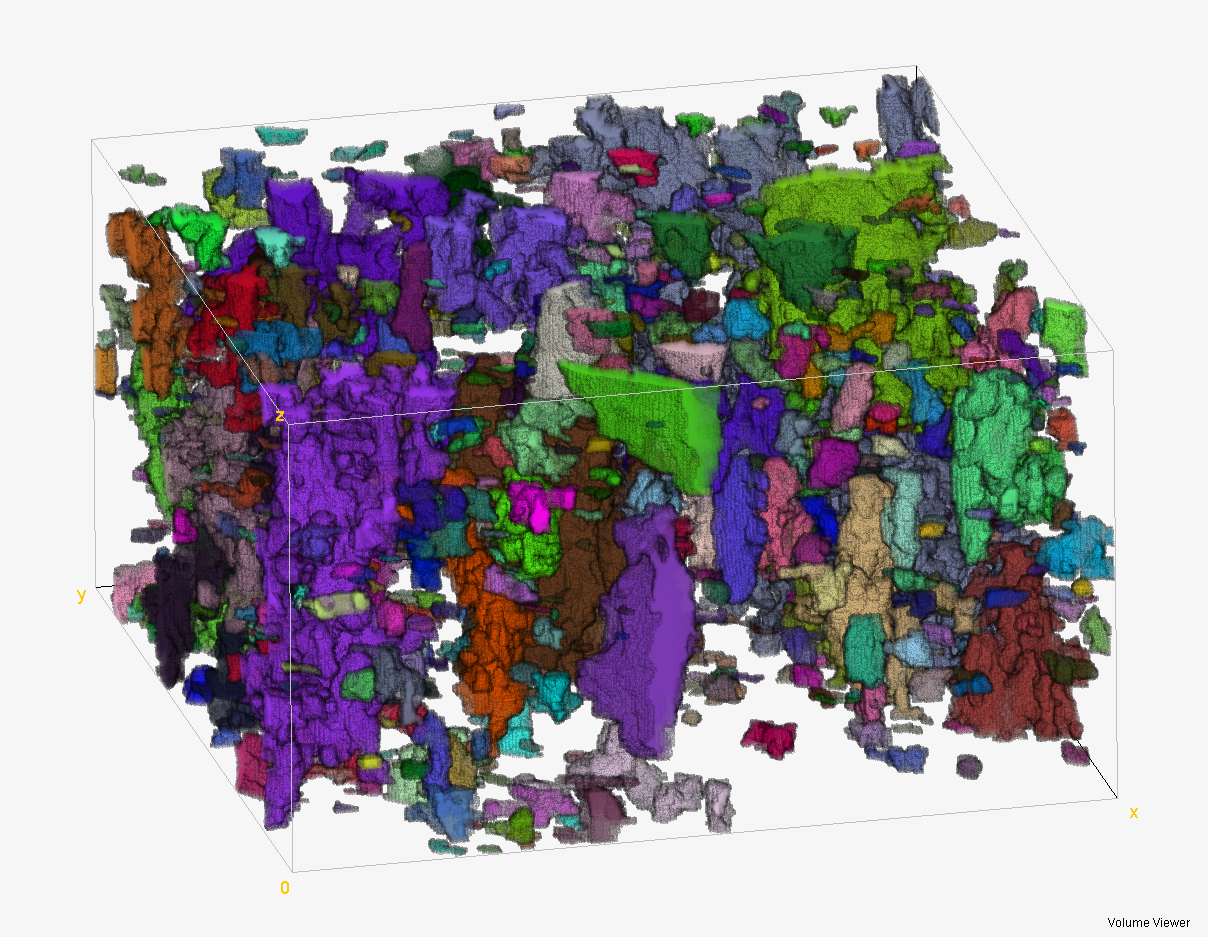
Z方向のスライス幅が分からないので、適当に縮尺を調整して3次元表示した結果が以下になります。
ぱっと見た感じ、きちんと連結した空洞領域が同じ色でラベル付けされていることが分かります。
うまくいってますね！
最後に
身近にX線トモグラフィーの解析をやっている人がいてちょっとお手伝いしたので、その備忘録がてら書いてみました。
今回はまじめに材料系の研究者らしい記事ですね。
あまりにニッチすぎてQiitaの読者層に刺さりそうにありませんが……。
お役に立てれば幸いです！