研究者のための実践データ処理～Pythonでピークフィッティング～

#はじめに
X線光電子分光(XPS)やX線回折法(XRD)などで得られたスペクトル状のデータを分析することはよくあると思います。
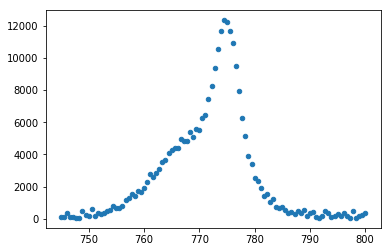
例えばこんな感じのデータとか。

(データは自作です)

最近の分析装置では、ピークフィッティングの機能は解析ソフトにくっついていることが多いです。
しかし、時には生データを自分で分析する必要に迫られることもあります。

そこで、上のように複数の分布が重畳したスペクトルを例にとって、Pythonを使って自動でフィッティングしてみます。

解析に使うサンプルデータはこちら。

#使用するパッケージ
解析にはJupyter-Notebook(Python=3.6.5,　scipy=1.1.0)を用いています。

%matplotlib inline
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import pandas as pd

#データの読み込み
今回解析に用いるデータは以下のようなcsvファイルになっています。

	x	y
0	745	141.0649622
1	745.5555556	105.1902807
2	746.1111111	378.0716102
3	746.6666667	108.3429052
4	747.2222222	115.5987665
5	747.7777778	58.82885972
6	748.3333333	57.74813435
7	748.8888889	499.8530406
8	749.4444444	238.6301071
          :          :

このデータをpandasで読み込んで、x, yそれぞれのカラムをリストとして取得します。
やり方は以下の通り。

dataset = pd.read_csv('sample.csv')
x = dataset['x']
y = dataset['y']

簡単ですね。

#フィッティング用関数の定義

今回のフィッティング関数にはガウス関数を用います。
ガウス関数とは、以下のような関数です。

y = a * exp\biggl(-\frac{(x-b)^2}{c^2}\biggr)

最適化するパラメータはa(amp), b(ctr), c(wid)の3つです。

フィッティングにはscipy.optimizeのcurve_fitを使います。
curve_fitでは関数を自分で作る必要があるので、以下のように定義します。

def func(x, *params):
    
    #paramsの長さでフィッティングする関数の数を判別。
    num_func = int(len(params)/3)
    
    #ガウス関数にそれぞれのパラメータを挿入してy_listに追加。
    y_list = []
    for i in range(num_func):
        y = np.zeros_like(x)
        param_range = list(range(3*i,3*(i+1),1))
        amp = params[int(param_range[0])]
        ctr = params[int(param_range[1])]
        wid = params[int(param_range[2])]
        y = y + amp * np.exp( -((x - ctr)/wid)**2)
        y_list.append(y)
        
    #y_listに入っているすべてのガウス関数を重ね合わせる。
    y_sum = np.zeros_like(x)
    for i in y_list:
        y_sum = y_sum + i
    
    #最後にバックグラウンドを追加。
    y_sum = y_sum + params[-1]
    
    return y_sum

ここで、関数にパラメータのリストをparamsとして与えています。
paramsの長さを3で割ったものが、フィッティングに用いるガウス関数の数になります。

フィットさせる関数の数が増えても対応できるように、ちょっと工夫をしています。

#プロット用関数の定義
関数の戻り値が足し合わせではなく、それぞれのガウス関数のリストになっています。
内容はフィッティング用の関数とほぼ同様です。

def fit_plot(x, *params):
    num_func = int(len(params)/3)
    y_list = []
    for i in range(num_func):
        y = np.zeros_like(x)
        param_range = list(range(3*i,3*(i+1),1))
        amp = params[int(param_range[0])]
        ctr = params[int(param_range[1])]
        wid = params[int(param_range[2])]
        y = y + amp * np.exp( -((x - ctr)/wid)**2) + params[-1]
        y_list.append(y)
    return y_list

#初期値の設定
ここがけっこう重要になります。
(初期値がおかしいとまともにフィッティングしてくれない)

サンプルのプロットを見る限りでは、2つのガウス関数でフィッティングできそうです。
今回は以下のように初期値を設定します

Peak1 = [4500, 760, 10]
Peak2 = [7500, 775, 10]

それぞれ、[強度(amp), 位置(ctr), 幅(wid)]となります。
さらに、バックグラウンドの強度として、background = 5を追加します。
これらをそれぞれ結合して、次のようなリストを作ります。

guess_list = [4500, 760, 10, 7500, 775, 10, 5]

コードにするとこんな感じです・

#初期値のリストを作成
#[amp,ctr,wid]
guess = []
guess.append([4500, 760, 10])
guess.append([7500, 775, 10])

#バックグラウンドの初期値
background = 5

#初期値リストの結合
guess_total = []
for i in guess:
    guess_total.extend(i)
guess_total.append(background)

これで、guess_listに初期値のリストが作れました。

#いよいよ関数でフィッティング

ここまで準備してしまえばフィッティング自体は非常に簡単で、下の一行でできます。

popt, pcov = curve_fit(func, x, y, p0=guess_total)

ここで、最適化されたパラメーターはpoptの中に入ります。
このときに、初期値の設定があまりにいい加減だと次のように怒られます。

OptimizeWarning: Covariance of the parameters could not be estimated
  category=OptimizeWarning)

このエラーが出たら、初期値の設定をいろいろと変えてみましょう。
どうしても合わないときは、関数の形を変えてみるのも手です。
(ローレンツ関数や、フォークト関数など...)

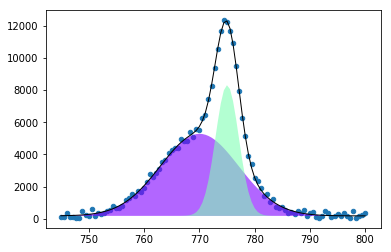
最終的にプロットまで行うコードは以下のようになります。

popt, pcov = curve_fit(func, x, y, p0=guess_total)

fit = func(x, *popt)
plt.scatter(x, y, s=20)
plt.plot(x, fit , ls='-', c='black', lw=1)

y_list = fit_plot(x, *popt)
baseline = np.zeros_like(x) + popt[-1]
for n,i in enumerate(y_list):
    plt.fill_between(x, i, baseline, facecolor=cm.rainbow(n/len(y_list)), alpha=0.6)

フィッティング結果のプロットは以下のようになります。

また、最適化されたパラメーターは以下の通りです。
それぞれ第1ピークの強度, 位置, 幅, 第2ピークの強度, 位置, 幅, そしてバックグラウンドの強度に対応します。

[5.09489317e+03 7.70042192e+02 1.00241198e+01 8.11522007e+03
 7.75039390e+02 2.95737145e+00 1.84594901e+02]

#もっとピーク数が多い場合

例えば、次のようにもっとピーク数が多い場合を考えます。

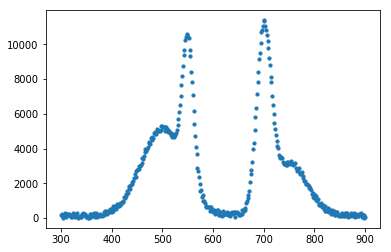
(なんだか不自然なデータですがご容赦ください)

この場合も、初期値設定の部分を少し書き換えるだけで対処できます。

guess = []
guess.append([4500, 490, 10])
guess.append([7500, 540, 10])

#ここから
guess.append([8000, 720, 10])
guess.append([2000, 740, 10])
#ここまでを書き加えるだけ！！！

background = 5

guess_total = []
for i in guess:
    guess_total.extend(i)
guess_total.append(background)

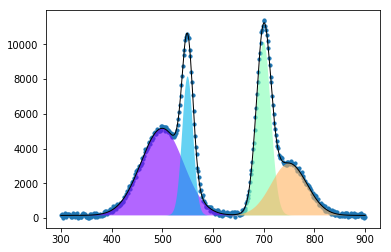
この部分を書き換えるだけで、他の部分に手を加える必要はありません。
最終的にフィッティングした結果を可視化すると以下のようになります。

#まとめ
私用でピークフィッティングをPythonで行う必要があったので、忘れないようにまとめておきました。
まあだいたいの人は実験機器に据え付けの解析ソフトでやってしまうと思います。実際そっちの方が楽で、正確です。

ただ、Pythonでもできるということを知っておくと、意外と役立つときがきます。

それでは！