はじめに
非常に大きくて明るい流れ星は、まるで火の玉のように見えるため、火球(Bolide)と呼ばれます。
火球はまれに音を伴って流れることが知られています。
しかし、火球の高度は100~200 km程度1であり、音が聞こえるまでは少なくとも5分以上はかかるはずです。そのため、この音の原因は火球の発する電磁波であると考えられており、”電磁波音(Electrophonic sound)”と呼ばれています。
音の発生メカニズムとして様々なモデルが考案されていますが、いまだ統一的な説明はないようです2。そもそも火球自体が珍しい上、目撃者のうち10%ぐらいしか音を感じない3という現象なので、科学的な検証が非常に難しいという問題があります。
しかし最近、ツイッター上でこの音を観測した人がいらっしゃいました。
しかも動画付き。
この火球では、流星が光ると同時に音が鳴る電磁波音も捉えることができました。どうして同時に音が鳴るか、詳しい理由はまだわかっていません。 pic.twitter.com/nJeSOr8h3h
— 藤井大地 (@dfuji1) November 14, 2019
というわけで、この動画の画像と音声を解析してみたいと思います。
プログラミング言語にはPythonを用います。
動画解析
動画解析にはOpenCVを使います。
まずは適当な方法でTwitterから動画をダウンロードします。
今回はmp4形式でダウンロードしました。
インポート
import cv2
import numpy as np
import matplotlib.pyplot as plt
動画の読み込み
まずは、動画ファイルを読み込んでフレームレートを見ます。
cap = cv2.VideoCapture('movie.mp4') #ファイル名を入力
framerate = cap.get(cv2.CAP_PROP_FPS) #フレームレート
print(framerate)
>> 29.97002997002997
よくある29.97 fpsですね。
では、1フレームずつ画像をグレースケールで読み込みます。
print(framerate)
images = []
while(cap.isOpened()):
ret, frame = cap.read()
try:
gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
except:
break
images.append(gray)
cap.release()
120フレーム目、だいたい t = 4 s の時点でのスナップショットを表示してみます。
plt.imshow(images[120])
plt.gray()
ちょうど火球が光ってるあたりですね。
では画像解析をしていきましょう。
画像解析
画像解析といっても、正式な計測方法は知らないので、単純に2値化して面積を計る方法で行きます。
とりあえず火球の大きさが分かればいいので大丈夫でしょう。
まずは火球だけが画像に写るようにトリミングします。
images_trim = [i[0:250,130:290] for i in images]
plt.imshow(images_trim[120])
トリミングした画像に二値化を掛けます。閾値は適当に設定しましょう。
__,th = cv2.threshold(images_trim[120],245,255,cv2.THRESH_BINARY)
plt.imshow(th)
二値化後の画像は上のような感じになります。この画像の中で白色の部分の面積を求めます。
では、すべての画像に同様の処理を行いましょう。
ついでに、元画像と2値化画像を重ね合わせた画像も作りました。
areas = [] #火球の面積
for n,i in enumerate(images_trim):
#火球面積の計測
__,th = cv2.threshold(i,245,255,cv2.THRESH_BINARY)
idx = np.where(th == 255)
areas.append(idx[0].shape[0])
#合成画像の作成
th = cv2.cvtColor(th, cv2.COLOR_GRAY2RGB)
th[idx] = [0,0,255]
img = cv2.cvtColor(i,cv2.COLOR_GRAY2RGB)
blended = cv2.addWeighted(img,0.7,th,0.3,1)
#合成画像の保存
cv2.imwrite('./bolides/'+str(n)+'.png',blended)
areas = np.array(areas)
合成画像をまとめてGif動画にするとこんな感じ。
二値化で得られた火球の領域を赤色で重ね合わせています。
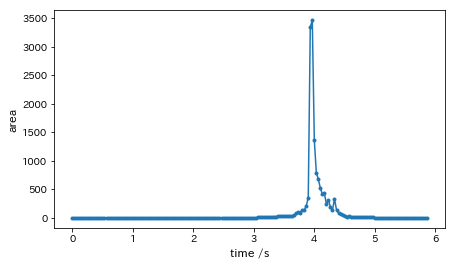
では、この火球面積の時間変化をプロットします。
xrange= np.arange(0,len(areas)/framerate,1/framerate)
fig = plt.figure(figsize=(7,4))
plt.plot(xrange,areas,'o-',ms=3)
plt.xlabel('time /s',fontsize=12)
plt.ylabel('area',fontsize=12)
だいたい3.8秒ぐらいで立ち上がり、4秒あたりで極大に至っていることがわかります。
動画解析はこれくらいでいいでしょう。
音声解析
音声の読み込みにはpydubを、解析にlibrosaを使います。
便利なライブラリが多くて助かりますね。
インポート
import librosa
import librosa.display
from pydub import AudioSegment
音声読み込み
以下のコードで動画ファイルから音声データを読み込み、numpyのarray形式に変換します。
# 動画からの音声の読み込み
sound = AudioSegment.from_file('movie.mp4')
data = np.array(sound.get_array_of_samples())
また、サンプルレート、総時間、チャンネル数は以下のように表示できます。
# サンプルレート, 総時間,
rate = sound.frame_rate
time = sound.duration_seconds
channel = sound.channels
print('rate: '+str(rate)+' Hz')
print('time: '+str(time)+' s')
print('channel: '+str(channel))
結果は以下のようになります。
- rate: 44100 Hz
- time: 5.921088435374149 s
- channel: 2
チャンネル数が2のステレオ音声なので、左右のデータを分ける必要があります。
pydubでは、ステレオ音声のarrayとしての出力は偶数番目と奇数番目の要素に分割されているので、以下のようにして別々に取り出します。
left = data[::2] #左の音声
right = data[1::2] #右の音声
今回の解析には左の音声を使います。とりあえずプロットしてみましょう。
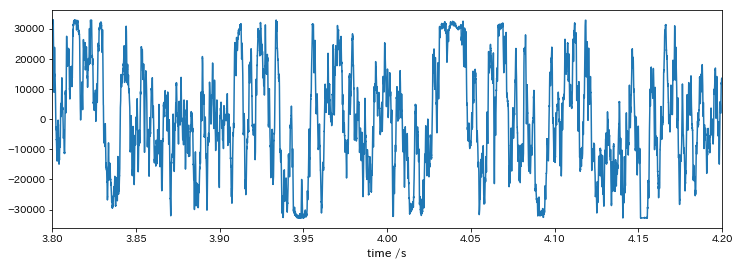
火球が極大に達する辺りの3.8s~4.2sのデータを表示します。
fig = plt.figure(figsize=(12,4))
plt.plot(np.linspace(0,left.shape[0]/rate-1,left.shape[0]),left)
plt.xlim(3.8,4.2)
plt.xlabel('time /s',fontsize=12)
ちゃんとデータが取れていることが分かりますが、何が何だかわかんないですね。
頭の中でフーリエ変換できる人ならあるいは・・・。
まあ素直にスペクトログラムを書きましょう。
音声の周波数解析-スペクトログラム
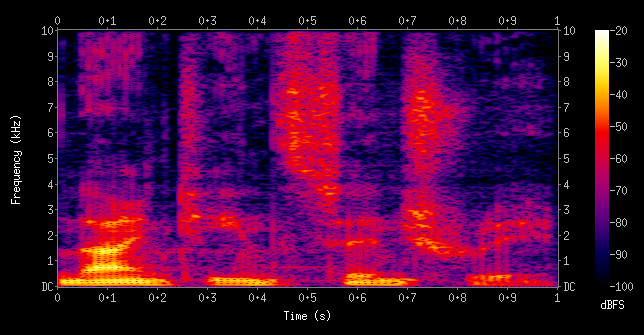
(From wikimedia commons, Aquegg [Public domain])
スペクトログラム(英: Spectrogram)とは、複合信号を窓関数に通して、周波数スペクトルを計算した結果を指す。3次元のグラフ(時間、周波数、信号成分の強さ)で表される。(wikipedia)
刑事ドラマの声紋分析とかでたまに出てくるあれです。横軸が実時間(s)、縦軸が音の周波数(Hz)、色が音の強度(dB)で表されるグラフです。
実際に、火球の電磁波音の研究としてスペクトログラムを解析されている方もいます4。
周波数ごとの強度を求めるのはもちろんフーリエ変換ですが、音声信号の処理では、狭い領域でフーリエ変換を行ったものを重ねあわせる短時間フーリエ変換(STFT: Short-time fourier transform)が使われます。
このような音声解析をPythonで行うには、librosaというライブラリが便利です。スペクトログラムの作成には以下のサイトを参考にしました。
Pythonで音声解析 – 音声データの周波数特性を調べる方法
スペクトログラムの作成
以下のコードで短時間フーリエ変換を行います。
フレーム長(フーリエ変換をする領域)とフレームシフト長(フレームごとの間隔)はいい感じに変えましょう。
# 音声ファイルのデータを-1~1の範囲で正規化
left = left / np.max(left)
# フレーム長
fft_size = 1024
# フレームシフト長
hop_length = int(fft_size / 4)
# 短時間フーリエ変換実行
amplitude = np.abs(librosa.core.stft(left, n_fft=fft_size, hop_length=hop_length))
# 振幅をデシベル単位に変換
log_power = librosa.core.amplitude_to_db(amplitude)
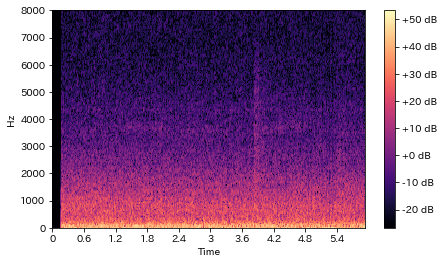
結果をグラフで表示してみましょう。
fig = plt.figure(figsize=(7,4))
librosa.display.specshow(log_power, sr=rate, hop_length=hop_length,
x_axis='time', y_axis='hz', cmap='magma')
plt.colorbar(format='%+2.0f dB')
plt.ylim(0,8000)
ノイズが多くてはっきりしないですが、4秒あたりで変化があるように見えますね。
とりあえずはこれで良しとします。
動画と音声データの比較
せっかく動画と音声が一緒にあるのだから、2つを比較してみたいですね。
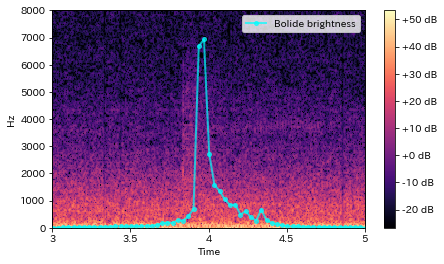
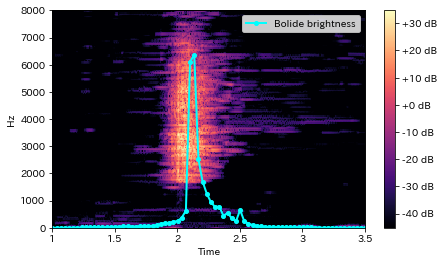
先ほどの画像解析の結果(火球のサイズ変化)を、スペクトログラム上にプロットしてみます。
fig,ax1 = plt.subplots()
librosa.display.specshow(log_power, sr=rate, hop_length=hop_length,
x_axis='time', y_axis='hz', cmap='magma')
plt.colorbar(format='%+2.0f dB')
ax1.set_ylim(0,8000)
ax2 = ax1.twinx()
ax2.plot(xrange,np.array(areas),c='cyan',lw=2,marker='o',ms=4,label='Bolide brightness',alpha=0.7)
ax2.set_ylim(0,4000)
ax2.tick_params(labelright=False)
ax2.tick_params(right=False)
plt.xlim(3,5)
plt.legend()
plt.show()
確かに、火球の立ち上がりと同時に高い音が鳴っていることが分かります。
また、火球が最大となる時点よりも前から音は鳴り始めているようです。
音声のノイズ除去
なんか音声がはっきりしないし、デノイズできたらいいなあ、と思っていたら、すでにツイッター上に上げている人がいました。
ノイズを除去してみました。 pic.twitter.com/imr8yJ9HN6
— ナッパ教信徒 (@nappasan) November 18, 2019
す、すばらしい・・・!
ということでこのデノイズ済みの動画を解析した結果がこちらです。
スペクトログラムがものすごい明確になりました。
やはり、電磁波音は火球の極大よりも少しだけ早く聞こえているみたいです。
ふしぎですね。
最後に
実はこの解析、1月ぐらい前に動画+音声処理の練習としてやったものです。
スペクトログラム作ってみた。4秒付近に高い音のピークがあって、火球が最大となるタイミングと一致している。ふしぎだなあ。 https://t.co/Zpgc6r0pqd pic.twitter.com/Q73ZVNGYGE
— konkon (@konkon28983820) November 21, 2019
大した内容でもないし結果を1つ2つツイートして満足していたんですが、天文学 Advent Calendar 2019なんて面白いものができていたので、ここで出さなきゃいつ出すの! と思い、改めてまとめました。
これって天文学か・・・? 地球物理学とか惑星科学では? と一瞬思いましたが、もう完成したからまあいいや。
拙い解析ですが、何か皆さんのお役に立てるようであれば幸いです。