Feedback Control of Real-Time Display Advertising
WSDM 2016 勉強会 での発表資料です。次の論文の解説になります。
Feedback Control of Real-Time Display Advertising by Weinan Zhang, Yifei Rong, Jun Wang, Tianchi Zhu, Xiaofan Wang
問題設定
背景
- インターネット広告 > ディスプレイ広告 > RTB (Real-Time Bidding) の世界の話
- 「ディスプレイ広告」は、ここではいわゆる「バナー広告」の類だと思って貰えれば OK
- バナー広告以外には「検索連動型広告」(Google AdWords など) があるが、こちらはこの論文のスコープ外
- RTB における登場人物 (組織・システム)
- Publisher
- Web メディアなどの「広告枠」を持っている人
-
Advertiser
- 広告主
- SSP (supply-side platform)
- 「広告枠」を提供する側のプレイヤーが利用するプラットフォーム
- アドオークションを開催する人 (システム)
-
★ DSP (demand-side platform)
- 広告主 (広告代理店) が利用するプラットフォーム
- アドオークションに参加して入札する人 (システム)
- Publisher
動機
- Advertiser は広告枠を購入し、その広告枠に自分の広告を表示したい
- 広告を表示して (インプレッションを獲得して)、クリックやコンバージョンを獲得したい
- Advertiser は KPI を持っている
- CPM (cost per mille): 1,000 回のインプレッションをするのに要した費用
- AWR (auction winning ratio): アドオークションでの勝率
- eCPC (effective cost per click): 1 クリックを獲得するのに要した費用
- CTR (click-through rate): クリック率
- Advertiser は、これらの KPI を最適化 (※) したい
- ※ 最適化、というよりも、目標数値に収束させる、というのが正しいかも
- eCPC を低く抑えたり、CTR を高めたりしたい
- RTB においては、これらの KPI が時間推移によって大きく上下に変動しうる
- 上下に変動してしまうと、KPI を最適化するのも一苦労となる
論文が提案する解決法
- KPI をその目標数値に収束させる問題に対して、「フィードバック制御」を取り入れる
- 最適化対象の KPI は、具体的には:
- 獲得を目的とした広告であれば、eCPC となる
- ブランディング・認知目的の広告であれば、AWR となる
- これらの KPI の制御に使える変数は、 bid price (オークションにおける入札額) となる
- bid price を、フィードバック制御の出力値とする
- フィードバック制御の方法:
- PID: proportional-integral-derivative controller
- WL: Waterlevel-based controller
- さらには、入札最適化 (bid optimization) = マルチチャネルでの広告出稿の最適化 (※) にも、このフィードバック制御を導入してみる
- ※ コストパフォーマンスの悪いチャネルへの広告出稿を控え (割り当て予算を減らし)、コストパフォーマンスの高いチャネルにその予算を寄せる
フィードバック制御を組み込んだ DSP bidding agent
概要
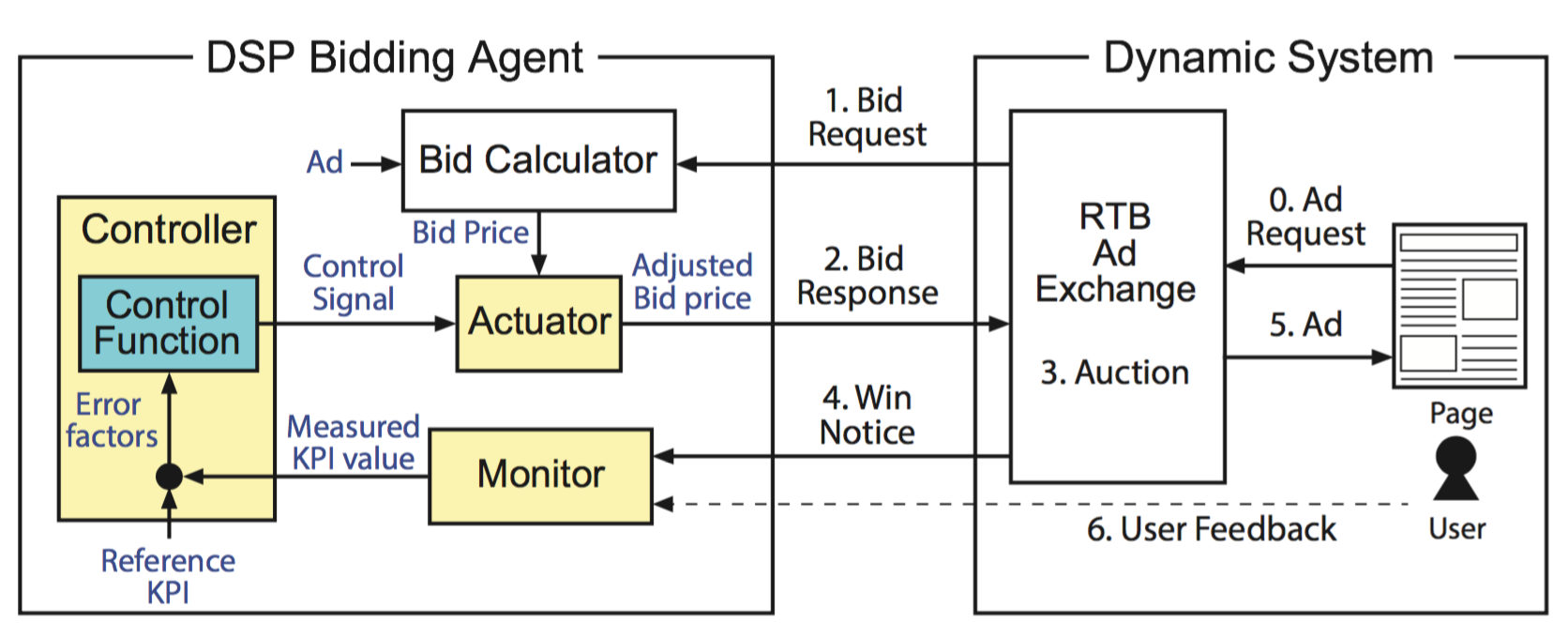
処理の流れ
- 入札リクエストを受け付ける
- 入札額を算出する (Bid Calculator)
- 入札単価状況や予測された CTR (or Conversion rate) を基に計算する
- 詳しくは「入札戦略」で説明する
- 入札額を調整する (Actuator)
- PID or WL を利用する
- こちらも「フィードバック制御」で詳しく説明する
- 入札レスポンスを返却する
- Win notice を受け取る (オークションに勝利した場合のみ)
- Controller にフィードバックする
- ユーザの行動 (クリック or コンバージョン) を受け取る
- こちらも Controller にフィードバックする
入札戦略
- よく使われている入札戦略が存在するらしい
- 予測された CTR $\theta_t$ と、平均的な CTR $\theta_0$ 、ベースの入札額をもとに入札単価状況によって調整された入札額 $b_0$ より、次の式で入札額 $b(t)$ を決定する
b(t) = b_0 \frac{\theta_t}{\theta_0} \tag{1}
- 入札単価状況を求める手法は次の論文に書かれているぽい
 フィードバック制御
フィードバック制御
ここがこの論文の肝です。
- $(1)$ の入札戦略によって算出された入札額を、Actuator によって調整して最終的な入札額 $b_a(t)$ とする
b_a(t) = b(t)\exp\{\phi(t)\} \tag{2}
- $\phi(t)$ は PID or WL で計算される値である
- ちなみに、筆者らは $b_a(t) = b(t)(1 + \phi(t))$ などの線形なモデルも試してみたとのことで、こちらは性能が悪かった模様
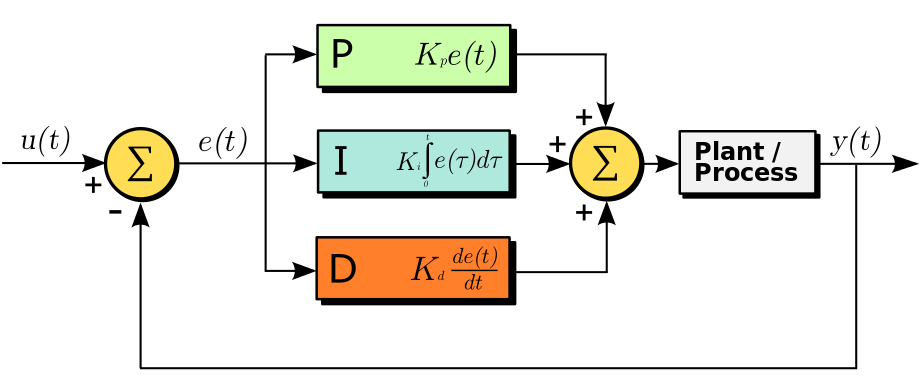
PID Controller
- PID によってフィードバック制御を実現する
- 以下 Wikipedia からの引用
PID制御は、制御工学におけるフィードバック制御の一種であり、入力値の制御を出力値と目標値との偏差、その積分、および微分の3つの要素によって行う方法のことである。
- 具体的には、次の式で計算される
e(t_k) = x_r - x(t_k) \tag{3}
\phi(t_{k+1}) \leftarrow \lambda_P e(t_k) + \lambda_I \sum_{j=1}^k e(t_j) \Delta t_j + \lambda_D \frac{\Delta e(t_k)}{\Delta t_k} \tag{4}
- それぞれの意味は次のとおり
- $(3)$ 式は、KPI の目標値 $x_r$ と、時刻 $t_k$ における KPI の実績値 $x(t_k)$ との差を表す
- $\Delta t_j = t_j - t_{j-1}$ : 時刻 $t_j$ と $t_{j-1}$ の間の時間差を表す
- $\Delta e(t_k) = e(t_k) - e(t_{k-1})$ : 時刻 $t_k$ と $t_{k_1}$ のそれぞれの実績値同士の差を表す
- $(4)$ 式は PID 制御の伝達関数に相当する
- $\lambda_P, \lambda_I, \lambda_D$ はそれぞれ、比例ゲイン、積分ゲイン、微分ゲインを表すパラメータ
Waterlevel-based Controller
- こちらは PID 制御よりもシンプル
\phi(t_{k+1}) \leftarrow \phi(t_k) + \gamma (x_r - x(t_k)) \tag{5}
- $\gamma$ はステップサイズパラメータを表す
オフラインでの実験・評価
データセット
-
iPinYou DSP のデータセットを利用
- 10 日分
- 9 キャンペーン
- 約 6475 万の入札ログ
- オークションでの勝利に必要な最低入札価格が含まれる
- 約 1950 万のインプレッションログ
- 約 1 万 4000 のクリックログ
- 入札戦略の $(1)$ 式で利用する CTR の予測には、ロジスティック回帰を利用する
評価方法
- iPinYou のデータセットを用いて、eCPC と AWR のそれぞれの KPI について目標値を設定し、実績値をそれに収束させることを試みる
- 論文には明示されていない気がするけど eCPC と AWR はそれぞれ別に分けて実験をしているはず…
- 手順は以下のとおり
- 入札ログのレコードを DSP bidding agent に与える
- DSP bidding agent は入札価格を算出する
- 算出された入札価格が、オークションでの勝利に必要な最低入札価格を上回っていれば、オークションに勝利したものとして取り扱う
- オークションに勝利した場合
- インプレッションログを DSP bidding agent に与える
- クリックログが存在するなら、それも与える
- $\phi(t)$ の更新は 2 時間ごとに行う
- この更新を 1 ラウンドとする
評価に使う指標値
収束速度に関わる指標値
-
Rise time
- 実績値が、エラーバンド (最適化対象の KPI の目標値 ± 10% 以内) に最初に到達するまでに要した時間
-
Settling time
- 実績値が、エラーバンド内に定着するまでに要した時間
精度に関わる指標値
-
Overshoot
- 実績値が KPI 目標値を超えてしまった割合 (%)
-
RMSE-SS
- 実績値がエラーバンド内に定着した以降における、目標値と実績値の RMSE
安定性に関わる指標値
-
SD-SS
- 実績値がエラーバンド内に定着した以降における、実績値の標準偏差
実験結果
基本的な収束性能
-
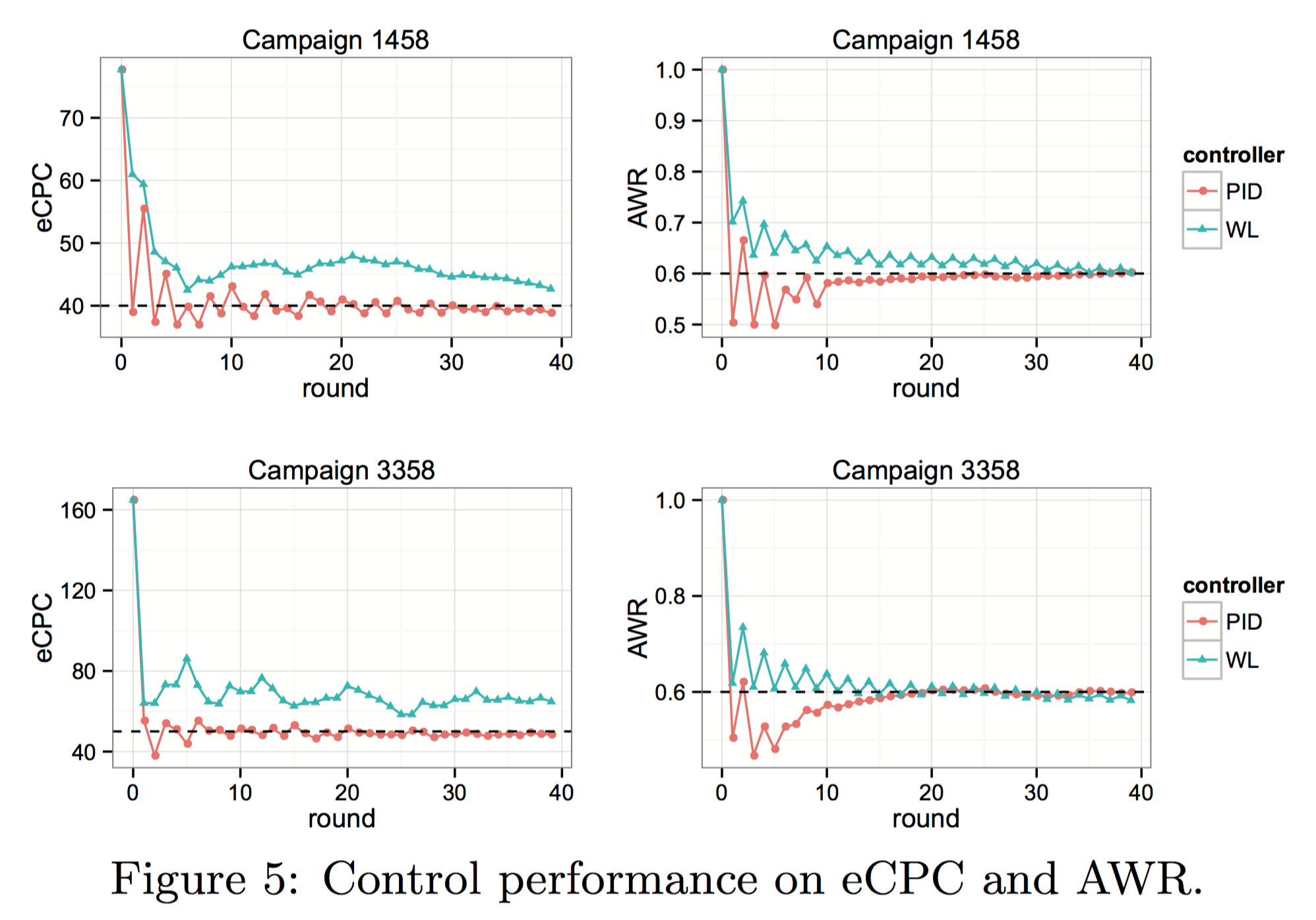
Table 1, 2 と、 Fig. 5 を参照
-
PID は いずれのキャンペーンにおいても、実績値を目標値に収束させることができた
-
一方で WL は、収束に失敗したキャンペーンが存在している
- 特に eCPC の収束がうまくいっていない
-
精度の良さは、PID > WL となる
-
Overshoot は WL の方が少ない
-
(PID, WL は関係ないが) CTR 予測の精度が高いとエラーバンド内に定着するまでの時間が短くなる
-
総じて言えることは、PID の方が収束性能がいいね、ということ
収束の難易度を変化させた状況での性能
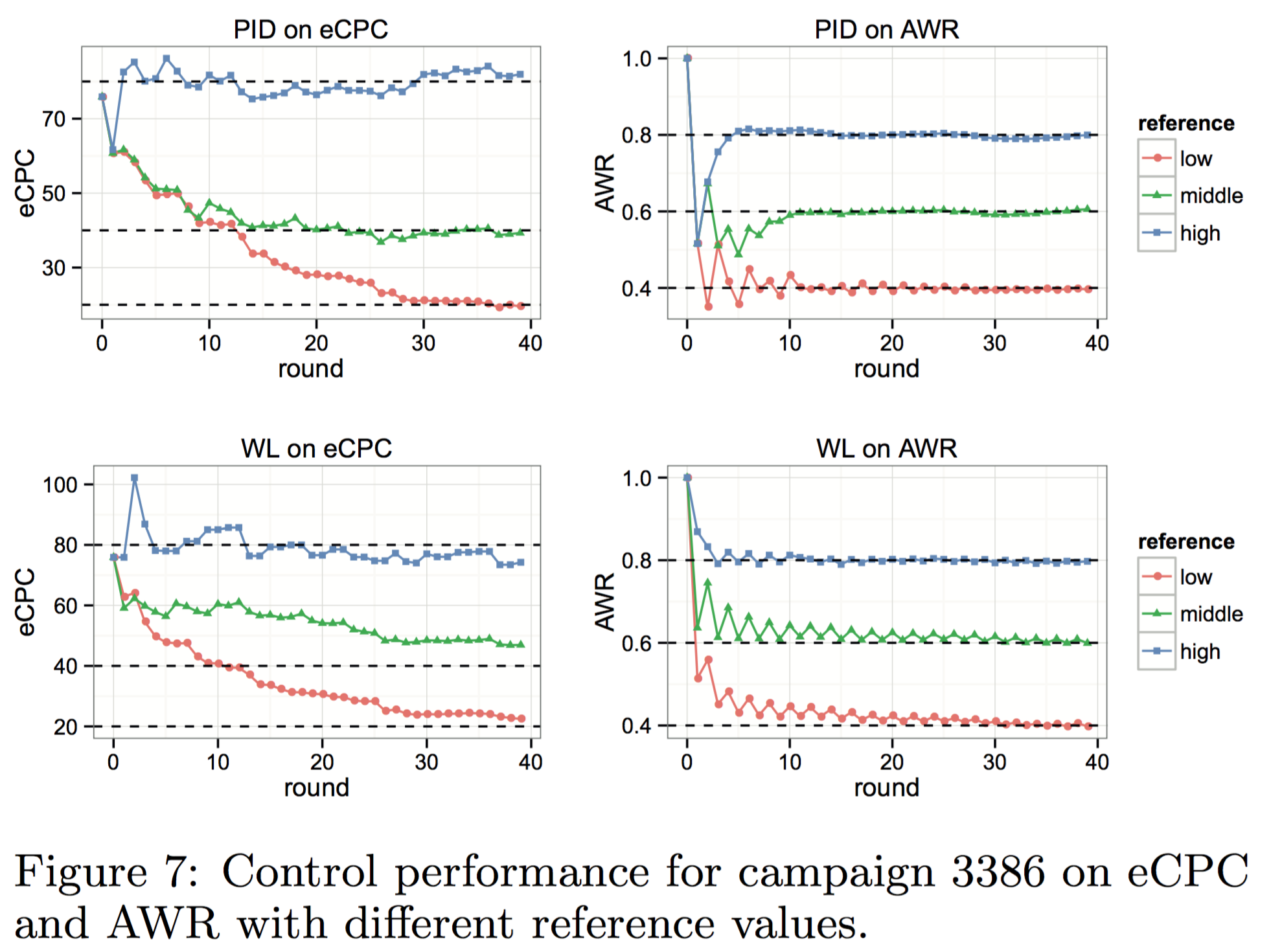
- KPI の目標値を過度に高く (簡単に) or 低く (難しく) して実験してみる
- Fig. 6, 7 を参照
- PID も WL も、過度に難しい (低い) 目標値を設定すると、収束しなかったり変動が激しくなるリスクが生じる
パラメータチューニング
- 主に $\lambda_P, \lambda_I, \lambda_D$ のパラメータをチューニングする、という話
パラメータ探索
- $\lambda_D$
- このパラメータは制御性能を大きく変える効果はない
- $1 \times 10^{-5}$ ぐらいの小さな値を設定しておく (チューニングはしない)
- overshoot の発生を減らし、また収束するまでの時間が僅かに短くなる
- $\lambda_P, \lambda_I$
- これらのパラメータチューニングは本来ならグリッドサーチで実現するべき
- でも論文では、それぞれ一方のパラメータを固定し、もう一方のパラメータだけを変化させる方法で、片方ずつチューニングする方法を紹介している
- ステップサイズを指数的に小さくしていき、局所最適なパラメータを見つける
- 確かに計算量的には小さくなるが、それでいいのか…
phi(t) の上限・下限設定
- $\phi(t)$ の値に対して上限値と下限値を設けた方が制御しやすくなる
- 下限値を設けることで、オークションに勝てなくなる自体を避けることができる
- 上限値を設けることで、過度に高い入札額の提示を避けることができる
- 例えば今回の実験は $[-2, 5]$ の範囲にする、など
オンラインでのパラメータ更新
- オンラインのプロダクション環境などでは、インプレッションやクリックなどのフィードバックがリアルタイムで到着する
- パラメータの更新を、オンラインで実施しようと思えばできる
- 1 回のパラメータ探索は 10 分程度で済む
- 10 ラウンドごとにパラメータを更新してみたときに、どのようにパフォーマンスが変化するか?
-
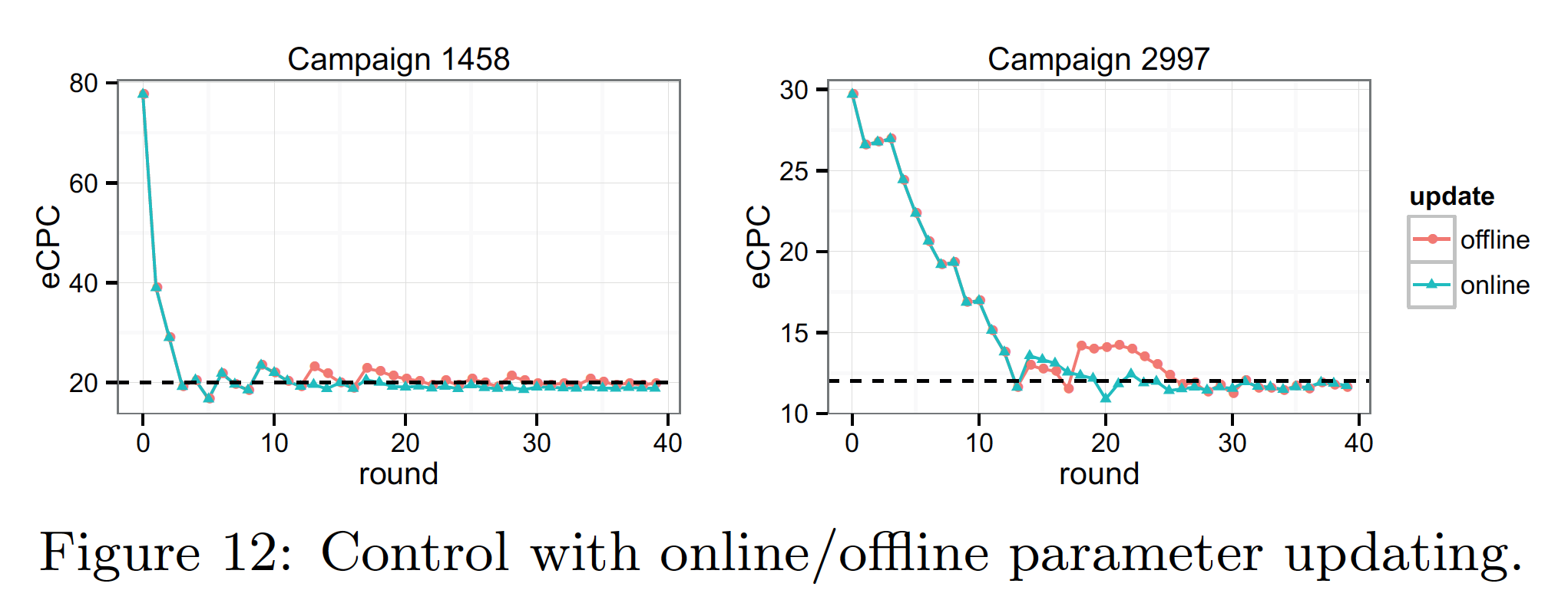
- 実際に、収束性能がよくなっているのが分かる
- Settling time は短くなり、 Overshoot も少なくなるとのこと
実際のオンライン環境下での実験
- 中国における運用型モバイル広告の DSP、 BigTree に組み込んで実験してみた
-
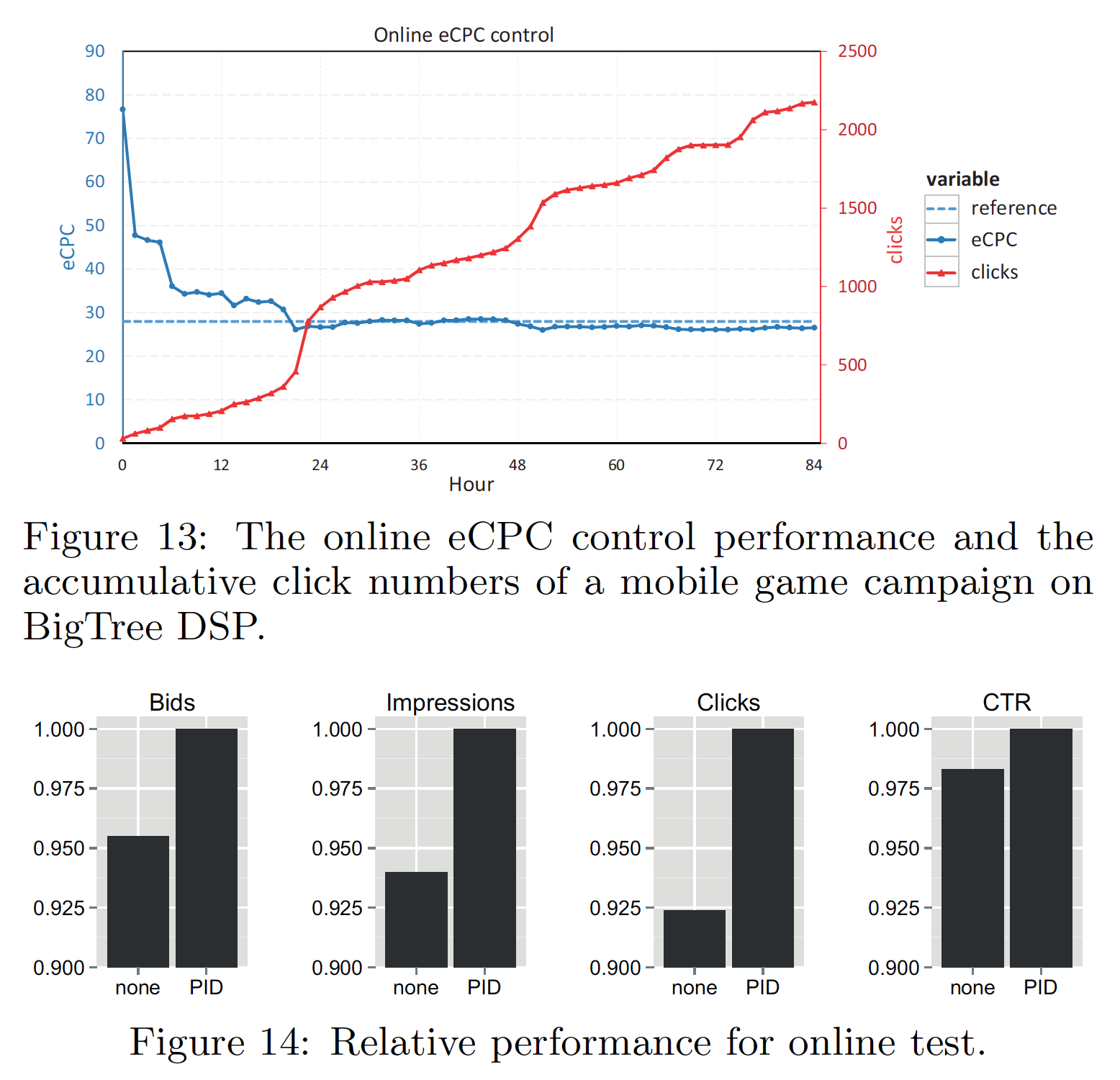
- 上図 (Fig. 13)
- フィードバック制御によって、確かに KPI の目標値 (eCPC) に収束している!
- クリックもちゃんと獲得できている
- 下図 (Fig. 14)
- フィードバック制御がない場合と比較して、bids (オークションでの勝率?)、インプレッション数、クリック数、CTR が良くなっている
- KPI の目標値 (eCPC) は低めに設定した
- フィードバック制御がない方の eCPC については言及されていない…
まとめ
- DSP (demand-side platform) における、広告パフォーマンスを測る KPI を最適化したい
- フィードバック制御の考えを導入して、KPI の最適化を試してみた
- PID と Waterlevel-based の二つのフィードバック制御手法を比較してみた
- オフラインでの実験の結果、PID の方がよかった
- オンラインでも実験し、実際に KPI が最適化できることを確認できた