計算量オーダーのグラフ作った

はじめに

計算量オーダーの大きさの違いがわからなかったので、グラフを作ってみました。

$O(\log{n})　O(\sqrt{n})　O(n)　O(n\log{n})　O(n\sqrt{n})　O(n^2)　O(n^3)　O(n^4)　O(2^\frac{n}{2})　O(2^n)　O(n!)$

上のの11個についてグラフにしてあります。
※計算量の小さい順に並べてあります。

対数目盛にしたほうが良いというご指摘をいただきましたが、本稿では直感的に分かりやすいよう、あえて線形目盛（普通の目盛）を使用しています。

全部含めたグラフ

横軸に$n$を取り、縦軸に$O(k)$を取っています。
横軸は続く3つのグラフで1メモリが10になっています。
$O(n\sqrt{n})$より大きくなるものは密集しすぎてわからないので、①のグラフまで見送ります。

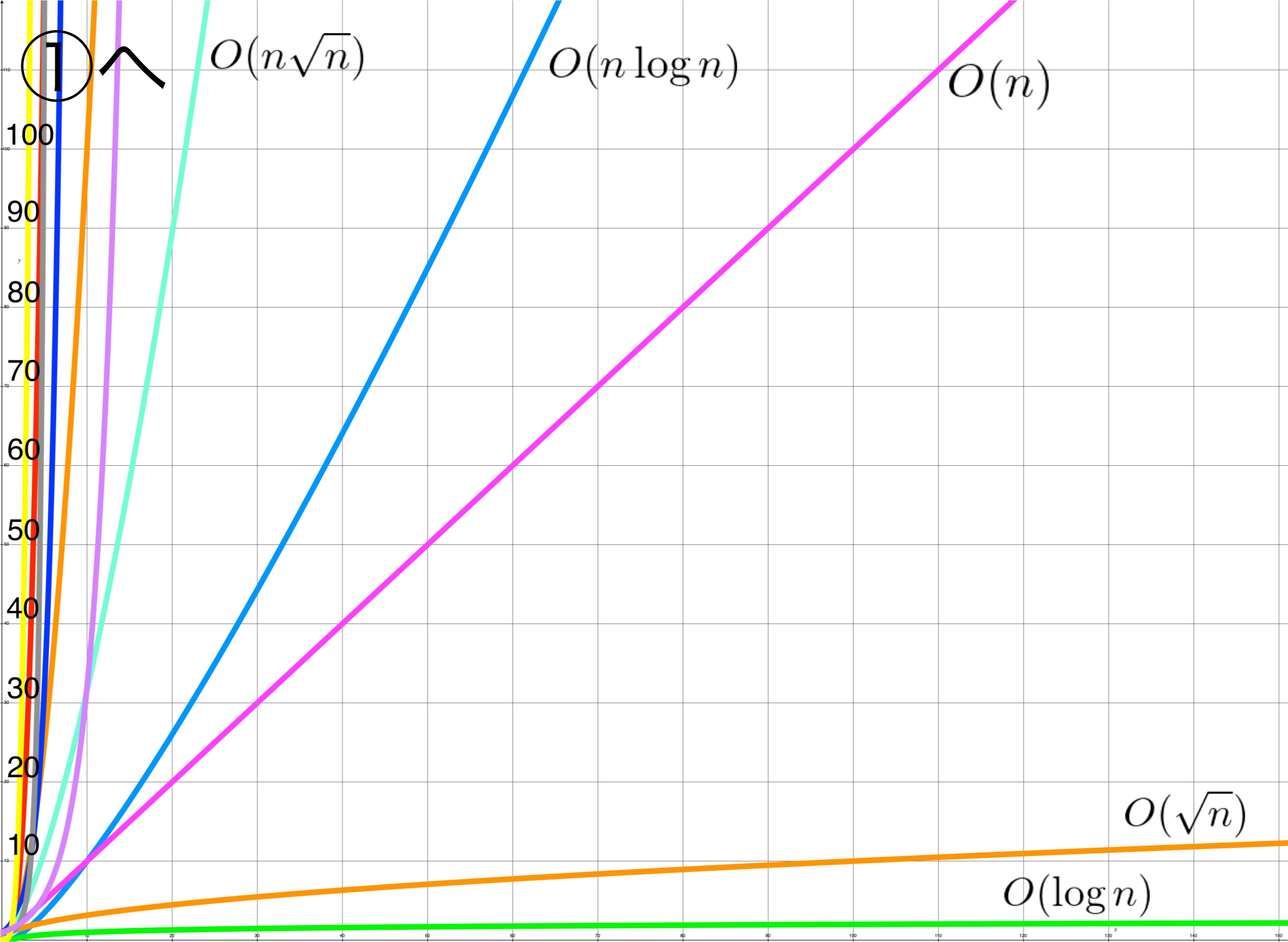
圧倒的$O(\log{n})$の強さ。$O(\sqrt{n})$もいい戦いですね。
$O(n\log{n})$がいまいちピンと来なかったのですが、これを見ると$O(n)$より少し計算量が大きくなっている程度だということがわかります。

①続き

縦軸のみ100倍くらい縮小して見てみます。

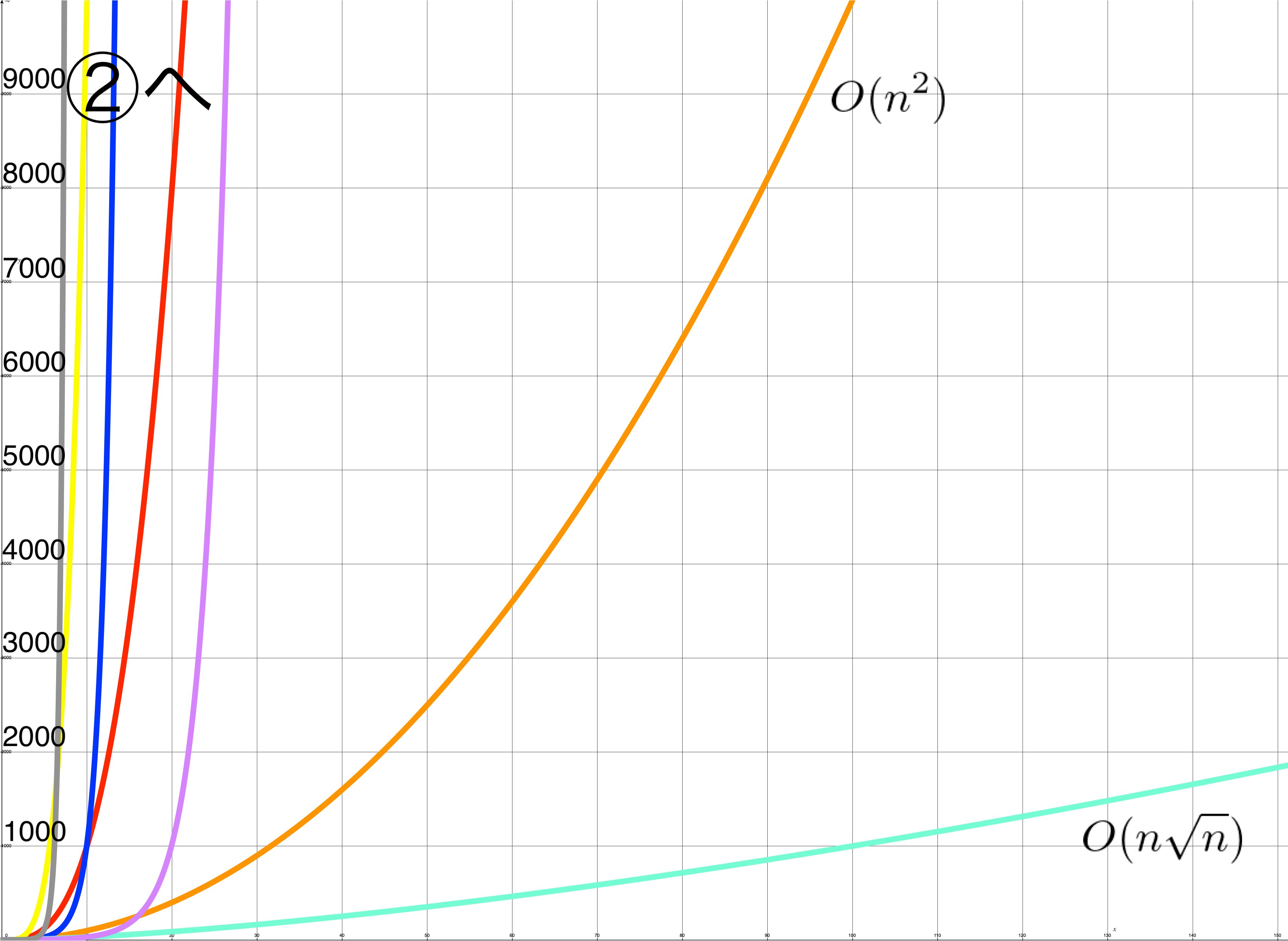
$O(n\sqrt{n})$と$O(n^2)$が見えてきました。
この２つは計算量的にもまあまあ使えるゾーンですが、その他のものは天に向かって伸びていっております。
おそろしや。

②続き

更に縦軸を$10^4$倍くらい縮小しました。
このグラフの天井は$10^8$となっているので、これを超えると厳しくなってくる計算量です。

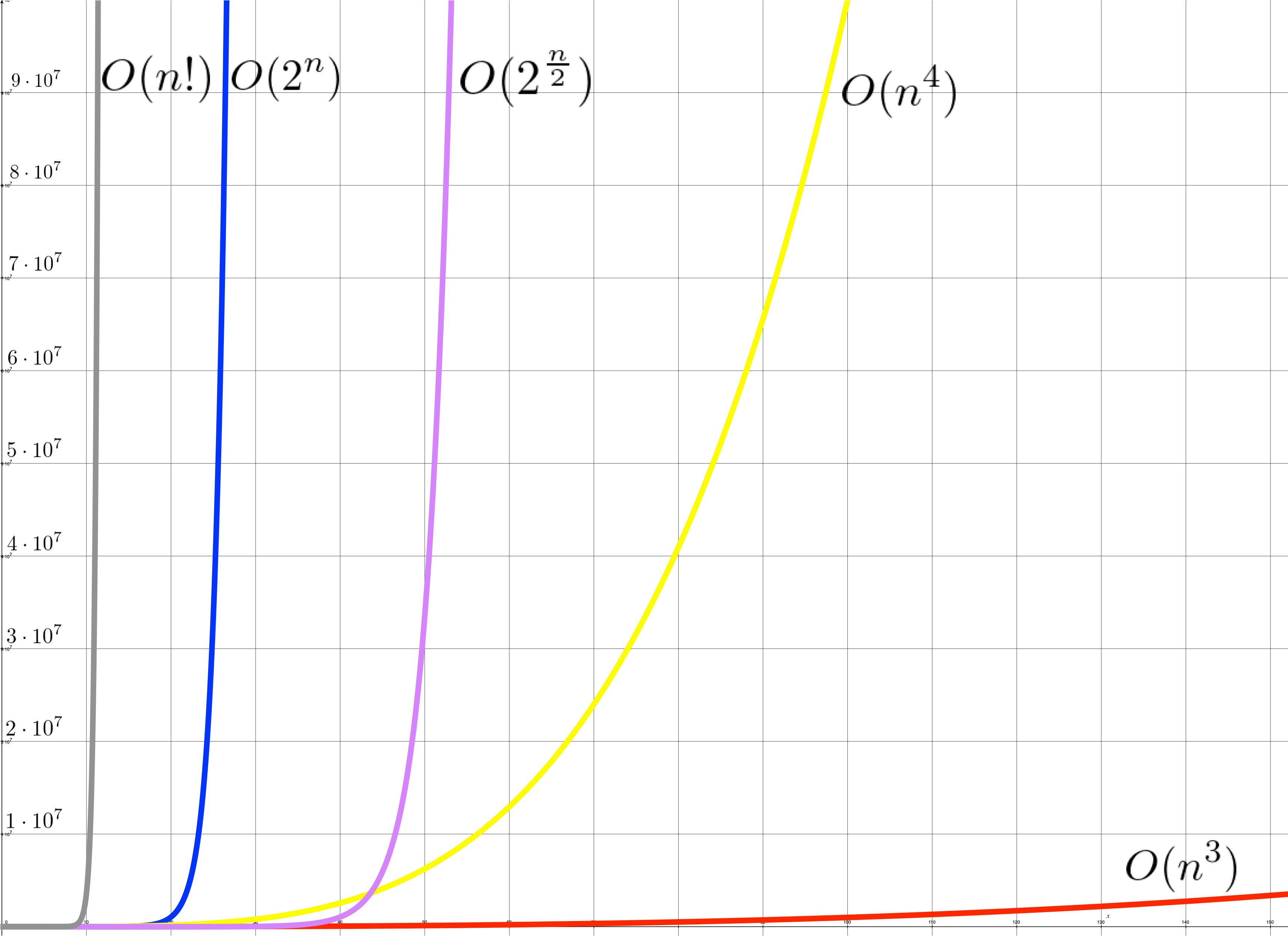
横軸が1メモリ10になっているのですが、$O(n^3)$以外は $n=100$ で力尽きてしまいます。
一方、$O(n^3)$を見ると、このグラフ上ではものすごく計算量が少ないように見えますが、$n$が増えるとぐんぐん成長していきます。
これらの計算量のアルゴリズムを使うときは、$n$と相談しながら使うのが良いのではないでしょうか。

教訓

• アルゴリズムを考えるときは$n$と相談しよう
• 計算量を考えよう

参考

• 計算量オーダーの求め方を総整理！ 〜 どこから log が出て来るか 〜
  • それぞれの$O(k)$についての限界などが詳しく載っています
• [初心者向け] プログラムの計算量を求める方法
  • 計算量という概念を教えて頂いた素晴らしい記事