はじめに
Pythonでフーリエ変換という記事をみた。
数学は全くわからないのだが、Ruby向けのグラフ描出ツールGR.rbを作っている人間としてはRubyで同じことができるか気になってしまう。
そこで最初のガウス分布のフーリエ変換を見様見真似で真似してみた。数学は全くわからないのだが。
グラフ描出にはGR.rbを使う。
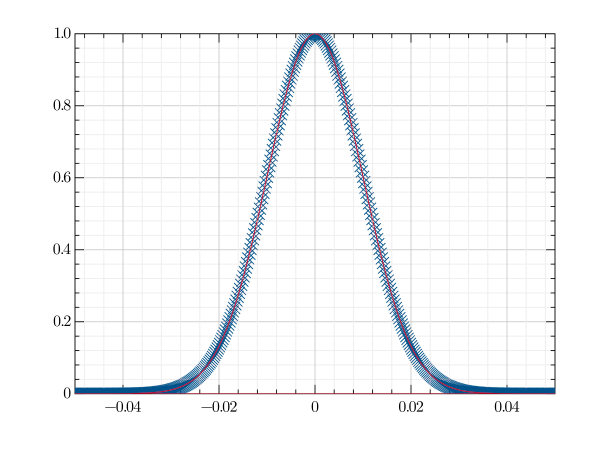
ガウス分布のフーリエ変換
require 'numo/narray'
require 'numo/pocketfft'
require 'gr/plot'
N = 4096 # サンプル数
s = N / 256 # 標準偏差
pi = Math::PI
y = Array.new(N) do |i|
x = i - N / 2
Math.exp(-x**2 / (2.0 * s**2)) / (Math.sqrt(2 * pi) * s)
end
freq = Numo::DFloat.linspace(0,1,N+1)
freq[N/2..-1].inplace - 1.0
freq = freq[0..-2]
theory = freq.map { |k| Math.exp(-(2 * pi * k)**2 * s**2 / 2.0) }
x = freq
y = Numo::Pocketfft.fft(Numo::NArray.cast(y)).abs
GR.plot([x, y, 'bx'], [x, theory, 'r'], xlim: [-0.05, 0.05])
GR.savefig('gaussian.png')
FFTを実行してくれそうなライブラリはRubyにも結構いろいろある。numo-fftwとか、numo-ffteとか。
今回はRumaleの作者である@yoshokuさんが作成している新しいnumo-pocketfftを利用した。
途中でつまずいたのは、fftfreq 関数がないことである。
最初はPyCallを使ってPythonを呼んでいたが
require 'pycall/import'
include PyCall::Import
pyimport :numpy, as: :np
freq = np.fft.fftfreq(N) # Python配列
freq = freq.tolist.to_a # Rubyの配列に変換
結局上のサンプルでは、NArrayの機能を使って自分で作るようにした。
NArrayの inplaceは特に深い意味はなくて n.inplace + b は n+=b と同じです。
数学はわからないですが、Rubyでも似たようなグラフが描けていると思う。
おまけ: uplotの紹介
現在、標準入力からUnicodePlotを使ってグラフを描出するuplotというコマンドラインツールを作成中である。
これを使うとこんなこともできる。(元のガウス分布のグラフ)
N = 4096 # サンプル数
s = N / 256 # 標準偏差
pi = Math::PI
N.times do |i|
x = i - N / 2
puts Math.exp(-x**2 / (2.0 * s**2)) / (Math.sqrt(2 * pi) * s)
end
ruby g.rb | uplot line --xlim 1948..2148
完成したらQiitaに紹介記事を書きます。
追記
なぜかトレンドに上がってしまっているので慌てて他のものも追加。
時系列(指数減衰)
require 'numo/narray'
require 'numo/pocketfft'
require 'gr/plot'
N = 4096
h = 0.1
gamma = 0.2
v0 = 2.0
v = v0
f = []
x = []
N.times do |i|
v -= gamma * v * h
f << v
x << i
end
y = Numo::Pocketfft.fft(Numo::NArray.cast(f))
freq = Numo::DFloat.linspace(0, 1, N + 1) * 10
freq[N / 2..-1].inplace - 10.0
freq = freq[0..-2]
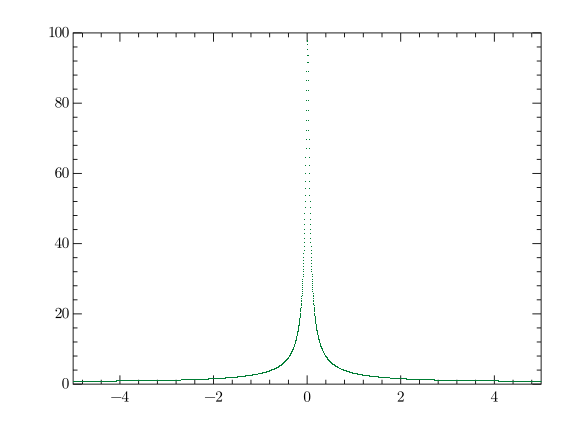
GR.plot(freq, y.abs, 'g.', grid: false)
GR.savefig('decay.png')
freq検算用
# require 'pycall/import'
# include PyCall::Import
# pyimport :numpy, as: :np
# freq2 = np.fft.fftfreq(N, d: 0.1) # Python配列
# freq2 = freq2.tolist.to_a # Rubyの配列に変換
# p freq2 == freq # true
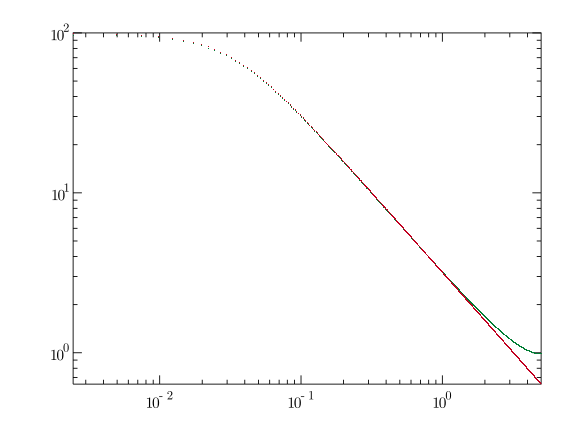
theory = freq.map { |w| v0 / Math.sqrt((w * 2 * Math::PI)**2 + gamma**2) / h }
GR.plot([freq, y.abs, 'g.'], [freq, theory, 'r.'],
grid: false, xlog: true, ylog: true)
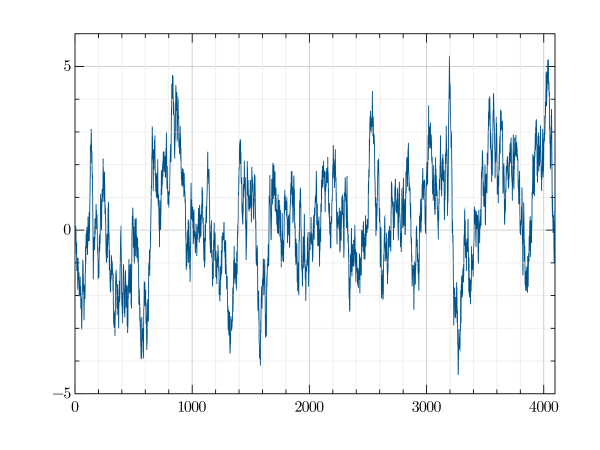
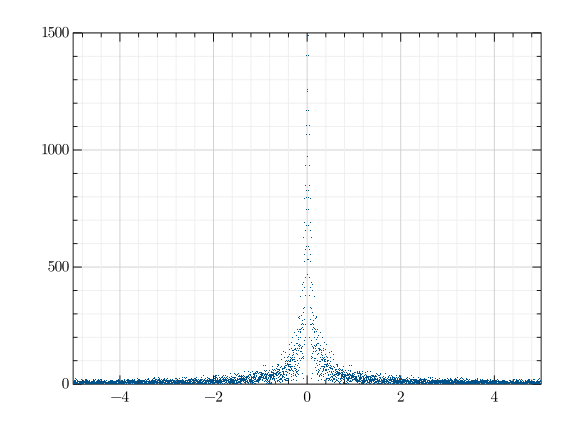
時系列(ランジュバン方程式)
require 'numo/narray'
require 'numo/pocketfft'
require 'gr/plot'
N = 4096
h = 0.1 # 時間刻み
gamma = 0.2 # 減衰係数
v0 = 0.0 # 初速
v = v0
x = []
f = []
N.times do |i|
v = v -gamma * v * h + Numo::DFloat.new(1).rand_norm(0, Math.sqrt(h))[0]
x << i
f << v
end
GR.plot(x,f, xlim: 0..4096)
fw = Numo::Pocketfft.fft(Numo::NArray.cast(f))
freq = Numo::DFloat.linspace(0, 1, N + 1) * 10
freq[N / 2..-1].inplace - 10.0
freq = freq[0..-2]
GR.plot(freq, fw.abs, '.')
theory = freq.map{|w| Math.sqrt(N*h)/Math.sqrt((2*Math::PI*w)**2 + gamma**2)/h}
GR.plot([freq, fw.abs, '.'], [freq, theory, 'r'],
size: [100, 75], xlog: true, ylog: true)
理論面はPythonの元記事を見てください。グラフはなんとなく正しそうだけど、理論面は私は全くわかってないので、一応確認してから使ってください。
この記事は以上です。