ポイント
- ゲストグラフ$G$をホストグラフ$H$に埋め込むグラフの埋め込み問題を等価なQUBOに変換する方法
- PyQUBOによるQUBOの生成
- GurobiによるQUBOの解を求める方法
- 埋め込みが成功したら,解探索を終了するGurobiのコールバック関数の設定法
- NetworkXを用いた無向グラフの描画
グラフの埋め込み問題
問題の入力は,ゲストグラフ$G=(V_G,E_G)$とホストグラフ$H=(V_H,E_H)$です.いずれも無向グラフで$V_G$と$V_H$が頂点集合,$E_G$と$E_H$が辺集合,つまり頂点の無順序対です.求めるのは$V_G$から$V_H$への埋め込み,つまり写像$f:V_G\rightarrow V_H$です.ゲストグラフの辺集合$E_G$に写像$f$を適用して得られる辺集合$E_{f(G)}=\lbrace (f(u),f(v))| (u,v)\in E_G\rbrace$がすべてホストグラフの辺集合$E_H$に含まれている,つまり$E_{f(G)}\subseteq E_H$であれば,埋め込み成功です.このとき,グラフ$H$は$GG$を部分グラフとして含みます.埋め込みできない場合は,埋め込みができた辺集合$E_{f(G)}\cap E_H$の要素数を最大化するように埋め込み$f$を求めます.
グラフ埋め込みの解の例
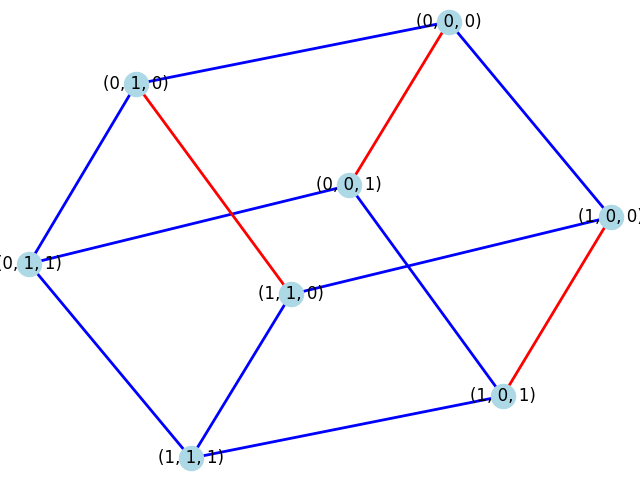
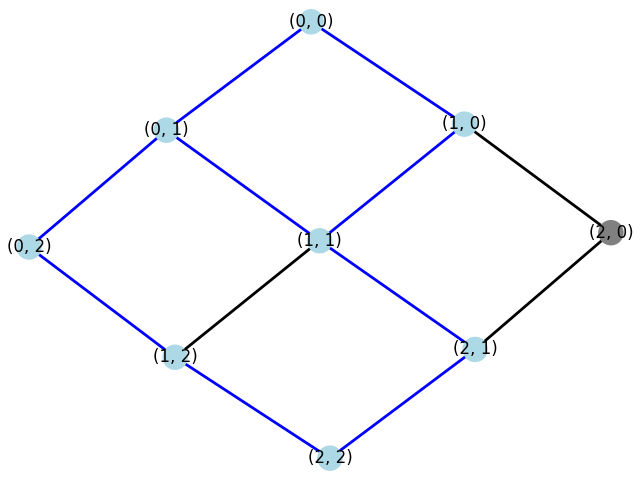
下記の図では,8頂点からなるゲストグラフ$G$を,9頂点のホストグラフ$H$に埋め込む例を示しています.$G$は12辺で構成されており,埋め込みに成功した辺は青色で,失敗した辺は赤色で示されています.$H$では,埋め込みに利用された辺が青色で表示されています.12辺のうち,埋め込みに成功したのは9辺でした.
| ゲストグラフ$G$: $2\times 2 \times 2$のキューブ | ホストグラフ$H$: $3\times 3$のグリッド |
|---|---|
 |
 |
グラフ埋め込み問題のQUBOへの変換
ゲストグラフ$G=(V_G,E_G)$とホストグラフ$H=(V_H,E_H)$において,QUBOのバイナリ変数の集合$X$を以下のように定義します.
$$
X=\lbrace x_{u,v} | u\in V_G, v\in V_H\rbrace
$$
ここで,埋め込みを示す写像$f:V_G\rightarrow V_H$が$f(u)=v$を満たす場合,$x_{u,v}=1$となるようにQUBOを設計します.
まず,任意の$u\in V_G$に対して,$f(u)$が一意に定まるためように,以下の式を用います.
$$
\sum_{v\in V_H} x_{u,v} =1
$$
さらに,すべての$v\in V_H$について,$f(u)=v$となる$u$が存在しないか,1つだけ存在するため,次の式を満たす必要があります.
$$
\sum_{u\in V_G} x_{u,v} = 0 \quad または \quad 1
$$
前者はone-hot制約1,後者はzero-one-hot制約1を満たすように,QUBOの式を以下のように設定します.
$$
C(X)=\sum_{u\in V_G}(1-\sum_{v\in V_H} x_{u,v})^2+\sum_{v\in V_H}(1-\sum_{u\in V_G} x_{u,v})\sum_{u\in V_G}x_{u,v}
$$
$C(X)$が最小値0を取る場合,$X=(x_{u,v})$は上記の制約をそれぞれ満たし,$x_{u,v}=1$は$f(u)=v$を示します.
次に、成功した埋め込みの辺の総数を計算するQUBOを構築します.$E_G$と$E_H$からそれぞれ一つずつ辺を取り,$(u,u')\in E_G$,$(v,v')\in E_H$とします.埋め込み$f$が$f(u)=v$かつ$f(u')=v'$,または$f(u)=v'$かつ$f(u')=v$を満たす場合,辺$(u,u')$は$(v,v')$に埋め込まれています.したがって,埋め込まれた辺の総数は次の式で算出されます.
$$
E(X)=\sum_{(u,u')\in E_G}\sum_{(v,v')\in E_H} (x_{u,v}x_{u',v'}+x_{u,v'}x_{u',v})
$$
最終的に,$C(X)$が最小値0を取り,かつ$E(X)$が最大値を取るようにQUBOを設定します.
$$
P\cdot C(X)-E(X)
$$
ここで,$P$は$C(X)$を$E(X)$より優先するための係数で,ゲストグラフ$G$の頂点数,つまり$P=|V_G|$とすれば十分です.
Pythonプログラム
ホストグラフ$G$とゲストグラフ$H$は、NetworkXの無向グラフとしてそれぞれhostとguestに指定されます.この例では,guestには$2\times 2 \times 2$のキューブ,hostには$3\times 3$のグリッドが設定されていますが,これらを変更することで,異なるグラフの埋め込み問題を解くことが可能です.
関数embedding_quboは、PyQUBOを使用して$P\cdot C(X)-E(X)$の式をformulaとして構築し、これを展開してQUBO形式のquboに変換します。このquboには定数項が含まれず、定数項はoffsetとして別途保持されます。コード中では、guest_1+host_01が$C(X)$を表し、matchは$-E(X)$に相当します。
関数gurobiは、quboの解solutionを求めます.varsは、キーとしてタプル$(u,v)$の文字列を持ち、値として$x_{u,v}$の値を持つ辞書です.quboをGurobiの目的関数に適合する形式でobjに変換しています.定数項offsetとゲストグラフの辺の数len(guest.edges)の合計に対応するマイナスの値を持つ解が見つかった場合,解探索を即座に終了させるためのコールバック関数mycallbackを設定しています.この条件が満たされた場合,すべてのゲストグラフの辺が埋め込みに成功していることになります.
辞書mappingは,キーとして$u$,値として$f(u)$を持ち,solutionから導出されます.
$x_{u,v}=1$のときに、キー$u$に対する値として$v$が割り当てられます.
関数print_embeddingは,solutionをわかりやすくテキスト表示するためのもので、draw_embedding関数はmatplotlibを利用して、guestからhostへの埋め込み結果を視覚的に描画し,画像ファイルに保存します.
#!/usr/bin/env python3
import argparse
import networkx as nx
import matplotlib.pyplot as plt
import pyqubo as pq
import gurobipy as gp
import ast
# generate a QUBO model for embedding guest graph in host graph
def embedding_qubo(guest, host):
pairs = [(v_g, v_h) for v_h in host.nodes for v_g in guest.nodes]
vars = {p: pq.Binary(str(p)) for p in pairs}
host2guest = [[vars[(v_g, v_h)] for v_g in guest.nodes] for v_h in host.nodes]
guest2host = [[vars[(v_g, v_h)] for v_h in host.nodes] for v_g in guest.nodes]
host_01 = sum([sum(p) * (sum(p) - 1) for p in host2guest])
guest_1 = sum([(sum(p) - 1) ** 2 for p in guest2host])
match = sum(
[
-vars[(e_g[0], e_h[0])] * vars[(e_g[1], e_h[1])]
- vars[(e_g[0], e_h[1])] * vars[(e_g[1], e_h[0])]
for e_h in host.edges
for e_g in guest.edges
]
)
formula = match + len(guest.nodes) * host_01 + len(guest.nodes) * guest_1
model = formula.compile()
qubo, offset = model.to_qubo()
return qubo, int(offset)
# Gurobi call back function: terminate if all guest edges are embedded
def mycallback(model, where):
if where == gp.GRB.Callback.MIPSOL:
if int(model.cbGet(gp.GRB.Callback.MIPSOL_OBJ)) == qubo_optimal:
model.terminate()
# Find solution of qubo using Gurobi
def gurobi(qubo, timelimit):
model = gp.Model()
model.setParam("TimeLimit", timelimit)
vars = {}
for v in list((v for tup in qubo for v in tup)):
vars[v] = model.addVar(vtype=gp.GRB.BINARY, name=v)
obj = [val * vars[key[0]] * vars[key[1]] for key, val in qubo.items()]
model.setObjective(gp.quicksum(obj), sense=gp.GRB.MINIMIZE)
model.optimize(mycallback)
solution = {key: int(val.X) for key, val in vars.items()}
return solution, int(model.ObjVal)
# Display embedding result
def print_embedding(guest, host, mapping):
print("Node mapping: guest to host")
for key, val in sorted(mapping.items()):
print(key, ":", val)
print("Edge mapping: guest to host")
for u, v in guest.edges:
if (mapping[u], mapping[v]) in host.edges:
print((u, v), ":", (mapping[u], mapping[v]))
else:
print((u, v), ": failure")
# Draw embedding
def draw_embedding(guest, host, mapping, guest_file, host_file):
combined = nx.Graph()
combined.add_edges_from([(mapping[u], mapping[v]) for u, v in guest.edges])
edge_color = ["blue" if e_h in combined.edges else "black" for e_h in host.edges]
node_color = [
"lightblue" if v_h in mapping.values() else "gray" for v_h in host.nodes
]
pos = nx.spring_layout(host)
nx.draw(
host,
pos,
with_labels=True,
node_color=node_color,
edge_color=edge_color,
width=2,
)
plt.savefig(host_file)
plt.clf()
edge_color = [
"blue" if (mapping[u], mapping[v]) in host.edges else "red"
for u, v in guest.edges
]
pos = nx.spring_layout(host)
plt.clf()
nx.draw(
guest,
with_labels=True,
node_color="lightblue",
edge_color=edge_color,
width=2,
)
plt.savefig(guest_file)
def main():
global qubo_optimal
parser = argparse.ArgumentParser(
description="Embedding a guest graph in a host graph using Pyqubo and Gurobi"
)
parser.add_argument(
"-t", "--timelimit", default=30, type=int, help="Gurobi Timelimit"
)
parser.add_argument(
"--guest", default="guest.png", type=str, help="File for drawing guest graph"
)
parser.add_argument(
"--host", default="host.png", type=str, help="File for drawing host graph"
)
args = parser.parse_args()
host = nx.grid_graph([3, 3]) # host graph
guest = nx.grid_graph([2, 2, 2]) # guest graph to be embedded
qubo, offset = embedding_qubo(guest, host) # generate QUBO for embedding
qubo_optimal = -len(guest.edges) - offset # optimal QUBO energy if all guest edge
solution, objval = gurobi(qubo, args.timelimit) # Find solution using Gurobi
mapping = { # Find guest to host node mapping from solution
ast.literal_eval(key)[0]: ast.literal_eval(key)[1]
for key, val in solution.items()
if val == 1
}
print_embedding(guest, host, mapping) # display obtained embedding
draw_embedding(guest, host, mapping, args.guest, args.host) # draw embedding
print(f"optimal = {-len(guest.edges)} obtained = {offset+objval}")
if __name__ == "__main__":
main()
実行結果
先のPythonプログラムの実行結果です.ゲストグラフ$G$のノードは,$(i,j,k)$ ($0\leq i,j,k\leq 1$)で表され,ホストグラフ$H$のノードは$(i,j)$ ($0\leq i,j\leq 2$)で表されています.ゲストグラフ$G$のうち3つの辺の埋め込みが失敗しています.Gurobiはこの解がBoundと一致する最適解で,より良い埋め込みは存在しないことを示しています.
Node mapping: guest to host
(0, 0, 0) : (2, 2)
(0, 0, 1) : (1, 0)
(0, 1, 0) : (2, 1)
(0, 1, 1) : (1, 1)
(1, 0, 0) : (1, 2)
(1, 0, 1) : (0, 0)
(1, 1, 0) : (0, 2)
(1, 1, 1) : (0, 1)
Edge mapping: guest to host
((0, 0, 0), (1, 0, 0)) : ((2, 2), (1, 2))
((0, 0, 0), (0, 1, 0)) : ((2, 2), (2, 1))
((0, 0, 0), (0, 0, 1)) : failure
((0, 0, 1), (1, 0, 1)) : ((1, 0), (0, 0))
((0, 0, 1), (0, 1, 1)) : ((1, 0), (1, 1))
((0, 1, 0), (1, 1, 0)) : failure
((0, 1, 0), (0, 1, 1)) : ((2, 1), (1, 1))
((0, 1, 1), (1, 1, 1)) : ((1, 1), (0, 1))
((1, 0, 0), (1, 1, 0)) : ((1, 2), (0, 2))
((1, 0, 0), (1, 0, 1)) : failure
((1, 0, 1), (1, 1, 1)) : ((0, 0), (0, 1))
((1, 1, 0), (1, 1, 1)) : ((0, 2), (0, 1))
optimal = -12 obtained = -9